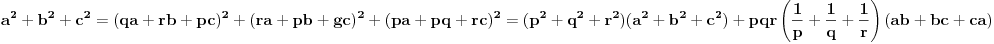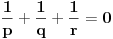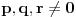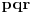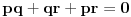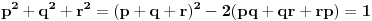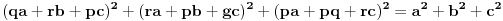[ edisnp @ 30.12.2010. 20:36 ] @
| Zadatak je sledeci:Neka su p,q,r realni brojevi za koje vazi 1/p+1/q+1/r=0 i p+q+r=1.Dokazati da za sve realne brojeve a,b,c vazi: a^2+b^2+c^2=(qa+rb+pc)^2+(ra+pb +gc)^2+(pa+pq+rc)^2. Neznam kako se ovakva vrsta zadataka resava, nesto sam pokusao da uradim: pq+qr+pr=0 odatle je r(p+q)+pq=0 ,p+q =1-r i sad zamenom dobijemo r-r^2+qp=0 a, p=1-q-r i opet zamenom dobijemo:r(1-r-q)+q(1-q) =0 to izjednacimo sa pr+qr+pq i iz toga zakljucujemo da nam je r razlicito od q i dobijemo da nam je q=2-2p-r/3 i sad ne znam sta dalje da radim.Bio bi mi potreban neki metod kako se ovo resava.k |