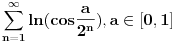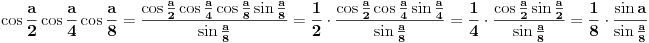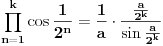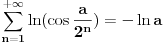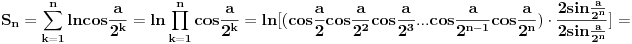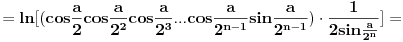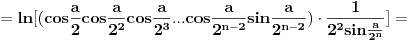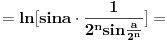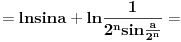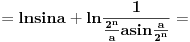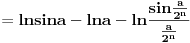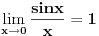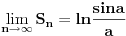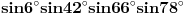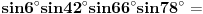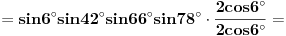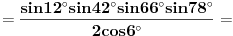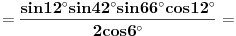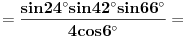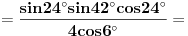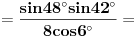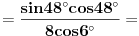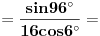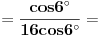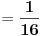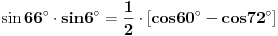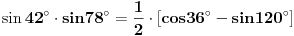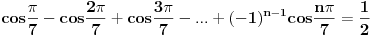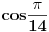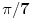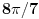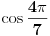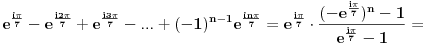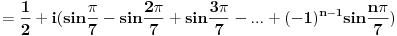[ petarm @ 01.01.2011. 21:19 ] @
|
[ petarm @ 01.01.2011. 23:07 ] @
[ petarm @ 01.01.2011. 23:21 ] @
[ petarm @ 01.01.2011. 23:45 ] @
[ Fermion @ 02.01.2011. 01:37 ] @
[ petarm @ 16.01.2011. 00:44 ] @
[ Nedeljko @ 16.01.2011. 10:20 ] @
Ništa strašno. To su brojevi kongruentni sa 3 po modulu 7.
[ petarm @ 16.01.2011. 11:24 ] @
[ Nedeljko @ 16.01.2011. 11:44 ] @
[ petarm @ 16.01.2011. 12:05 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|