[ yoMas @ 02.01.2011. 18:16 ] @
| Odrediti najmanji prirodan broj cija je polovina potpun kvadrat, trecina potpun kub i petina potpun peti stepen. [Ovu poruku je menjao yoMas dana 02.01.2011. u 20:10 GMT+1] |
|
[ yoMas @ 02.01.2011. 18:16 ] @
[ Nedeljko @ 02.01.2011. 19:18 ] @
Dakle, taj broj se može prikazati u obliku
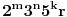 , gde , gde  nije deljivo ni sa 2 ni sa 3 ni sa 5. nije deljivo ni sa 2 ni sa 3 ni sa 5.Pošto broj mora biti deljiv sa 2, 3 i 5, imamo da je 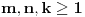 . .Iz prvog uslova sledi da 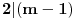 , , 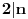 , , 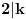 i da je i da je  potpun kvadrat. potpun kvadrat.Iz drugog uslova sledi da 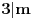 , , 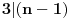 , , 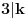 i da je i da je  potpun kub. potpun kub.Iz trećeg uslova sledi da 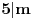 , , 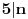 , , 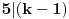 i da je i da je  potpun peti stepen. potpun peti stepen.Pošto tražimo najmanji takav broj, uzimamo da je 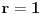 . .Na način objašnjen u ovoj temi, dobija se da se najmanje rešenje dobija za 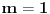 , , 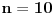 i i 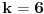 . .Dakle, rešenje je 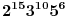 . .[ yoMas @ 02.01.2011. 19:35 ] @
Slicno sam uradila kao i vi :
Neka nam x bude najmanji broj. Pretpostavit cemo da su 2, 3 i 5 su svi glavni. Tada je najmanji mogući broj x i on samo moze imati 2, 3 i 5 kao njezin jedine proste faktore. Neka je x= 2^a 3^b 5^c Stanje 1. x je polovica potpunog kvadrata 2x= 2^a+1 3^b 5^c .. To zahtijeva 2|a+1,b,c Stanje 2. x je jedna trećina od potpunog kuba 3x= 2^a3^b+1 5^c . To zahtijeva 3|a,b+1,c Stanje 3. x je jedna petina petine stepena 5x= 2^a 3^b 5^c+1 . To zahtijeva 5|a,b,c+1.. Mi ćemo ispitati svaku varijablu (a,b i c) jedan po jedan. Za a, imamo 2|a+1 što znači je neparan. Onda 3,5|a znači da 15|a. Iz toga slijedi da je. Min(a)=15 Za b, imamo 2,5|b a to podrazumijeva da 10|b. 3|b+1 znači b=2(mod 3) . minimum b koji zadovoljava taj uvjet je 20. Za c, imamo 2,3|c a to podrazumijeva da 6|c. 5|c+1. Znači c=4(mod 5).. minimum c koji zadovoljava taj uvjet je 24. Stoga željeni broj je 2^a3^b5^c . sto je i trebalo dokazati. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|