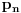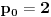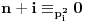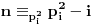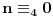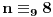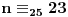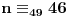[ Mortifera @ 02.01.2011. 19:57 ] @
|
| Imam jedan zadatak koji je dosta blizak zadacima iz teorije brojeva, pa glasi:
...dokazati da postoji k uzastopnih prirodnih brojeva od kojih je svaki deljiv sa kvadratom prirodnog broja veceg od 1...
Da li ima ko predstavu kako da se resi ovaj zadatak? |
[ Nedeljko @ 02.01.2011. 20:09 ] @
Opet sistem kongruencija.
Dakle, n je kongruentno nuli po modulu 4, n+1 je kongruentno nuli po modulu 9, n+2 je kongruentno nuli po modulu 16,..., n+k-1 je kongruentno nuli po modulu (k+1)2.
Drugim rečima,
n je kongruentno sa (i+2)2-i po modulu (i+2)2 za i=0,...,k-1.
Takav broj postoji po kineskoj teoremi o ostacima.
[ Mortifera @ 02.01.2011. 20:18 ] @
Hmm...ideja mi je jasna, tj namera, ali kako da dokazem da taj broj postoji po kineskoj teoremi o ostacima?
Znam kako glasi i kako se dokazuje Teorem o CRT-u, ak kako bih primenio na ovaj broj?
[ Nedeljko @ 02.01.2011. 20:23 ] @
Pardon, CRT zahteva da su moduli u parovima uzajamno prosti, pa za module treba uzeti kvadrate prvih k prostih brojeva.
Ako je
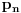
rastući niz svih prostih brojeva,
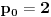
, onda treba da za

bude
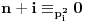
, odnosno
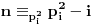
.
[ Nedeljko @ 02.01.2011. 20:29 ] @
[ Mortifera @ 02.01.2011. 20:41 ] @
Svidja mi se pristup...Znaci, trebao bih da u ovom zadatku navedem CRT teoremu, da je iskazem i dokazem, te da se pozivam na nju, i da raspisem ovo sto ste mi Vi napisali?
[ Nedeljko @ 02.01.2011. 21:17 ] @
Ako je ispit ili domaći u pitanju, valjda imaš pravo da se pozoveš na sve teoreme koje ste učili.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.