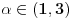U okolini beskonačnosti je podintegralna funkcija asimptotski ekvivalentna sa , odakle sledi da mora biti . U okolini nule je asimptotski ekvivalentna sa , odakle sledi da mora biti . Obzirom da drugih singulariteta nema. .

Nedjeljko, izvini znam da je pitanje pomalo "naivno" al koji je ovo kriterij...

Poredbeni, valjda.

Nisam siguran kako si ovo dobio preko poredbenog? Ja sam ocekivao kriterijum "ponasa se kao". Ako se tako zove? Nazivi i nisu toliko bitni!

Poredbeni je koliko znam da umesto funkcije koristis , a pri tome koristis

na tom intervalu integracije npr.

Kriterijum "ponasa se kao"




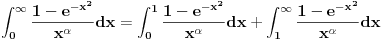
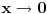
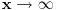
Sada posmatramo singularitete. To su u prvom integralu s desne strane jednakosti i u drugom integralu s desne strane jednakosti. Obelezimo integrand sa . Dakle,

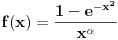
Sada treba videti kako se ovaj integrand ponasa kada, u prvom slucaju,





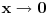
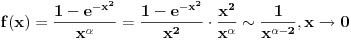
jer je

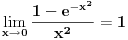
- primeni se Lopitalovo pravilo

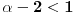
Dakle, prvi integral s desne strane konvergira za tj.







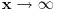
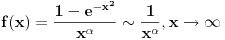
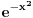
E ovde se mozda moze reci da je u pitanju uporedni kriterijum jer je zanemarljivo u odnosu na .

Drugi integral konvergira za

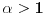
pa se dobija da integral s leve strane, tj. nas pocetni integral, konvergira za

Bilo bi interesantno sada formulisati ovakav problem. Ovo vec nije trivijalno!

ZAD
Naci vrednost nesvojstvenog integrala



za one kada on konvergira.

Uspeo sam da izguram resenje primenom Laplasove transformacije. Bez ne znam kako bih. Ako neko ima ideju voleo bih da je vidim?

RES:



smena:



tj.







U ovom slucaju , a i jos treba uracunati ispred integrala



Treba sad samo videti sta je u nasem slucaju ?



smena:














pa je



odnosno



u slucaju kada ovaj integral konvergira!

Nadam se da nisam negde zeznuo. Resenje zavisi od sto ima smisla :) Ipak malo je dugacko. Ako neko ima ideju za neko elegantnije resenje neka postuje. Ovo je vise drljacko resenje :D

Moglo je i direktno da se svede na Gama funkciju. Laplasovom transformacijom sam se igrao zbog praznickog raspolozenja i da jos malo zakukuljim resenje :D

Kraca varijanta je

RES:




Bilo bi zanimljivo videti neko alternativno resenje!

_{[Ovu poruku je menjao petarm dana 05.01.2011. u 20:29 GMT+1]}