|
|
[ different @ 04.01.2011. 11:59 ] @
|
| Dat je skup A={1,2,3,4,5,6,7,8,9}. Odrediti relaciji ρ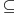 AxA takva da je XρY AxA takva da je XρY X≤Y X≤Y
i osobine te realacije.
Razumije li ko od vas ovaj zadatak???
|
[ petarm @ 04.01.2011. 13:21 ] @
Davno sam bas radio relacije. Tako da nisam siguran da li sam u pravu. Ali koliko se secam ovo bi trebalo da bude skup uredjenih dvojki tako da prvi broj u uredjenoj dvojci mora biti manji ili jednak od drugog.
[ edisnp @ 04.01.2011. 13:57 ] @
Dekartov kvadrat skupa A je A^2=AxA={(a.b)| a,b elemenat}
A={1,2,3,4,5,6,7,8,9}
AxA={(1.1),(1.2),(1.3),(1.4),(1.5),(1.6),(1.7),(1.8),(1.8),(1.9),,(2.2),(2.3),(2.4),(2.5),(2.6),(2.7),(2.8),(2.9),
,,(3.3),(3.4),(3.5),(3.6),(3.7),(3.8),(3.9),,(4.4),(4.5),(4.6),(4.7),(4.8),(4.9),,(5.5),(5.6),(5.7),(5.8),(5.9),(6.6),(6.7),(6.8),(6.9)(7.7),(7.8),(7.9),(8.8),(8.9),(9.9)} ovo su svi podskupovi dekartovog proizvoda nepraznih skupova relacija je refleksivna .
[ Fermion @ 04.01.2011. 14:38 ] @
I ja sa relacijama i skupovima nisam nešto dugo radio, osim malo zadnji put na nekoj temi ovde na forumu, ali mislim da se Dekartov proizvod skupova formira ovde tako što najpre razmatraš sve moguće rasporede (x,y) za vrednosti x,y koje uzimaš iz skupa A, ali po uslovu zadatka tako da 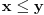 .
Pa tako imaš skup A={1,2,3,4,5,6,7,8,9} treba da biraš parove brojeva iz ovog skupa tako da je prvi manji ili jednak drugom. I to je valjda ono što je edisnp napisao. [ Fermion @ 04.01.2011. 14:53 ] @
A za osobine...
Jeste refleksivna, jer svaki element je u relaciji sa samim sobom (1,1), (2,2),...,(9,9).
Nije simetrična, jer bi za svako x,y tada moralo biti, ako je x u relaciji sa y onda je i y u relaciji sa x. Jasno da je naprimer (1,9), a ne i (9,1).
Antisimetrična je ako je za svako x,y za koje je x u relaciji sa y i y u relaciji sa x sledi da je x=y. Prema tome ovo je antisimetrično (1,1), (2,2), ...
Tranzitivnost bi značila da se za svako x, y, z za koje je x u relaciji sa y i y u relaciji sa z važi da je x u relaciji sa z. Ovo bi ovde značilo ako je 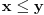 i 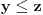 , sledi da je 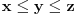 što se svodi na 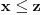 , pa je i x u relaciji sa z.
Prema tome relacija je refleksivna, antisimetrična i tranzitivna.
Valjda :). [ edisnp @ 04.01.2011. 15:54 ] @
Ne bi trebalo da je antisimetricna jer svako x koje je u relaciji sa y
nije svako y relaciji x i x nije jednako y.Ono na primer jeste kod
slucaja (1.1) ili (2.2) ali kada je na primer (4.9) onda x nije jednako y
tj. slucaja (4.9) zadovoljava uslov da je x manje od y odnosno y je vece od x
sto zadovoljava relaciju ali x nije jednako y.
[ Fermion @ 04.01.2011. 16:28 ] @
Definicija antisimetričnosti je:
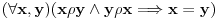
To znači da za svako x, y za koje je x u relaciji sa y i y u relaciji sa x sledi da je 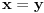 .
U tvom primeru 4 jeste u relaciji sa 9 ( 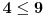 ), ali 9 nije u relaciji sa 4 (ne važi 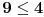 ).
Ako je 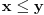 i 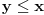 sledi da je 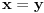 , pa je relacija antisimetrična. [ Fermion @ 04.01.2011. 16:52 ] @
Uostalom, ovo je relacija poretka pa je refleksivna, antisimetrična i tranzitivna.
[ edisnp @ 04.01.2011. 17:54 ] @
Da ,jer je relacija poretka svaka relacija koja ima osobine R,AS,T.Da nema osobinu
antisimetricnosti a ima osobinu simetricnosti onda bi bila relacija EKVIVALENCIJE.
[ different @ 05.01.2011. 06:36 ] @
A sta je zadatak bio postavljen tako da je umjesto ralacije  bila relacija  , tj.da je zadatak glasio na sledeci nacin.
Dat je skup A={1,2,3,4,5,6,7,8,9}. Odrediti relaciji ρ 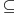 AxA takva da je XρY  X≤Y
i osobine te realacije.
Kako bi se u tom slucaju uradio zadatak. [ Sini82 @ 05.01.2011. 11:46 ] @
U tom slučaju, relacija  , bila bi podskup relacije 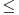 . Tada bi rješenja bila svi elementi partitivnog skupa skupa uređenih parova relacije 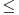 . Rješenje ne bi bilo jedinstveno, svaki element partitivnog skupa bio bi jedna relacija. Analizirali bi osobine svake relacije posebno zavisno od toga koji od podskupova posmatramo.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|