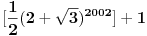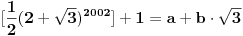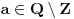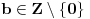[ Fermion @ 06.01.2011. 13:40 ] @
|
[ Sini82 @ 06.01.2011. 22:57 ] @
[ Fermion @ 06.01.2011. 23:14 ] @
U zadatku to nije naglašeno, ali koliko sam ja shvatio [...] označava ceo deo, a ne zagradu pa je broj iz skupa prirodnih.
[ petarm @ 07.01.2011. 17:01 ] @
[ Sini82 @ 07.01.2011. 18:18 ] @
Citat: Fermion: U zadatku to nije naglašeno, ali koliko sam ja shvatio [...] označava ceo deo, a ne zagradu pa je broj iz skupa prirodnih. Uglasta zagrada [...] nije oznaka za cijeli dio. Oznake su drugačije, za donji cijeli dio  (zaokružuje na manju cjelobrojnu vrijednost) i gornji cijeli dio (zaokružuje na manju cjelobrojnu vrijednost) i gornji cijeli dio  (zaokružuje na veću cjelobrojnu vrijednost). Koje oznake treba koristiti u zadatku? (zaokružuje na veću cjelobrojnu vrijednost). Koje oznake treba koristiti u zadatku?[ Fermion @ 07.01.2011. 18:39 ] @
Ja sam uvek koristio oznaku [] za celi deo, a {} za ono decimalno...
U knjizi je dat izraz u tačno takvom obliku kakvim sam ga ja ovde postavio. Obična uglasta zagrada. I misli se na ceo deo koliko sam shvatio po rešenju. Uostalom da je ovo zagrada bila pi potpuno suvišna. [ petarm @ 07.01.2011. 19:09 ] @
Ja sam koristio tu oznaku
 cesto na Analizi 1 kod resavanja limesa po definiciji. Posto je cesto na Analizi 1 kod resavanja limesa po definiciji. Posto je 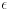 realno tamo u definiciji, a realno tamo u definiciji, a  prirodno, a biramo prirodno, a biramo  u nekoj funkciji od najveceg celog dela od neke funkcije epsilona i dodamo u nekoj funkciji od najveceg celog dela od neke funkcije epsilona i dodamo  npr. Te oznake koje Sini je napisao sigurno imaju veoma mnogo smisla kad baratas i sa najvecim celim i najmanjim celim delom od necega. U slucaju da je potreban samo najveci ceo stavim prosto npr. Te oznake koje Sini je napisao sigurno imaju veoma mnogo smisla kad baratas i sa najvecim celim i najmanjim celim delom od necega. U slucaju da je potreban samo najveci ceo stavim prosto 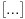 . Ja mislim da je ovde u zadatku najveci ceo deo od tog izraza. Jer zadatak ne bi imao smisla inace. . Ja mislim da je ovde u zadatku najveci ceo deo od tog izraza. Jer zadatak ne bi imao smisla inace. [ Fermion @ 07.01.2011. 19:26 ] @
Da, ovo u zadatku je sigurno ceo deo. Tačnije najveći celi broj manji od onog u zagradi. Odredio sam to i na osnovu rešenja. Ali tamo koriste rekurentne jednačine, ja bih hteo bez toga.
[ Farenhajt @ 07.01.2011. 19:30 ] @
[ Fermion @ 07.01.2011. 19:37 ] @
Citat: Farenhajt: Da li se njihovo rešenje svodi na uočavanje da je 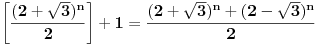 ? ?Da. Posle se postupak malo razlikuje, ali to je glavna ideja. Saću da prepričam rešenje, ali kao što rekoh, mene interesuje da li postoji neko drugo bez rekurentnih jednačina. [ Fermion @ 07.01.2011. 21:13 ] @
Evo kako sam ja razumeo njihovo rešenje:
Označimo 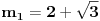 , , 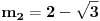 . .Nađimo kvadratnu jednačinu čija su rešenja 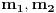 . Posto je: . Posto je: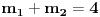 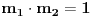 Iz Vietovih veza: 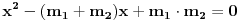 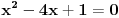 Ovo je karakteristični polinom za linearnu rekurentnu jednačinu: 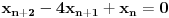 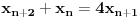 Pomeranjem indeksa: 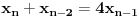 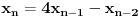 Rešenje ove jednačine je: 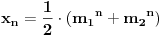 Sama rekurentna veza naravno ima smisla za 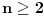 da ne bismo imali negativan indeks. da ne bismo imali negativan indeks.Za n=0 i n=1 izračunaćemo vrednost  prostom zamenom u rekurentnu vezu. prostom zamenom u rekurentnu vezu.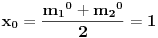 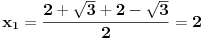 Koristeći vezu 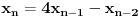 lako izračunavamo prve članove za lako izračunavamo prve članove za 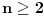 . .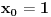 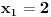 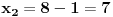 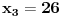 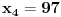 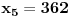 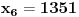 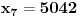 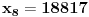 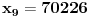 Ostatak pri deljenju broja  sa 7 obeležićemo sa sa 7 obeležićemo sa 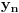 . .Ti ostaci iznose: 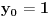 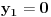 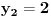 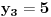 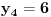 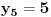 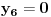 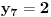 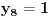 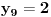 S obzirom da postoji ponavljanje članova, odnosno 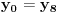 i i 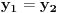 zaključujemo da je niz ostataka zaključujemo da je niz ostataka 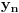 periodičan sa periodom 8. periodičan sa periodom 8.To znači da je 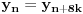 . S obzirom da je . S obzirom da je 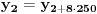 sledi da je sledi da je 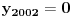 . .Posto je broj 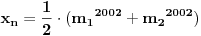 , a , a 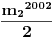 leži u intervalu leži u intervalu  , tj. , tj. 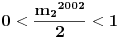 , sledi , sledi 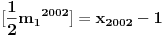 . Pošto je . Pošto je 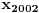 deljivo sa 7, sledi da je ostatak pri deljenju celog dela iz polaznog oblika jeste 6, ali pošto se na njega dodaje 1 dobija se oblik deljiv sa 7. deljivo sa 7, sledi da je ostatak pri deljenju celog dela iz polaznog oblika jeste 6, ali pošto se na njega dodaje 1 dobija se oblik deljiv sa 7.E sad, ja sam njihovo rešenje koje je stalo na 8 redova u knjizi, prilično interpretirao, pa je ispalo ovakvo dugačko, eventualne greške su sigurno moje :). Nisam koristio ni uvek iste oznake. Ipak suština je u rekurentnim vezama i periodičnosti onih ostataka. Zadatak sam inače našao knjizi "Uvod u teoriju brojeva", (sveska 15 iz "Materijala za mlade matematičare), na strani 9, zadatak 38, sa već pomenutog takmičenja, autori knjige su Vladimir Mićić, Zoran Kadelburg i Dušan Đukić. Eto, pa ako imate neke ideje kako ovo da se uradi bez rekurentnih veza iznesite ih. [Ovu poruku je menjao Fermion dana 07.01.2011. u 22:47 GMT+1] [Ovu poruku je menjao Fermion dana 07.01.2011. u 23:23 GMT+1] [ Fermion @ 07.01.2011. 22:07 ] @
Citat: Farenhajt: Da li se njihovo rešenje svodi na uočavanje da je 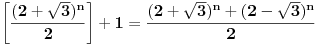 ? ?U tom slučaju se za 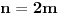 dobija dobija 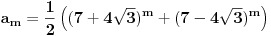 , pa je rekurentna veza , pa je rekurentna veza 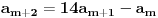 . Shodno tome, svi neparno indeksirani članovi niza daju istu apsolutnu vrednost ostatka pri deljenju sa . Shodno tome, svi neparno indeksirani članovi niza daju istu apsolutnu vrednost ostatka pri deljenju sa 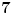 , a kako je , a kako je 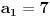 , zaključak za , zaključak za 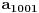 sledi. sledi.Sad da razjasnim u kom smislu se svodi na: 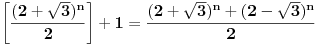 Na kraju onog rešenja se u jednom koraku dobije: 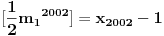 Ovo je naravno ekvivalentno sa pomenutom jednakošću. Mada mi nije jasno kako doći do nje bez toliko dugačkog postupka kakav sam izložio, moram reći - svaka čast na opažanju. Sjajno rešenje. [ Fermion @ 08.01.2011. 21:42 ] @
Citat: petarm: Evo jednog zabavnog zadatka ZAD Dat je izraz 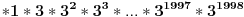 Sava i Vlada naizmenicno zamenjuju po jednu zvezdicu sa 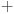 ili ili  . Vlada nastoji da broj koji se dobije, posle zamene i poslednje zvezdice, bude deljiv sa . Vlada nastoji da broj koji se dobije, posle zamene i poslednje zvezdice, bude deljiv sa 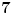 . Moze li Sava da ga spreci u tome ako on igra prvi? . Moze li Sava da ga spreci u tome ako on igra prvi?Može Evo i kako. Prvo primetimo da je 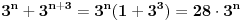 To znači da je 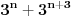 deljivo sa 7 za deljivo sa 7 za 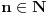 . .Najpre Sava treba pored jedinice da stavi + ili -. Na svaku Vladinu izmenu Sava mora da upotrebi isti znak, i da ga stavi uz trojku čiji je eksponent veći ili manji za tri od eksponenta broja koji je Vlada odabrao. Na taj način će se stalno dobijati vrednost 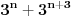 za različito n, s tim što je predznak uz nju + ili -, ali jasno da je u tom slučaju takav broj deljiv sa 7. Pošto imamo 1998 stepena broja tri možemo ih organizovati u takve parove. za različito n, s tim što je predznak uz nju + ili -, ali jasno da je u tom slučaju takav broj deljiv sa 7. Pošto imamo 1998 stepena broja tri možemo ih organizovati u takve parove.Pošto će se tako stalno dobijati parovi deljivi sa 7, njihova suma će isto tako biti deljiva sa 7. Ipak ostaje na kraju ona jedinica ispred koje je Sava stavio odgovarajući znak u prvom potezu, pa će broj biti kongruentan 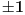 po modulu 7, tj. neće biti deljiv brojem 7. po modulu 7, tj. neće biti deljiv brojem 7.Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|