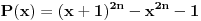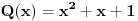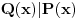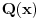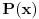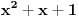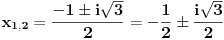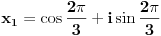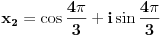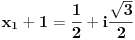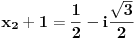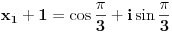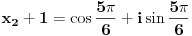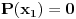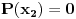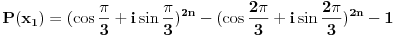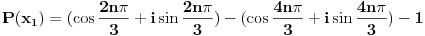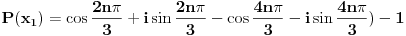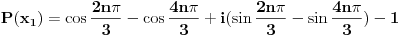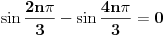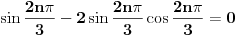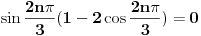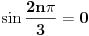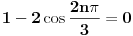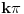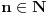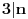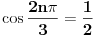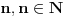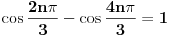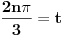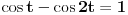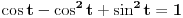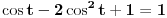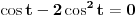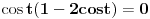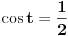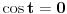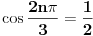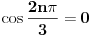Neka je:



Pretpostavimo da je . Tada su nule polinoma ujedno i nule polinoma .

Dakle dovoljno je rešavanjem kvadratne jednačine naći njena dva korena i ubaciti vrednosti dobijene za x u:


Zatim treba razmotriti slučajeve kada je n parno i kada je neparno. Pošto se u oba slučaja ne dobije nula pomoću oba korena, zaključujemo da predpostavka nije ispunjena i da Q(x) nije delilac P(x).

Nisam radio ovaj zadatak, samo sam opisao princip kojim se može rešiti.

Predpostavimo suprotno, tj. da je polinom P(x) deljiv polinom Q(x).

Nule polinoma Q(x) tada su i nule polinoma P(x).

Nađimo te nule:










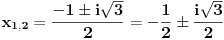
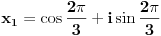
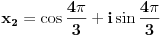
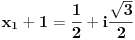
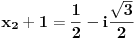
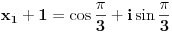
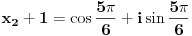
Da bi polinom P(x) bio deljiv sa Q(x) potrebno je i dovoljno da:

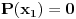
i

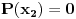
Korišćenjem Moavrove formule:






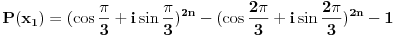
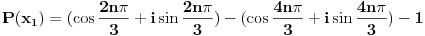
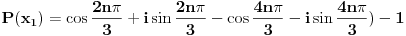
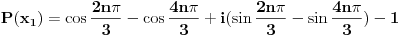
Da bi ovo bilo nula imaginarni deo isto mora biti nula.





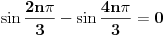
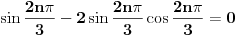
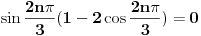
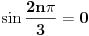
Imamo odatle da ili je ili .

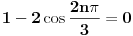
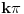
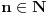
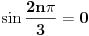
S obzirom da su nule sinusne funkcije oblika , a sledi da ako je tada .

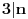
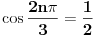
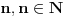
Treba ispitati kada za gde n nije deljivo sa 3.

Za takve n zatim rešiti jednačinu:


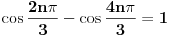
da bi .
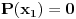
Uvedimo smenu:






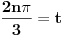
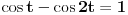
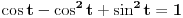
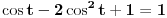
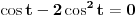
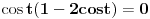
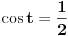
Prema tome ili je ili

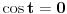
Odnosno:
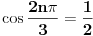
ili .

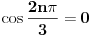
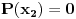
Da dalje ne bih pisao, preobimno je, odredi se za koje n ovo može da važi, i za takvo n na potpuno analogan način ispita, da li je moguće da bude za takvo n, pa onda ako se dobije da nije, onda je predpostvka pogrešna i P(x) nije deljivo sa Q(x).

P.S. Mogao sam i pogrešiti jer sam kucao bez pisanja na papir, ali uglavnom ideja bi trebala da bude tačna.


_{[Ovu poruku je menjao Fermion dana 07.01.2011. u 20:02 GMT+1]}

@Fermion hvala puno si mi pomogao,,, bitna mi je bila ideja,,,