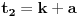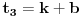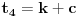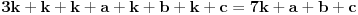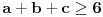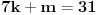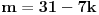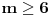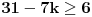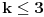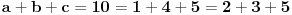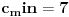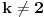4+5+6+7+12=34>33, pa je na prvoj godini položio manje od 4 ispita
2+3+4+5+6=20<33, pa je na prvoj godini položio više od 2 ispita.

Dakle, na prvoj godini je položio 3, a na petoj 9 ispita. Na preostale tri godine je položio 19 ispita.

7+6+5=18<19, pa je na četvrtoj godini položio više od 7 ispita, ali manje nego na 9.

Znači, na četvrtoj godini je položio 8 ispita. Na preostale dve godine je položio 11 ispita.

Rešenja su 3+4+7+8+9=31 i 3+5+6+8+9=31.

Neka je položio k ispita u prvoj. Onda je u petoj položio 3k, a u drugoj, trećoj i četvrtoj, redom:




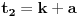
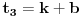
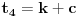
Suma toga je:




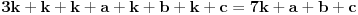
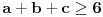
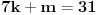
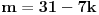
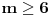
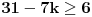
Jasno da je i , odnosno da je .

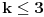
Ako je k=3, onda je m=10. Zadnji član je tad 9, ali 9>3+c, pa je c<6.

c>a>b pa pošto

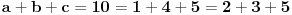
Tako imamo dve mogućnosti:

-U prvoj prvoj položio 3, u drugoj 4, trećoj 7, četvrtoj 8, petoj 9.
-U prvoj prvoj položio 3, u drugoj 5, trećoj 6, četvrtoj 8, petoj 9.

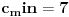
Ako je k<3 onda ako je k=2 m=17, m=a+b+c, a<b<c, pa je , a pošto je tada četvrti član veći ili jednak 10 ne može biti manji od petog koji je 6. Prema tome .

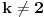
Ako je k=1 to je jasno nemoguće jer bi tad zadnji član bio 3, a između 1 i 3 ne možemo staviti tri različita broja.

Odatle sledi da su izdvojena rešenja jedinstvena.

Nedeljko je bio malo brži sa odgovorom, no dobro, koristiće ti oba rešenja, pogotovo pošto se razlikuju u pristupu :).

Hvala puno obojici.:*:D