Izvinjavam se što nisam imao vremena da se patim sa tex-om, a bilo mi je žao da ti ne odgovorim za ovaj drugi integral jer sam iz prve video rešenje ...

Evo:

I nemoj da se neko smejao rukopisu !

Evo kako bih ja uradio prvi:
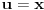
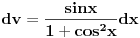
Razdvajanjem na dva integrala i parcijalnom integracijom (, dobija se:

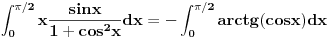
Takodje, skoro analogno za drugi:

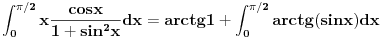
Treba jos primetiti da je zbir ova dva preostala integrala jednak 0,
tako sto u oba rastavimo granice:

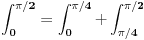
U prvom integralu i prvoj granici uvedes smenu

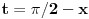
i dobijas da je jednak drugom delu drugog integrala. Analogno za preostala 2 i resenje je


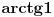
P.S. Ja imam lepsi rukopis;)

Momci, hvala vam puno za ovo!

Ali nije mi bas sasvim jasan ovaj postupak da li bi mogli malo opsirnije da pojasnite, unapred hvala.

Koji od ova dva?

Ovaj deo mi nije jasan, a iz drugog zadatka me interesuje kako je dobio: I=4*integral{x*dx/(3+cos4x)}

Hvala

Ti imas

U prvom sabirku uvedes smenu
Dobija se (samo prvi pisem):

sto je jednako cetvrtom sabirku. Isto uradis i za drugi=>dobijes treci. Primeti kako su granice promenjene uvodjenjem smene i kako je minus nestao izokretanjem granica.

P.S. Ova dva integrala inace mogu da se rese i obicnom integracijom, dobice se isto resenje, ali su jedni od, po meni, komplikovanijih integrala

E, a kako mozes da skratis integral{arctg(cost)} sa integral{arctg(cosx)}, ovaj prvi je sa x a drugi sa t?

Pa ne bi mogao da su neodredjeni, ovako posto su odredjeni, taj integral je zapravo samo neki konacan broj, zar ne?


Ime promenljive uopste nije bitno u celoj prici

Hvala vam puno momci, stvarno ste me izvukli!

da li bi neko mogao da mi pomogne oko sledecih integrala:

x*arcsin[2x/(1+x²)]dx u granicama od 0 do √3 ;

dx/[1+e(exp(x/2))+e(exp(x/3))+e(exp(x/6))] ;

x*arctg[2x/(x²-1)]dx u granicama od 1 do 2 ;

?!?


(zao mi je sto ne znam kako da attach ujem slicice integrala nego mora da izgleda ovako nepregledno)! :)

Kod prvog i treceg radis parcijalnu i stavis da ti je u=x v="sve ostalo" i trebao bi da dobijes rezultat.