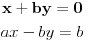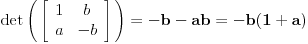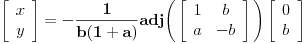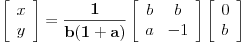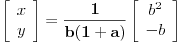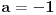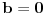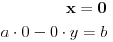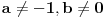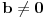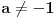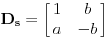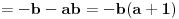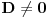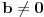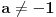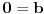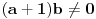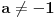[ BlaziX @ 11.01.2011. 18:59 ] @
| poštovani matematičari, spremam se za kolokvijum a ne kontam kojim algoritmom se rešavaju linearne jednačine kad je potrebno da ispitamo i šta treba da ubacimo da bi linearna jednačina bila odredjena neodredjena ili kontradiktorna. Da ne bih davio mnogo sa rečima okačiću par primera šta me konretno muči, bio bi vam zahvalan ako biste postupno rešili. 1. Oredi vrednosti parametara a,b koji pripada R za koju je sistem x+by=0 ax-by=b a)kontradiktoran b)odredjen c)1 puta neordedjen d)2 puta neoredjen 2. isti tekst ax+ay=b bx-by=a |