[ sannyy @ 15.01.2011. 22:15 ] @
| Trebam dokazati da je duzina bar jedne katete Pitagorinog trougla djeljiva s 3. Tek pocinjem uciti teoriju brojeva... pa mi treba pomoc, a vidim da ovdje ima ljudi koji to rasturaju. Unaprijed zahvaljujem! |
|
[ sannyy @ 15.01.2011. 22:15 ] @
[ Fermion @ 15.01.2011. 23:22 ] @
U principu, postavljač teme bi trebao da navede svoj postupak ideje i sl.
Ali ipak, odgovoriću. Dužine kateta iz Pitagorine trojke mogu se predstaviti na sledeći način: 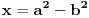  kao primitivna rešenja jednačine 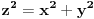 . .Pri tom su a i b prirodni brojevi različite parnosti, takvi da je 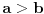 . Ako je bar jedan od brojeva a i b deljiv sa 3 tvrđenje je trivijalno tačno, y je deljivo sa 3. . Ako je bar jedan od brojeva a i b deljiv sa 3 tvrđenje je trivijalno tačno, y je deljivo sa 3.S obzirom da je 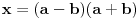 , jasno da pošto su a i b brojevi različite parnosti da su i , jasno da pošto su a i b brojevi različite parnosti da su i 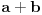 i i 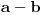 neparni brojevi. Pošto ni a ni b nije deljivo sa 3, bar jedan od brojeva a+b i a-b mora biti deljiv sa 3. neparni brojevi. Pošto ni a ni b nije deljivo sa 3, bar jedan od brojeva a+b i a-b mora biti deljiv sa 3.Prema tome, polazno tvrđenje je dokazano. [Ovu poruku je menjao Fermion dana 16.01.2011. u 02:03 GMT+1] [ petarm @ 15.01.2011. 23:26 ] @
[ Fermion @ 15.01.2011. 23:32 ] @
Nadam se da tema neće biti obrisana, pa ću posle, kad budem imao vremena, napisati i dokaz ovog tvrđenja sa Pitagorinim trojkama u vezi primitvinih rešenja.
Dodao bih samo još kako doći do toga da je ili a+b ili a-b deljivo sa 3, ako ni a ni b nije deljivo sa 3. Broj a je po modulu 3 kongruentan ili 1 ili -1. Broj b je po modulu 3 kongruentan ili 1 ili -1. U svim kombinacijama ovih ostataka njihov zbir ili razlika daje nulu u kongruenciji po modulu 3, pa je zaista i to tvrđenje ispunjeno. [ petarm @ 15.01.2011. 23:35 ] @
@ sanyy
Za ubuduce morao bi da naskrabas neki svoj postupak. Da se vidi da si krenuo da resavas i gde si zapeo. [ edisnp @ 15.01.2011. 23:42 ] @
Svaka trojka pozitivnih brojeva (a,b,c) koji pripadaju skupu celih brojeva
i koji zadovoljavaju jednacinu a^2+b^2=c^2 zove se trojka Pitagorinih brojeva i oni predstavljaju pravougli trougao.Najmanja trojka pitagorinih brojeva koji cine pravougli trougao je 3,4,5 uslov pitagorinih brojeva je da su uzajamno prosti tj.nemaju zajednickog delioca,i od ta tri broja se formiraju svi ostali brojevi tj trouglovi. Ako na primer jednacinu a^2+b^2=c^2 pomnozimo nekim celim brojem k>0 dobicemo novu trojku pitagorinih brojeva koji cine pravougli trugao kod kojih su bar dva medjusobno prosta (k*a)^2+(k*b)^2=(k*c)^2. Posto osnovnu trojku pitagorinih brojeva (3.4.5) mnozimo nekim brojem k>0 jasno je da bar jedna stranica tog pravouglog trougla mora biti deljiva sa 3 jer smo trojku prethodno mnozili nekim celim brojem k>0.Evo primer:ako pomnozimo osnovnu trojku pitagorinih brojeva sa 6 dobicemo 18^3+24^2=30^2. A iz ovog primera zakljucujemo da su sve stranice deljive sa tri.Dalje da bar jedna stranica pravouglog trougla mora biti deljiva sa ti jer u osnovi imamo broj koji je deljiv sa tri a to je broj tri. [ sannyy @ 15.01.2011. 23:55 ] @
Hvala ljudi. Ok, iduci put cu ja ovdje da prenesem svoja razmisljanja i pokusaje. Samo se bojim da ce biti previse komicno, jer na koncu ja nisam na vasoj razini. Hajd necu se podcjenjivati ali me treba pogurati.
[ petarm @ 16.01.2011. 00:03 ] @
[ Fermion @ 16.01.2011. 00:15 ] @
[ Fermion @ 16.01.2011. 01:08 ] @
Da se nadovežem na prvu poruku s obzirom da sam u rešenju koristio nešto što prethodno nisam dokazao, a to je opšti oblik osnovnih Pitagorinih trojki.
Dakle, treba izvesti opšti oblik osnovnih trojki, odnosno primitivnih rešenja jednačine 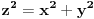 . Neka je to trojka . Neka je to trojka 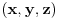 , pri čemu su ovi brojevi uzajamno prosti u parovima.Lako se pokazuje da su brojevi x i y različite parnosti, a z je pri tom naravno, neparno. Bez umanjenja opštosti predpostavimo da je x paran broj.Rešavanjem po , pri čemu su ovi brojevi uzajamno prosti u parovima.Lako se pokazuje da su brojevi x i y različite parnosti, a z je pri tom naravno, neparno. Bez umanjenja opštosti predpostavimo da je x paran broj.Rešavanjem po 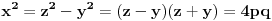 . Pošto je x parno možemo ga pisati u obliku . Pošto je x parno možemo ga pisati u obliku 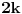 , pa je tada , pa je tada 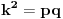 . S obzirom da je . S obzirom da je 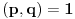 , pa su p i q kvadrati prirodnih brojeva. Neka je , pa su p i q kvadrati prirodnih brojeva. Neka je 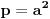 i i 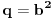 . Tada je . Tada je  , , 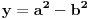 , , 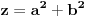 . Ovo naravno važi ako je . Ovo naravno važi ako je  , , 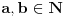 , a parnost a i b različita. Naravno i y mora biti veće od nule, tj. , a parnost a i b različita. Naravno i y mora biti veće od nule, tj. 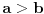 . .[ Nedeljko @ 16.01.2011. 10:08 ] @
Citat: petarm: Kvadrat prirodnog broja koji nije deljiv sa  pri deljenju sa pri deljenju sa  dace ostatak dace ostatak  . .  A ako ni  ni ni  nije deljivo sa nije deljivo sa  , onda bi , onda bi 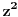 pri deljenju sa pri deljenju sa  dalo ostatak dalo ostatak  pa je pa je  ili ili  deljivo sa deljivo sa  . . Naravno  , ,  su katete, a su katete, a  je hipotenuza. je hipotenuza.Ovo je najjednostavnije tačno rešenje. [ Fermion @ 16.01.2011. 12:56 ] @
[ sannyy @ 16.01.2011. 20:58 ] @
@Fermion
E ja sam imala takvu ideju na pocetku. Ostatak pri djeljenju s 3 moze biti 0,1 i 2. 0 nisam uzimala u obzir jer je tad djeljivo s 3... pa sam isla dalje za 1 sam znala... tj ovo sto ste vi pokazali, stala sam kod 2 jer nisam raspisivala dokaz a nisam sebi mogla predociti to u glavi... medjutim sad i to znam... tj. (x==2(mod3))v(x==-2(mod3))=> x^2==4(mod3) (e ovdje nisam bila smanjila 4 po modulu 3 :( ...) ostalo isto... Na isti nacina sam dokazivala da ne postoji Pitagorin trougao kod kojih je duzina obje katete neparan broj. N-neparan, P-paran x^2+y^2=z^2 N^2+N^2=P^2 (1) Svaki paran broj kad se kvadrira dobije se broj koji je djeljiv s 4, tj (2k)^2==0(mod4) (2) (2k+1)^2==1(mod4) (3) Sada iz (1), (2) i (3) imamo: 1+1=0 (kontradikcija :) ) [ sannyy @ 23.01.2011. 20:50 ] @
Da li se formula
[d(m^2-n^2)]^2+[d(2mn)]^2=[d(m^2+n^2)]^2 koristi samo kada odredjujemo primitivne pitagorine trouglove, ili se moze koristiti i kod zadataka u kojem samo kaze da nadjemo sve pitagorine trouglove??? [ Nedeljko @ 23.01.2011. 23:29 ] @
Hajde razmisli. Šta su primitivne Pitagorine trojke, a šta one druge? Da li je skup brojeva ovog oblika zatvoren za množenje.
[ sannyy @ 24.01.2011. 10:13 ] @
(x,y,z) je primitivna trojka ako su x,y i z relativno prosti. Primitivni pitagorin trougao je onaj kod kojeg su stranice primitivna trojka.
Npr. pitagorin trougao cije su stranice (3,5,7) je primitivn, a pitagorin trougao cije su stranice (6,8,10) nije primitivan. Eh sad zatvorenost skupa u odnosu na mnozenje... govorimo o skupu N, a on je zatvoren u odnosu na mnozenje. Da mi je ovakvo moje razmisljanje pomoglo, pa i nije. Kroz zadatke sam skontala da tu formulu upotrebljavam bez obzira na ono "primitivni". Da me ko pita zasto... rekla bih da ne znam.:( [ Nedeljko @ 24.01.2011. 10:41 ] @
[ sannyy @ 24.01.2011. 12:41 ] @
Hvala najljepsa! Puno ste mi pomogli oko ovih trojki.
Jos nesto... htjela bih malo raditi teoriju brojeva, ali bas nemam literature... pa ako znate kakvu dobru knjigu, zbirku... ili neki link... :$... Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|