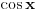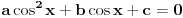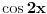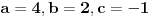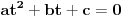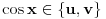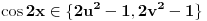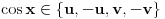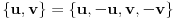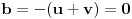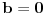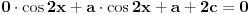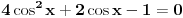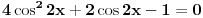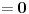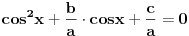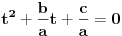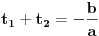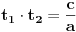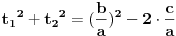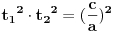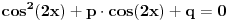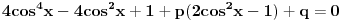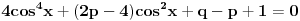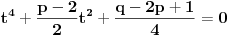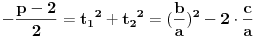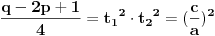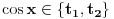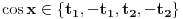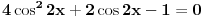[ Nedeljko @ 17.01.2011. 12:49 ] @
|
[ petarm @ 17.01.2011. 13:19 ] @
[ Sini82 @ 17.01.2011. 15:07 ] @
[ Nedeljko @ 17.01.2011. 15:51 ] @
[ Nedeljko @ 17.01.2011. 15:54 ] @
[ Fermion @ 17.01.2011. 22:30 ] @
Potpuno se slažem sa Nedeljkovim rešenjem. S tim što bi možda trebalo ispitati i slučajeve kada t nije u intervalu (-1,1), ali to se svodi na isto, ispada da je b=0. Ipak to ne mora da znači da je drugi deo zadatka pogrešan što se uzima b=-1, prosto sledi da slučaj nemoguć, mislim da je funkcija tog dela zadatka da pomalo zbuni rešavača.
[ Sini82 @ 18.01.2011. 08:41 ] @
Formirana jednačina mora da ima ista rješenja kao polazna, što ne znači da mora da ima isti skup rješenja. Nigdje u tekstu zadatka nije rečeno da jednačine moraju biti ekvivalentne.
Tako sam ja shvatio. Nedeljko je u pravu ako tražimo da polazna i formirana jednačina imaju iste skupove rješenja. [ Nedeljko @ 18.01.2011. 08:55 ] @
A u čemu je razlika između "imati ista rešenja" i "imati iste skupove rešenja"? Koliko se ja razumem u matematiku, to je isto.
[ Sini82 @ 18.01.2011. 11:23 ] @
[ Sini82 @ 18.01.2011. 12:19 ] @
Našao sam zadatke i rješenja u "The IMO Compendium" naših autora (Dušan Đukic, Vladimir Janković, Ivan Matić, Nikola Petrović).
Rješenja su ista kao ona koja sam ja dobio, provjerio sam; 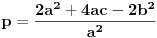 i i 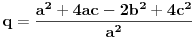 ; ;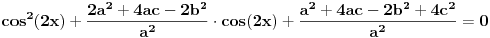 . .Bojan Bašić: uklonjen link ka piratskom sadržaju. [Ovu poruku je menjao Bojan Basic dana 18.01.2011. u 14:42 GMT+1] [ Fermion @ 18.01.2011. 13:13 ] @
Citat: Nedeljko: A u čemu je razlika između "imati ista rešenja" i "imati iste skupove rešenja"? Koliko se ja razumem u matematiku, to je isto. Ukoliko bi zadatak bio ovo drugo, tj. da se traži da skupovi rešenja budu isti, pitam se da li bi se u rešenje računalo da ako su oba skupa prazna, tj. da obe jednačine nemaju rešenje, da su im skupovi rešenja ekvivalentni? [ Nedeljko @ 18.01.2011. 13:31 ] @
Citat: Sini82: E pa vidiš, jednačina 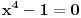 ima ista ona rješenja koja ima i jednačina ima ista ona rješenja koja ima i jednačina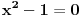 , ali te dve jednačine nemaju iste skupove rješenja. , ali te dve jednačine nemaju iste skupove rješenja.Pa, skup rešenja je u oba slučaja 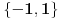 ili ako ti se više sviđa ili ako ti se više sviđa 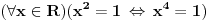 . .Citat: Fermion: Ukoliko bi zadatak bio ovo drugo, tj. da se traži da skupovi rešenja budu isti, pitam se da li bi se u rešenje računalo da ako su oba skupa prazna, tj. da obe jednačine nemaju rešenje, da su im skupovi rešenja ekvivalentni? Da, ekvivalentne znači da je nešto rešenje jedne akko je rešenje i druge, tj. da imaju isti skup rešenja. [ Nedeljko @ 18.01.2011. 13:32 ] @
Citat: Sini82: Našao sam zadatke i rješenja u "The IMO Compendium" naših autora (Dušan Đukic, Vladimir Janković, Ivan Matić, Nikola Petrović). Rješenja su ista kao ona koja sam ja dobio, provjerio sam; 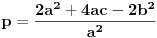 i i 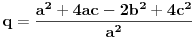 ; ;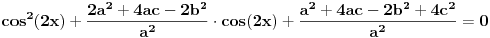 . .Još samo da su dobra, tj. da su rešenja. [ Sini82 @ 18.01.2011. 13:47 ] @
^
Netačno. Skup rješenja jedne jednačine je {1, -1} a druge {1, -1, i, -i}, tako da te dvije jednačine nisu ekvivalentne. ^ Nisi dobro preveo originalan tekst ili ga ne tumačiš kako treba ili smo svi mi u krivu a ti si u pravu. Ako jesi u pravu, ovo nije zadatak sa prve međunarodne matematičke olimpijade nego sa neke pismene školske zadaće. [ Nedeljko @ 18.01.2011. 14:23 ] @
Mislio sam da tražiš realna rešenja. Ne znam kako drugačije da protumačim ovo
Citat: Što se prevoda tiče, okačio sam engleski original u prilogu prve poruke. Ako se tražilo da svako rešenje polazne jednačine bude rešenje formirane jednačine, ali ne i obrnuto, onda je 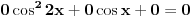 trivijalno rešenje. Doduše, ona nije kvadratna, ali ni u rešenju koje si postavio ne mora biti trivijalno rešenje. Doduše, ona nije kvadratna, ali ni u rešenju koje si postavio ne mora biti 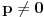 . .[ Fermion @ 18.01.2011. 14:50 ] @
Slažem se da postoji nejasnoća, tj. nije precizirano šta znači da jednačine imaju dva ista rešenja.
1)Rešenja prve jednačine su ujedno rešenja druge (skup rešenja druge jednačine sadrži skup rešenja prve) 2)Sva rešenja prve jednačine su rešenja druge jednačine i sva rešenja druge su rešenja prve (skupovi rešenja obe jednačine su jednaki (ekvivalentni)). Slučajevi 1 i 2 su različiti, pa su i rešenja različita, pa je to stvar interpretacije. Zavisno od tumačenja zadatka imamo razna rešenja. Intuitivno, bliži sam drugom tumačenju, s tim što nigde nisam nailazio na preciznu definiciju toga šta znači to da su rešenja dve jednačine ista. Citat: Nedeljko: Da, ekvivalentne znači da je nešto rešenje jedne akko je rešenje i druge, tj. da imaju isti skup rešenja. Ja sam pitao za nešto drugo. U slučaju da obe jednačine nemaju (realnih) rešenja skup rešenja za obe je prazan skup. To dalje znači da su im skupovi rešenja ekvivalentni. Vaše rešenje ne razmatra tu mogućnost. [ Nedeljko @ 18.01.2011. 14:53 ] @
[ Nedeljko @ 18.01.2011. 15:18 ] @
Citat: Fermion: Slažem se da postoji nejasnoća, tj. nije precizirano šta znači da jednačine imaju dva ista rešenja. 1)Rešenja prve jednačine su ujedno rešenja druge (skup rešenja druge jednačine sadrži skup rešenja prve) 2)Sva rešenja prve jednačine su rešenja druge jednačine i sva rešenja druge su rešenja prve (skupovi rešenja obe jednačine su jednaki (ekvivalentni)). Ne znam šts si hteo da kažeš sa onim "dva" koje sam zacrnio u citatu, ali zna se šta znači da jednačine imaju ista rešenja. To je ovo pod 2). Ovo pod 1) bi se izrazilo rečima "iz prve jednačine sledi druga". [ Fermion @ 18.01.2011. 15:24 ] @
Nije dva nego sva, štamparska greka, d je pored s na tastaturi, a kucao sam na brzinu
[ IdeaR @ 18.01.2011. 20:58 ] @
Citat: Nedeljko: Da, jednačine 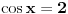 i i 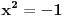 nad skupom realnih brojeva kao domenom su ekvivalentne. Taj slučaj nisam razmatrao, a poenta je da zadatak nije dobro postavljen. nad skupom realnih brojeva kao domenom su ekvivalentne. Taj slučaj nisam razmatrao, a poenta je da zadatak nije dobro postavljen.Rezon ti je sasvim korektan, zadatak nije dobro (precizno) formulisan. Čestitam na pažljivom rješavanju i dobrom zapažanju, većina jednostavno preleti preko ovakvih pojedinosti. [ Sini82 @ 19.01.2011. 08:11 ] @
Citat: Originalni tekst zadatka (eng.pdf): 1959/3. Let a, b, c be real numbers. Consider the quadratic equation in cos x : a 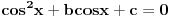 . .Using the numbers a, b, c, form a quadratic equation in cos 2x, whose roots are the same as those of the original equation. Compare the equations in cos x and cos 2x for a = 4, b = 2, c = −1. Citat: Ne može koeficijent uz kvadratni član biti nula (jer onda ne bi bile kvadratne jednačine), ni u jednoj ni u drugoj jednačini, tako da to trivijalno rješenje otpada; što je zadovoljeno u prvoj jednačini 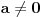 i u drugoj jer je koeficijent uz kvadratni član i u drugoj jer je koeficijent uz kvadratni član  . .Ne mora da bude. Npr. za 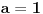 , , 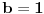 , , 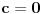 imamo imamo 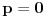 ; p je koeficijent uz linearni član. ; p je koeficijent uz linearni član.Recimo, kažem nekome:"Imam iste te knjige koje ti imaš." To ne znači da imam samo te knjige i nikoje druge. Recimo, da i taj neko meni kaže:"Imam i ja iste te knjige koje ti imaš." Tada imamo iste knjige (ili ih obojica uopšte nemamo; u tom slučaju smo se našalili). Analogna je stvar sa našim jednačinama i rješenjima, kao sa nama dvojicom i knjigama. Za mene, nema sumnje, kako treba tumačiti tekst zadatka. I u engleskom jeziku postoji pojam equivalent equation. Citat: http://wiki.answers.com/Q/What_is_equivalent_equation Two equations are said to be equivalent if and only if they have the same solutions. Vjerovatno bi bio i u originalnom tekstu zadatka, da je to ono što treba da se traži. [Ovu poruku je menjao Sini82 dana 19.01.2011. u 13:43 GMT+1] [ Nedeljko @ 19.01.2011. 11:17 ] @
Pa, po citatu koji si naveo "imati ista rešenja" i "biti ekvivalentni" znači isto.
[ Sini82 @ 19.01.2011. 12:41 ] @
Obrati pažnju na "ako i samo ako imaju ista rješenja".
[ Nedeljko @ 19.01.2011. 14:17 ] @
Pa, da, to znači da je to dvoje isto.
[ Sini82 @ 19.01.2011. 18:45 ] @
U tekstu zadatka ne piše da "imaju ista rješenja", nego da druga jednačina ima rješenja koja ima prva jednačina, ne da važi i obratno.
[ Nedeljko @ 19.01.2011. 20:32 ] @
Engleska reč "same" znači "isto".
Da su tako formulisali zadatak kako si ga ti sada formulisao, bilo bi u redu. Tačan prevod od "Using the numbers a, b, c, form a quadratic equation in cos 2x, whose roots are the same as those of the original equation." je "Koristeći brojeve a, b, c, sačiniti kvadratnu jednačinu po cos 2x čiji su koreni isti kao oni od polazne jednačine." [ Sini82 @ 19.01.2011. 21:50 ] @
Iskreno, loš sam skroz sa engleskim. Vjerujem da si ti mnogo bolji. Ne mogu vjerovati da su pogrešno formulisali zadatak na takmičenju takvog ranga. Još prva olimpijada. Mislio sam, možda postoje neke konvencije među matematičarima što se tiče engleskog jezika, pa da se tako neke stvari podrazumijevaju. Stvarno, ne znam. Nisam nikad bio ni blizu takmičenjima toga nivoa, pa i ne znam kako to zapravo ide. I sam sam na neke načine učestvovao u takmičenjima, dešava se ne samo da pogriješe tekst zadatka, nego i rješenje. Što je onda najgore, desi se da niko iz komisije koja pregleda zadatke ne zna da ga uradi. Tako da je sve moguće. Čudi me da su toliki ljudi te zadatke od 1959. do danas prepisivali, iščitavali, rješavali a da nisu ispravili grešku.
[ kandorus @ 19.01.2011. 22:30 ] @
Tačan prevod od "Using the numbers a, b, c, form a quadratic equation in cos 2x, whose roots are the same as those of the original equation."
je "koristeći brojeve a, b, c, formirati neku kvadratnu jednačinu u cos 2x, čiji koreni su isti kao oni od originalne jednačine." Postavlja se pitanje koji je smisao "in cos 2x". Bukvalno to je "u cos 2x". Ali ako se pogleda prethodni pasus "Consider the quadratic equation in cos x" zaključak je da je pravilan prevod (u skladu sa onim kako se mi izražavamo) "po cos 2x". Dakle "koristeći brojeve a, b, c, formirati neku kvadratnu jednačinu po cos 2x, čiji koreni su isti kao oni od originalne jednačine." [ Nedeljko @ 19.01.2011. 23:14 ] @
"Solve in x" znači "reši po x", tj. nađi za koje x to važi.
Kvadratna jednačina po t je jednačina oblika at2+bt+c=0, gde su a, b i c konstante od kojih je a različita od nule. Tu t može biti i funkcija. [ kandorus @ 19.01.2011. 23:47 ] @
Pa u tome je cela poenta. Obe jednačine se svode na rešavanje jednačine po t u ekvaivalentnoj jednačini pa su im (skupovi) rešenja "po cosx" i "po cos2x" jednaka. Naravno, "po x" se rešenja razlikuju ali to se i ne traži. U drugom delu zadatka se za date parametre a, b, c, daje očit primer koji služi da uputi rešavača.
Hoću da kažem da ne treba tražiti neku "previsoku" matematiku u ovom zadatku, barem ne u nameni koja mu je odredjena (pretpostavljam srednješkolska olimpijada). Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|