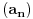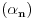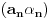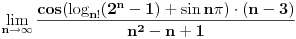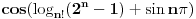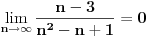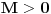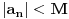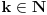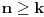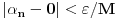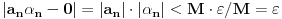[ Fermion @ 20.01.2011. 17:52 ] @
|
| Evo jednog interesantnog zadatka.
(Časopis "Tangenta" broj 59, str.42, "Granična vrednost niza", zadatak broj 2)
a)Ako je 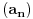 ograničen, a ograničen, a 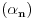 nula niz, dokazati da je nula niz, dokazati da je 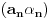 nula niz. nula niz.
b)Naći 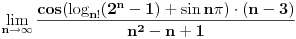
Ja sam se trudio da ovaj zadatak rešim, ali nisam ostvario nikakav značajan pomak pod a), pod b) mislim da sam rešio. Pod a) mi je intuitivno jasno zašto važi tvrđenje, ali ne mogu da smislim strog matematički dokaz.
Ovo pod b) bi, onda verovatno bila posledoca tvrđenja pod a). Tj. zbog ovog kosinusa niz 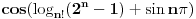 je ograničen, a pošto trivijalno važi: je ograničen, a pošto trivijalno važi:
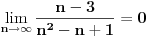 sledi da je ovo nula niz pa bi onda rešenje trebalo da bude nula jer je to ovde upravo odgovarajuća granična vrednost nula niza. sledi da je ovo nula niz pa bi onda rešenje trebalo da bude nula jer je to ovde upravo odgovarajuća granična vrednost nula niza. |
[ Nedeljko @ 20.01.2011. 18:54 ] @
Mora da se šališ.
Prvo, postoji konstanta
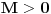
takva da za svako

važi
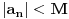
.
Neka je dato

. Izaberimo takvo
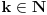
da za sve

takve da je
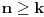
važi
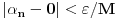
. Za tako izabrano

je za sve

takve da je
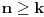
ispunjeno
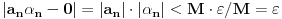
.
[ Fermion @ 21.01.2011. 09:57 ] @
Ne baš. Mada je zaista elementarno. Malo mi nedostaje teorijskih znanja iz ove oblasti, otuda sam dokazivao nešto sasvim drugo i to nisam mogao da dokažem jer je pogrešno

. Hvala.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.