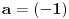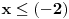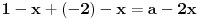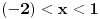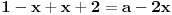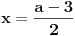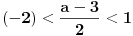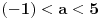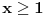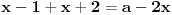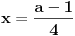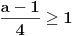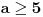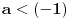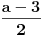[ Akycy @ 27.01.2011. 22:34 ] @
| Trebam resiti jednacinu: Skup vrednosti realnog parametra a za koje jednacina |x-1|+|x+2|=a-2x ima maksimalan broj razlicitih realnih resenja je oblika?Resenje je: 1.|x-1|=x-1,za x-1>0 , |x+2|=x+2,za x+2>0 zajadnicki uslov je x>1 x>1 x>-2 i sad kad sredimo datu jednacinu dobicemo a=4x+1 vrednost x nam je od 1 pa do beskonacno 2.|x-1|=-x+1,za x-1<0 |x+2|=-x-2,za x+2<0 zajednicki uslov je x<-2 x<1 x<-2 sredjivanjem jednacine dobicemo da je a=-1 3.|x-1|=x-1,za x-1>0 |x+2|=-x-2,za x+2<0 u ovom slucaju jednacina nema resenja. x>1 x<-2 4.|x-1|=-x+1,za x-1<0 |x+2|=x+2,za x+2>0 tj.x=(-2,1) x<1 x>-2 sredjivanjem jednacine dobicemo a=3+2x. Zbunjujeme ovo da se odredi skup vrednosti realnog parametra a za koje jednacina ima maksimalan broj razlicitih realnih resenja tacnije ne znam sta to znaci i interesuje me da li sam ovo gore dobro odradila jer ne znam posto nemam resenja zadatka. |