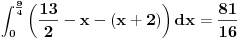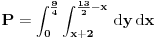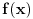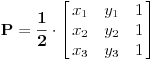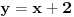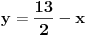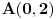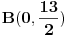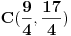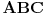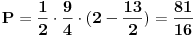[ edisnp @ 29.01.2011. 17:11 ] @
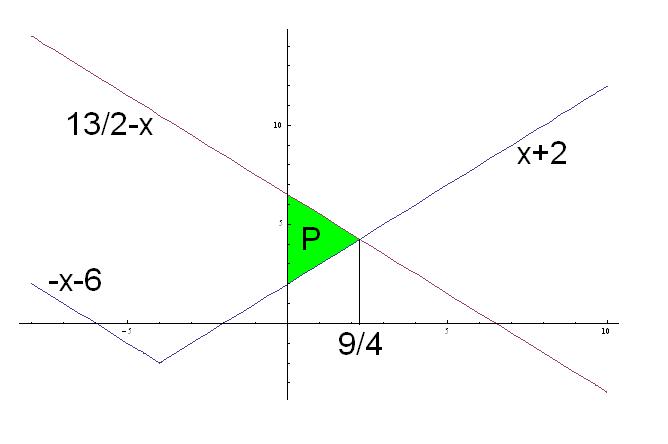
| Imam problema oko resenja jednog zadatka treba da izracunam povrsinu torugla koju je ogranicen ordinatom i pravama y=|x+4|-2 i 2x+2y-13=0. Kad odredima pravu 2x+2y-13=0 prvo nadjem vrednosti za x i za y i posle kad odredjujem pravu y=|x+4|-2 uzmem vrednost za x>0 dobijamo y=x+2 , a za x<0 dobijam y=-x-6 i nikako mi ne ispada dobro i zbunjuje me imamo ovu apsolutnu vrednost i valjda zbog toga dobijamo dve prave od koje jedna odredjuje trougao a druga ne odredjuje sve u svemu ne ide mi da odredim povrsinu ovog trougla. |