|
|
[ sannyy @ 01.02.2011. 13:12 ] @
|
|
Eulerova funkcija je multiplikativna, tj. ako su m i n relativno prosti, onda vrijedi fi(m*n)=fi(m)*fi(n).
Moze li ni neko pomoci oko dokaza ove teoreme? |
[ Nedeljko @ 01.02.2011. 14:21 ] @
Za 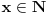 neka je 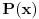 skup svih prirodnih brojeva ne većih od  , koji su uzajamno prosti sa  i neka je 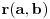 ostatak pri delenju prirodnog broja  prirodnim brojem  . Sa 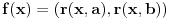 definisana je jedna bijekcija skupa 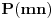 u skup 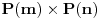 . Pokušaj to da dokažeš.
Ako su  i  uzajamno prosti, onda je  uzajamno prosto sa  akko je uzajamno prosto kako sa  , tako i sa  . Odatle sledi dobra definisanost funkcije  .
Odatle i iz kineske teoreme o ostacima sledi da je ta funkcija surjektivna.
Ako je 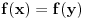 , onda je 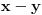 deljivo kako sa  , tako i sa  . Stoga je deljivo i sa 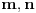 , što je na datom domkenu moguće samo za 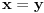 . Odatle sledi injektivnost.
To ti je skica, pa je upotpuni. [ sannyy @ 01.02.2011. 21:38 ] @
Hvala... pokusacu sad da se malo zabavim ovim...
A evo dokaza koji meni i nije bas legao... ide ovako...
Neka je nzd(m,n)=1 i neka a i b prolaze reduciranim sistemom ostataka modulo m, odnosno modulo n.
Eh cilj je pokazati da an+bm prolazi reduciranim sistemom ostataka modulo mn... i ako se to pokaze dobije se da je fi(mn)=fi(m)*fi(n) ( a meni nije jasno kako se to dobije)
Dalje...
Kako je nzd(a,m)=1 i ndz(b,m)=1, to je broj an+bm relativno prost s m i s n (nejasno)
Svaka dva broja takvog oblika su nekongruentni modulo mn.
Iz an+bm==a'n+b'm(mod mn) slijedi (a-a')n==(b'-b)m (mod mn), odavde m|a-a' i n|b'-b, pa je a=a' i b=b'.
Treba pokazati jos da ako je nzd(c,mn)=1 da je c==an+bm (mod mn) za neke a i b.
Kako je ndz(m,n)=1 to postoje cijeli brojevi x i y takvi da je mx+ny=1.
Ocito je nzd(cy,m)=1 i nzd(cx,n)=1, pa brojevi a i b definirani s cy==a (modm) i cx==b (modn) imaju trazena svojstva.
[ sannyy @ 01.02.2011. 22:59 ] @
Evo jos jedne teoremice...
Neka su a i m prirodni brojevi, te b cijeli broj. Kongruencija ax==b (mod m) ima rjesenje akko d= nzd(a,m) dijeli b.
Ako je ovaj uvijet zadovoljen, onda gornja kongruencija ima tacno d rjesenja modulo m.
Dokaz:
Ako kongruencija ax==b (mod m) ima rjesenje onda postoji y iz skupa cijelih broojeva tako da je ax-my=b.
Tada imamo da nzd(a,m) dijeli b. Pretpostavimo da d=nzd(a,m) dijeli b. Stavimo da je a'=a/d, b'=b/d i m'=m/d. ( zasto uzimamo ovo a' i b'?)
Sada trebamo rijesiti kongruenciju a'x==b' (modm'). Nzd(a',m')=1, pa x prolazi potpunim sistemom, tj. svaki ostatak mod m' (pa tako i b')se dobija tacno za jedan x iz potpunog sistema ostataka mod m'.
Ako je x' rjesenje kongruencije a'x'==b' (mod m'), onda su sva rjesenja od ax==b (mod m) u cijelim brojevima dana s x=x'+nm', n je prirodan broj,
a sva neekvivalentna rjesenja dana su s x=x'+nm', n=0,1,2,3, ... ,d-1.
Dakle, ako d dijeli b, onda kongruencija ax==b (mod m) ima tacno d rjesenja mod m
[ Nedeljko @ 02.02.2011. 09:23 ] @
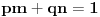 za neke 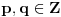 . Pritom je  uzajamno prosto sa  , a  uzajamno prosto sa  . Neka je  uzajamno prosto sa  . To tačno znači da je  uzajamno prosto sa  i  . No, tada je 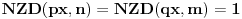 , kao i 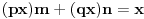 . Ako je 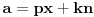 i 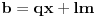 , onda je 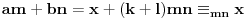 . Može se na primer uzeti da je  ostatak pri delenju 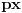 sa  , a  ostatak pri delenju 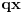 sa  . [ sannyy @ 05.02.2011. 11:22 ] @
Osnovna teorema aritmetike
Faktorizacija svakog prirodnog broja n>1 na proste faktore je jedinstvena, do na poredat prostih faktora.
Dokaz:
Pretpostavimo suprotno, tj. da postoje dvije razlicite faktorizacije broja n.
Dijeljeci te dvije faktorizacije s prostim brojevima koji su zajednicki objema reprezentacijama, dobicemo jednakost oblika:
p1*p2*...*pk=q1*q2*...*ql
gdje su pi i qi prosti brojevi, ne nuzno razliciti, ali takav da se nijedan prost broj s lijeve strane ne pojavljuje na desnoj.
Medjutim, jer iz p1|q1*q2*...*ql (nije mi jasno otkud ovo), slijedi da p1 dijeli barem jedan qi, a to je kontradikacija.
[ Nedeljko @ 05.02.2011. 18:17 ] @
Neka je 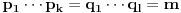 .
Iz 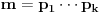 sledi da 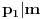 , a odatle i iz 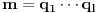 da 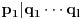 . No, obzirom da je 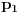 prost broj, odatle sledi da 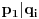 za neko 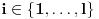 . [ sannyy @ 05.02.2011. 18:26 ] @
Razumjela. :)
Hvala!
[ nikmil @ 06.02.2011. 15:20 ] @
Evo još jednog dokaza multiplikativnosti Ojlerove funkcije.
Broj automorfizama ciklične grupe 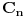 jednak je upravo 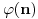 : 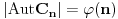 .
Lako se dokazuje da za uzajamno proste  i  važi 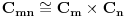 , pa je 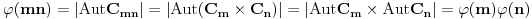 .
[ sannyy @ 10.02.2011. 16:30 ] @
Moze li mi neko pomoci oko dokaza Wilson-ove teoreme...
Ako je p prost broj, onda je (p-1)!==-1 (mod p). ?
[ sannyy @ 14.02.2011. 17:09 ] @
Dokaz Wilson-ove teoreme:
Za p = 2 i p = 3 kongruencija je ocito zadovoljena.
Pretpostaviti da je p>=5. Grupirajmo clanove skupa {2,3,..., p-2} u
parove (i,j) sa svojstvom i * j ==1 (mod p).
Ocito je i razlicito od j jer bi inace broj (i - 1)(i + 1) bio djeljiv sa p,
a to je nemoguce zbog 0 < i ¡ 1 <i + 1 < p.
Tako dobivamo p-3/2 parova i ako pomnozimo odgovarajucih p-3/2
kongruencija, dobicemo
2 * 3 *...* (p - 2) == 1 (mod p);
pa je
(p -1)!== 1(mod p).
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|