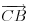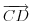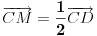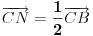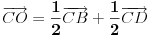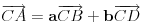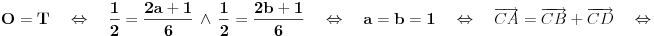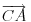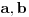[ Akycy @ 01.02.2011. 19:39 ] @
|
| Ozbiljno sam se namucila oko jednog zadatka i zaista nikako mi ne
uspeva da ga resim odlucila sam da ga postavim na ovom forumu ako neko
ima neku ideju ili resenje neka ga izlozi.Unapred zahvalna.
U konveksnom cetvorouglu ABCD tacka M je srediste stranice CD a tacka
N srediste stranice BC.Presek dijagonala O cetvorougla ABCD je teziste trougla AMN ako i samo
ako je cetvorougao ABCD paralelogram.DOKAZATI. |
[ edisnp @ 01.02.2011. 20:40 ] @
Mozda bi trebalo da se dokaze suprotno i onda se naidje na neku
kontradiktorsnost iz koje sledi da je to moguce samo ako je cetvorougao
paralelogram.
[ Nedeljko @ 02.02.2011. 09:28 ] @
Ovo se lako rešava vektorskom algebrom. Izrazi sve preko vektora
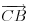
i
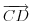
.
[ Akycy @ 02.02.2011. 18:33 ] @
Opet nemogu da dobijem resenje ako bi neko mogao da
mi opsirnije objasni ili da resenje.
[ Nedeljko @ 02.02.2011. 21:03 ] @
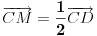
,
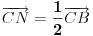
,
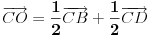
,
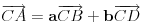
,

,
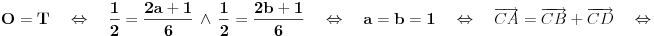
četvorougao
je paralelogram.
[ Akycy @ 03.02.2011. 19:13 ] @
Ovo mi nije jasno i nikako nemogu da ga dogijem
--> --> -->
CA=aCB+bCD nije mi jasno sta znace ovi koeficienti a i b
[ Nedeljko @ 03.02.2011. 20:49 ] @
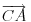
i
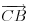
su linearno nezavisni vektori u ravni. Obzirom da ih je dva i da se radi o ravni, obrazuju bazu. Stoga se svaki vektor može prikazati kao njihova linearna kombinacija na tačno jedan način.
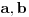
su neodređeni koeficijenti.
[ berazorica @ 04.02.2011. 01:21 ] @
Za slučaj da ne voliš vektore:
1. Ako je ABCD paralelogram, onda je presek dijagonala O težište tougla AMN:
Znajući da je MN srednja linija trougla BCD i kao takva paralelna i podudarna polovini BD, i da se dijagonale paralelograma polove, ako sa S označimo presek MN i AC, lako se zaključuje da MS=SN i AO:OS =2:1, što znači da je O težište trougla AMN.
2. Ako je O težište trougla AMN, onda je ABCD paralelogram:
Kako je AS težišna linija, znamo da je MS=SN. Iz sličnosti trouglova očigledno BO=OD.
Kako je MN srednja linija trougla BCD, sledi OS=SC, a kako je O težište, znamo da je AO=2 OS, pa odatle AO=OC.
Dakle, dijagonale ovog konveksnog četvorougla se polove, pa je on paralelogram.
[ edisnp @ 04.02.2011. 21:16 ] @
Na isti nacin kao berazorica sam i ja uradio zadatak ali posto ti je vec
Nedeljko poslao extra resenje mislio sam da je suvisno mozda je kod
vektorske metode malo teze naci vektor CO sve ostalo je lako.
[ Akycy @ 16.02.2011. 14:11 ] @
kako ste ovo dobili 1/2=2a+1/6
i 1/2=2b+1/6
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.