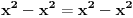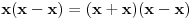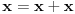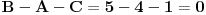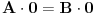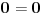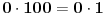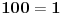[ Horvat @ 07.02.2011. 10:43 ] @
|
| nisam znao kako drugacije da srocim naslov
problematika je sledeca (izvor):
A=4
B=5
C=1
C = B-A |*(B-A)
C(B-A) = (B-A)2
CB-CA = B2-2AB+A2 |-A2
CB-A2-CA = B2-2AB |+AB
AB+CB-A2-CA = B2-AB |-CB
AB-A2-CA = B2-AB-CB
A(B-A-C) = B(B-A-C)
do ove tacke je jednakost tacna, medutim kada se skrate (B-A-C) s obe strane, dobije se
A(B-A-C) = B(B-A-C) | /(B-A-C)
A = B
4 = 5
sto nije tacno
sta je u ovom resanju netacno? meni nije nista zapalo za oko |
[ japan @ 07.02.2011. 10:51 ] @
Iz A*0 = B*0 ne sledi A = B
[ djoka_l @ 07.02.2011. 11:06 ] @
B-A-C = 0
Ne može da se skrati jer je izraz kao što je pre mene napisao japan
[ Nedeljko @ 07.02.2011. 11:10 ] @
Evo poznatije i jednostavnije demonstracije iste greške:
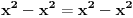 ,
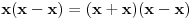 ,
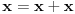 . [ X Files @ 07.02.2011. 11:15 ] @
^
Upravo taj primer su nam još u osnovnoj školi naveli kao "zanimljivost", a uz to naravno i obrazloženje.
[ Fermion @ 07.02.2011. 12:06 ] @
Citat: Horvat
do ove tacke je jednakost tacna, medutim kada se skrate (B-A-C) s obe strane, dobije se
A(B-A-C) = B(B-A-C) | /(B-A-C)
A = B
4 = 5
sto nije tacno
sta je u ovom resanju netacno? 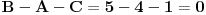
Prema tome 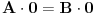 i 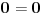 . Dakle nula se ne sme kratiti.
Može da se napiše i 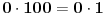 , pa bi se onda dobilo 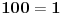 .
Malo se ponavljam u odnosu na prethodne poruke, ali dobro. Ima još dosta takvih dokaza ali oni nemaju mnogo smisla, bar po meni, osim što su dobra ilustracija nekih pravila sa uslovima koji moraju biti ispunjeni, a na koje se nekad ne obraća pažnja. [ zzzz @ 07.02.2011. 14:09 ] @
Osim sa nulom zabranjeno je dijeliti sa (1+NE),gdje je NE različito od -1.
Evo dokaza:
UČITI=NE LJENČARITI
NE UČITI=LJENČARITI
--------------------------
zbrojimo jednačine:
UČITI+NE UČITI=NE LJENČARITI+LJENČARITI
UČITI(1+NE)=LJENČARITI(1+NE)
--------------------------
ako skratimo sa (1+NE) dobijemo kontradikciju:
UČITI=LJENČARITI
Ubuduće nikad ne kratite sa (1+NE)!
[ Horvat @ 07.02.2011. 14:44 ] @
Citat: japan: Iz A*0 = B*0 ne sledi A = B
jeste to, ali ti ne moras uvrstiti zamenu onda, ti onda gledas samo promenljive A B i C, njihova vrednost nije bitna, s obe strane je isto u zagradama, pa po mozes skratiti to
ili moras prilikom svakog skracivanja proveriti da li je nula ili 1+ne?
evo i nedeljko je dao jedan primer
kako matematika tretira te probleme? [ djoka_l @ 07.02.2011. 14:53 ] @
Citat: ili moras prilikom svakog skracivanja proveriti da li je nula ili 1+ne?
Upravo ovako. Kada god skraćuješ neki izraz moraš da uvedeš pretpostavku da ga skraćuješ sa nečim različitim od nule.
Na primer, ako deliš sa 1+x, onda kažeš da je izraz koji deliš jednak onom koji dobiješ kao rezultat za svako x različito od -1 [ Horvat @ 07.02.2011. 15:07 ] @
ajd ovako, ne znamo koje su vrednosti a b i c [edit] nek A bude nepoznato,tj A se trazi[/edit]
imamo
A(B-A-C) = B(B-A-C)
A(B-A-C) - B(B-A-C) = 0
(B-A-C)(A-B) = 0
iz ovoga sledi da je ili
(B-A-C) = 0
ili
A-B=0
za 1. slucaj je A = B-C (sto i jeste tacno)
a za 2. A=B (sto nikako nije tacno)
[edit] po ovome se dobije da je A=4 ili A=5, kako znas koje je tacno?[/edit]
sta cemo tu?
[ mulaz @ 07.02.2011. 15:12 ] @
Kad iz ovoga:
(B-A-C)(A-B) = 0
prelazis na:
(B-A-C) = 0
u stvari dels jednacinu sa (A-B), i dobijas:
(B-A-C) = 0/(A-B)
Ako je (A-B) jednako 0, dobijas nedifinisan izraz.
Isto vazi za drugi primer
A u svakom slucaju, ako delis nesto sa necim (recimo 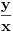 ), to smes da uradis tek kada znas da x NIJE jednak 0, ili napomenuti da jednacina ne vazi u toj tacki.
[ Horvat @ 07.02.2011. 15:13 ] @
ok, ne mozes deliti, mozes prebaciti na drugu stranu i oduzeti, pogledaj post iznad
edit:
da, to sam zaboravio :D
[ mulaz @ 07.02.2011. 15:21 ] @
Citat: Horvat:
(B-A-C)(A-B) = 0
iz ovoga sledi da je ili
(B-A-C) = 0
ili
A-B=0
Kako si dosao do ove dve jednacine, bez da si originalnu podelio sa ostatkom onda? [ Fermion @ 07.02.2011. 15:24 ] @
Citat: Horvat:
za 1. slucaj je A = B-C (sto i jeste tacno)
a za 2. A=B (sto nikako nije tacno)
Da bi proizvod ta dva člana bio 0 potrebno je i dovoljno da bar jedan od njih bude jednak nuli. Dakle radi se o tome da je ili jedno ili drugo, ali ne i obavezno i jedno i drugo jednako nuli. [ Horvat @ 07.02.2011. 15:25 ] @
skontah u medjuvremenu
stao mi bio mozak
[ atelago @ 08.02.2011. 00:04 ] @
1 C = B-A |*(B-A)
2 C(B-A) = (B-A)2
3 CB-CA = B2-2AB+A2 |-A2
4 CB-A2-CA = B2-2AB |+AB
5 AB+CB-A2-CA = B2-AB |-CB
6 AB-A2-CA = B2-AB-CB
7 A(B-A-C) = B(B-A-C)
Mislim da je greška napravljena u petom redu, jer su, oduzimanjem
vrednosti CB, obe strane jednačine namerno svedene na nulu, odnosno
šesti red bi konkretno bio ovakav:
4 · 5 – 4 · 4 – 1· 4 = 5 · 5 – 4 · 5 – 1 · 5
i leva i desna strana su nule t. j. 0 = 0, a umesto toga računica
se nastavlja rastavljajući formalno te nule na činioce u sedmom redu
ovako: A · (B-A-C) = B · (B-A-C), ali računica je već gotova, a nastavak
je posledica primene formalizma u opštoj formi koji iz konkretno
napravljene jednakosti 0 = 0, ne može dati ništa.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|