Rekao bih da zapravo važi

.

Ne razumijem kako dobiti rekurentnu formulu!?

Košijevim množenjem razvoja za tangens i kosinus i izjednačavanjem sa košijevim razvojem za sinus.

OK, vidim sve nešta jedva odgovori, samo me zanimalo kako se radi zadatak, jer ih ima dosta sličnih,
i ja sam izabrao ovaj primjer za foruma, nema veze . . .

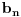
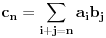
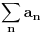
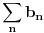
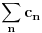
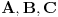
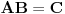
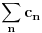
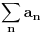
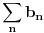
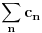
Teorema: Neka su i bilo kakvi nizovi i . Ako redovi , i konvergiraju ka vrednostima tim redom, onda je . Pritom je konvergencija reda mzagarantovana ako redovi i kovergiraju i pritom bar jedan od njih konvergira apsolutno. Ako oba konvergiraju apsolutno, onda i red konvergira apsolutno.

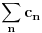
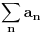
Definicija: Uz simboliku iz prethodne teoreme, red se zove Košijev proizvod redova i .

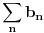
Košijev proizvod stepenih redova je stepeni red. Iz prethodne teoreme posebno sledi da je radijus konvergencije Košijevog proizvoda veći ili jednak od radijusa konvergencije činilaca.

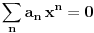
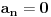
Teorema: Neka je za beskonačno mnogo vrednosti kojima je nula tačka nagomilavanja. Tada je . Odavde posebno sledi da ako dva stepena reda imaju istu sumu u takvom beskonačnom skupu tačaka, da onda imaju sve iste koeficijente i da ako je suma stepenog reda parna (neparna) funkcija, da su onda koeficijenti uz neparne (parne) stepene jednaki nuli.

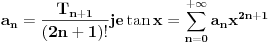
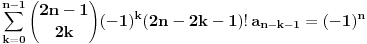
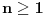
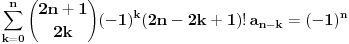
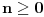
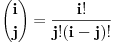
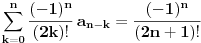
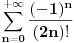
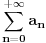
Da se vratimo na zadatak. Uz oznaku , a rekurentna formula koju treba dokazati je za , odnosno za . Korišćenjem jednakosti zaključuje se da je poslednja jednakost ekvivalentna sa , odnosno da je Košijev proizvod redova i jednak .

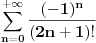
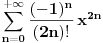
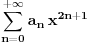
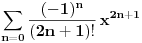
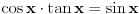
Dokazaćemo više, da je Košijev proizvod redova i jednak . Proizvod navedenih stepenih redova je stepeni red čija je suma , pa se taj Košijev proizvod poklapa sa razvojem sinusa. Za ovo je neophodno znati da je radijus konvergencije redova koji se množe veći od nule.

Drugi način da se reši zadatak je primena Lajbnicove formule o izvodima višeg reda proizvoda dve funkcije.