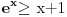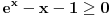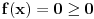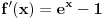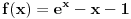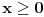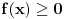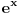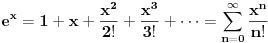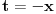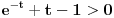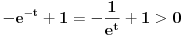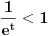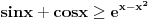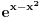[ ___ @ 09.02.2011. 14:17 ] @
|
[ Fermion @ 09.02.2011. 15:35 ] @
[ atomant @ 09.02.2011. 15:40 ] @
[ Fermion @ 09.02.2011. 15:47 ] @
[ ___ @ 09.02.2011. 16:37 ] @
Hvala vam.
Mada mene zapravo najviše i buni primena prvog izvoda tu. Šta za funkciju znači da je prvi izvod veći od nule, tj da je ona rastuća...može ona biti i rastuća, ali i da preseče x-osu negde, zar ne? Ili ja to ipak, baš uopšte, nisam dobro ukapirala? [ Fermion @ 09.02.2011. 16:44 ] @
Nula funkcije f(x) je u 0. Tu grafik te funkcije dodiruje x-osu. Za svako veće x od 0 funkcija je rastuća. Šta to znači? Što je nezavisna promenljiva x veća to je veća i vrednost funkcije. Dakle ako je nula funkcije u nuli, a za sve vrednosti veće od te funkcija raste, za svako x veće od 0 funkcija će imati veću vrednost nego u tački gde je jednaka nuli.
To je ideja. Slično se ispituje i kada je x<0. [ ___ @ 09.02.2011. 16:54 ] @
Ahaam...pa da, stvarno ima smisla. Hvala puno!
[ Fermion @ 09.02.2011. 16:54 ] @
Inače, smena iz mog drugog odgovora na ovoj temi nije neophodna, čak sam bez nekog potrebnog razloga učinio stvar težom za rešavanje. Evo prostije, za x<0
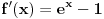 , što je manje od 0, pa je funkcija na tom intervalu opadajuća, tj. opada od neke vrednosti do 0, koja se dostiže za x=0, što znači da je za sve vrednosti manje od 0 veća od vrednosti u tački , što je manje od 0, pa je funkcija na tom intervalu opadajuća, tj. opada od neke vrednosti do 0, koja se dostiže za x=0, što znači da je za sve vrednosti manje od 0 veća od vrednosti u tački  , pri čemu , pri čemu 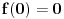 . . [ Fermion @ 09.02.2011. 17:01 ] @
Možda još prostiji način, koji neće baš uvek funkcionisati, ali prilično pojednostavljuje rešenje ove funkcije jeste nalaženje njenog ekstrema. Dakle nađemo prvi izvod:
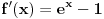 On je jednak nuli u tački gde je 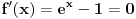 , tj. , tj. 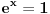 , što se postiže za , što se postiže za  . . Dakle funkcija ima samo jedan ekstrem, ali ne znamo da li je to maksimum ili minimum. Međutim, pošto je 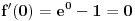 , a , a 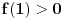 , sledi da je to minimum funkcije, što pokazuje da je polazno tvrđenje tačno. , sledi da je to minimum funkcije, što pokazuje da je polazno tvrđenje tačno. [ ___ @ 09.02.2011. 19:22 ] @
Hm, interesantno. Može li to eventualno da se primeni kada dokazujemo da fja ima jedinstvenu nulu? primera radi
[ Fermion @ 09.02.2011. 20:10 ] @
U nekim slučajevima verovatno da. Evo elementarnog primera
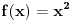 . Prvi izvod je . Prvi izvod je 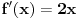 , a to je jednako nuli za x=0. Pošto je ekstrem u tački f(0)=0, a , a to je jednako nuli za x=0. Pošto je ekstrem u tački f(0)=0, a 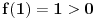 sledi da je funkcija za svako sledi da je funkcija za svako 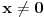 , tacnije gde , tacnije gde 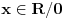 veća od nule. Pa je x=0 jedina nula ove funkcije. Dao sam lakši primer, ali uz malo kreativnosti trebalo bi da može i u nekim zahtevnijm zadacima primeniti. veća od nule. Pa je x=0 jedina nula ove funkcije. Dao sam lakši primer, ali uz malo kreativnosti trebalo bi da može i u nekim zahtevnijm zadacima primeniti.[ Sonec @ 30.01.2014. 13:59 ] @
[ miki069 @ 30.01.2014. 20:06 ] @
Koristi razvoj tih funkcije u Mekloranov polinom.
Uzmi prva tri ili četiri člana. [ NoSmoking95 @ 31.01.2014. 08:28 ] @
Aham, hvala. Vjerovatno se to tako radi. Nismo to radili na vježbama, tako da će zadatak sačekati. Hvala u svakom slučaju
[ petarm @ 04.03.2014. 07:30 ] @
Na okruznom za 4. razred gimnazije, B kategorija, ove godine je bio jedan zadatak iz ove oblasti. Pogledaj prvi zadatak za B kategoriju 4. razred.
http://srb.imomath.com/zadaci/2014_okruzno.pdf http://srb.imomath.com/zadaci/2014_okruzno_resenja.pdf Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|