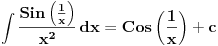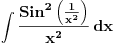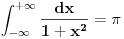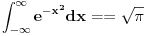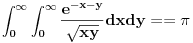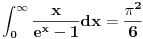[ de facto @ 09.02.2011. 19:10 ] @
| (1/x^2)sin^2(1/x^2)dx= Pokusavao sam smjenu da je 1/x=t i 1/x^2=t al ni jedna od tih ne odgovara da se dobije jednostavniji integral za rijestit, a rjesenje je cos1/x+c. Pokusavao sam rjesavnje na wolframalpha.com al ne daje rjesenje koje je u knjizi. hvala i pozdrav. |