Može se skratiti. I imenilac i brojilac su deljivi sa 3 za bilo koje n.

Da li je zadatak sigurno dobro napisan? Evo kako sam ga ja rastumačio:



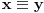
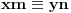
Iskoristimo jedno svojstvo kongruencija. Ako je i po modulu a, onda je po modulu a.

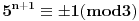
S obzirom da je , a , onda je za svako n jedan od pomenutih brojeva kongruentan 1, a drugi -1 po modulu 3.

To znači da je brojilac deljiv sa 3.

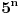
Kod imenioca se slično dobija da je isti deljiv sa 3, jer je jedan od brojeva i kongruentan jedan, drugi minus jedan, njihov proizvod uvek -1, a kada se doda 1, dobija se da je izraz u imeniocu deljiv sa 3.

Prema tome, razlomak je skrativ.

_{[Ovu poruku je menjao Fermion dana 10.02.2011. u 14:16 GMT+1]}