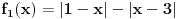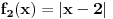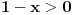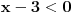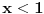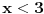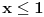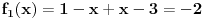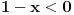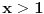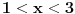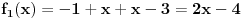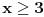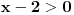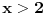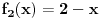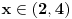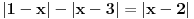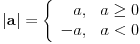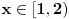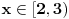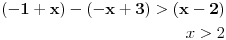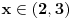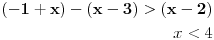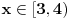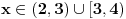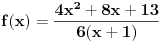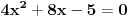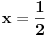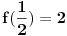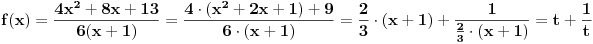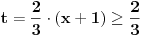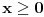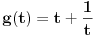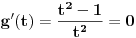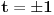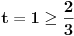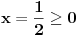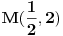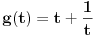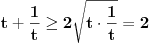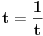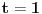[ Akycy @ 14.02.2011. 10:49 ] @
| Opet sam resavala onu nejednacinu |1-x|-|x-3|>|x-2| prvo ispitivala sam sve slucajeve tj imamo osam slucajeve i da bi imala resenje ja prikazem sve na brojevnoj pravo uslove i ona je definisana kada su svi uslovi veci od nulu ili manji od nule ali nije mi jasno kod treceg uslova kad dobijem da dva uslova imaju zajednicku vrednost a ovaj treci suprotno od njih preseca ova druga dva pa nikako ne mogu da skontam u kojoj je ralaciji x definisano molila bih za pomoc kako da odredim tu relaciju i valjda mi zbog toga ne ispada kao u resenje. |