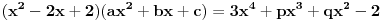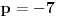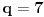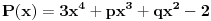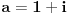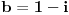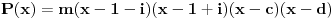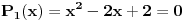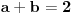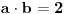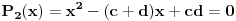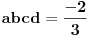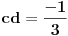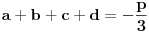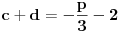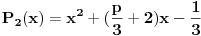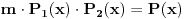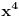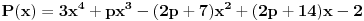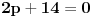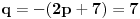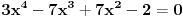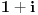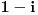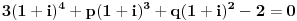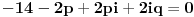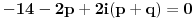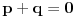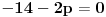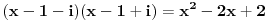[ mladen.rad @ 15.02.2011. 01:45 ] @
| Ovako,zadatak glasi: dat je polinom P(x)=3x^4+px^3+qx^2-2 , p,q e R treba odrediti p i q tako da je x1=1+i jedna nula i treba odrediti ostale nule. Ovako ja sam pokusao ovako,rekao sam da je 1+i resenje kvadratne jednacine i nasao sam je x^2-2x+2 ta jednacina.Druga nula bi bila 1-i. Onda za te dve nule primenim bezuov stav i dobijem da su i p i q kompleksni brojevi i dalje ne znam sta da radim,verovatno gresim. Da li je to pravi nacin da se resi zadatak? |