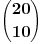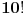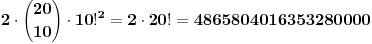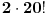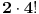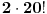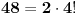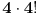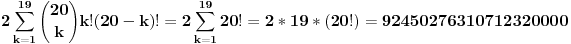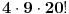|
|
[ zijadic91 @ 15.02.2011. 13:16 ] @
|
| Nikako nemogu ovo da resim nemam cak ni ideju
kako da pocnem zadatak je sledeci
Dvadesetoro ucenika jednog odeljenja dobili su zadatke 2 grupe jedne pismene vezbe.Na koliko nacina se oni mogu poredjati u 2 reda tako da dvoje,koji sede jedan do drugog,dobijaju razlicite grupe,a svi koji su jedan iza drugog,iste grupe.Unapred zahvalan.! |
[ Nedeljko @ 15.02.2011. 16:21 ] @
Imaš dve šeme rasporeda grupa u učionici - onu kod koje najlevlji učenik u redu ima zadatke prve grupe i onu u kojoj najlevlji učenik u redu ima zadatke druge grupe.
Zatim imaš 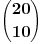 načina da izabereš koji će učenici imati zadatke prve grupe.
Napokon, učenike svake grupe možeš da permutuješ na 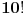 načina.
Znači, ukupan broj mogućnosti je 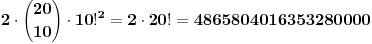 . [ zijadic91 @ 15.02.2011. 17:00 ] @
izvinjavam se ali nije mi jasno bas najbolje.I kako pise na resenju
2*(20!)^2 ne sumnjam u vasu strucnost ali kako je to moguce.
[ Nedeljko @ 15.02.2011. 20:03 ] @
U rešenjima često ima grešaka. Probaj ručno da rasporediš na primer 4 učenika na sve moguće načine. Po mojoj računici ima 2*4!=48 načina. Ako nađeš više (prema njihovom rešenju ima 2*4!2=1152) onda sam ja nešto zeznuo (mada, i dalje stojim iza svog rešenja), onda su oni zeznuli.
Pazi, ovako. Da rasporediš 2n učenika na 2n stolica možeš na (2n)! načina i posle svakome da daš zadatak iz jedne od grupa možeš na 22n načina. Dakle, bez ikakvih dodatnih ograničenja, to je 22n(2n)! mogućnosti, a sa ograničenjima iz zadatka ih ima manje. 244!=384, pa rasporeda sa dodatnim ograničenjima iz zadatka svakako ne može biti 2*4!2=1152.
[ zijadic91 @ 15.02.2011. 21:08 ] @
Zar cetiti ucenika nemozes da rasporedis na 4!=24 nacina
[ Fermion @ 15.02.2011. 21:19 ] @
Kada je učenika 20, onda je po Nedeljkovom rešenju:
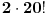
Kada ih je 4 po analogiji:
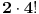
[ Nedeljko @ 15.02.2011. 21:19 ] @
Da, pa?
[ Fermion @ 15.02.2011. 21:29 ] @
Meni se čini Nedeljkovo rešenje dobrim. Radio sam ovaj zadatak već ranije i nisam ni ja mogao da dobijem rezultat iz rešenja, već upravo ovo. Samo tada sam zaključio da nisam dobro razumeo zadatak  . [ Sini82 @ 15.02.2011. 22:20 ] @
Nedeljko je u pravu. Rješenje je 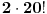 .
Raspisao sam za 4 učenika, ima 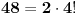 mogućih slučajeva. [ MajorFatal @ 16.02.2011. 06:23 ] @
Da li mogu da se rasporede u 2 reda tako sto je u prvom redu samo 1 ucenik a u drugom preostalih 19? Pise da dvoje koji sede jedno do drugog moraju imati zadatke razlicitih grupa a ne da pod obavezno sede po dvoje u klupi? Pa onda 2-18, 3-17 .. itd...
Da je trebalo da se podeli u 2 reda po 10 ucenika to bi pisalo u postavci?
[Ovu poruku je menjao MajorFatal dana 16.02.2011. u 07:36 GMT+1]
[ Sini82 @ 16.02.2011. 13:27 ] @
@MajorFatal
Kada sam raspisivao za četiri učenika, to mi nije igralo ulogu. Pretpostavio sam da u svakoj klupi sjedi jedan učenik. Tu sam pogriješio, učenici sjede u klupama po dvoje. U tom slučaju ima 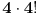 mogućih rasporeda mogućih rasporeda. U pravu si, nigdje u zadatku ne piše da u oba reda mora da bude isti broj klupa, možda je rješenje u knjizi tačno.
[Ovu poruku je menjao Sini82 dana 16.02.2011. u 14:44 GMT+1]
[ MajorFatal @ 16.02.2011. 18:13 ] @
E, e, moja greska, sede u amfiteatru zar ne? I to jedan do drugog, pa grupe moraju da budu rasporedjene naizmenicno onima koji sede jedan do drugog do kraja reda?
[ edisnp @ 16.02.2011. 21:00 ] @
Ne mora da znaci ako pise u zadatku da dvoje koji sede jedan do
drugog dobiju razlicite grupe to ne znaci da sede u istoj klupi.
[ zijadic91 @ 18.02.2011. 15:43 ] @
pa koje je onda tacno resenje
[ Nedeljko @ 18.02.2011. 17:51 ] @
Da bi se na to pitanje odgovorilo, mora se prvo znati šta je tačna postavka.
[ MajorFatal @ 18.02.2011. 19:36 ] @
Ala ste Vi matematicari skrti na recima I na formulama. Ovako kako si postavio zadatak verovatno ti je najtacnije ono sto ti je Nedeljko napisao.
Ali moram nesto da pitam u vezi sa tim resenjem: nacin izbora “20 nad 10” podrazumeva da smo vec prebrojli sve mogucnosti da neki ucenik resava zadatke i jedne i druge grupe? tj. ako odaberemo prvih 10 ucenika za prvu grupu (ili zadatke za ucenike) u sledecem biranju mozemo da biramo istih 9 recimo, ali bar jedan mora da zavrsi u drugoj grupi tj. vec je “vidjen” (prebrojan) da resava zadatke druge grupe, u nekim od sledecih izbora 2 ili vise ucenika tj. do kraja svi, da li to znaci da smo vec “prebrojali” mogucnosti da svi ucenici rade zadatke iz obe grupe, tj. da je dovoljna 1 distribucija zadataka kad vec poredjamo ucenike u grupe i u redove? tj. da je ono 2* na pocetku racuna suvisno? Pitam jer ne bih voleo da mi se desi da brojim kombinacije koje sam vec prebrojao?
Da li moze ovako:
Po postavci: zadaci su vec podeljeni ucenicima i vec su formirane 2 grupe ucenika pa tu nista ne moramo da racunamo osim da pretpostavimo da su grupe po broju ucenika jednake? Sad samo treba poredjati te dve grupe ucenika u dva reda ali tako da uvek onaj koji sedi ispred resava istu grupu a onaj “do” tj sto sedi sa strane da resava razlicitu? I poredjas ih lepo na jedini moguci nacin a koga je komada jedan: sedite u 1 red Vi iz prve grupe a u 2 red Vi iz druge grupe? Odnosno ovih nacina ima dva, mogu ovi iz prve grupe da sede u redu levo ili desno. Ovde podrazumevamo klasicnu osnovnoskolsku/srednjskolsku ucionicu sa 1 redom klupa, onih duplih gde po dva ucenika mogu da sede u klupi pa bi se 2 reda sa istim brojem ucenika formirala od table prema suprotnom zidu, a to sto ima dve grupe i sto ovi iz iste grupe sede jedan iza drugog a ovi iz razlicite jedno do drugog to bi kao trebalo da obezbedi da ne prepisuju. I nema spajanja klupa :) mada niko nije rekao ni da ima tako da profesor moze da proseta izmedju redova. kojih takodje nema :) jer se u postavci pominje samo 2 reda ucenika ali ne i dva reda klupa, i onda samo izmnozim broj kombinacija bez ponavljanja za obe grupe tj. br rasporeda kako mogu da sede po redovima tj. da ne menjaju grupu i to je 10! * 10! = 10!^2. I puta one dve kombinacije na pocetku za raspored grupa u redove levo – desno: =2*(10!)^2? I neko pogresio u prepisivanju ili slovoslagac u slovoslaganju i eto ti resenje iz zbirke? :) lici: 2*(20!)^2? razlikuje se samo za 1 cifru? :)
[ kandorus @ 19.02.2011. 02:12 ] @
Mora da se množi sa 2 jer kad se sastave svi redovi, od kojih neki imaju zadatke prve grupe a drugi zadatke druge grupe, opet mogu da se sastave isti redovi ali sa obrnutim grupama zadataka.
Kako ste dobili da grupe imaju tačno po 10 učenika? U zadatku to ne piše.
Prvi red može da ima od k = 1, 2, ..., 19 učenika, učenici drugog reda, njih (20 - k), jednoznačno su odredjeni izborom prvog reda.
20 učenika se može deliti u grupe od po k i (20 - k) učenika na 20!/(k!*(20-k)!) načina.
Dalje se k učenika prvog reda mogu ispermutovati na k! načina.
Isto tako se (20 - k) učenika drugog reda mogu ispermutovati na (20 - k)! načina.
Najzad postoje dve grupe zadataka pa se sve množi sa 2.
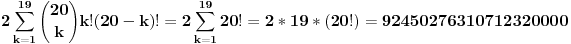
[ kandorus @ 19.02.2011. 06:12 ] @
Citat: kandorus: Mora da se množi sa 2 jer kad se sastave svi redovi, od kojih neki imaju zadatke prve grupe a drugi zadatke druge grupe, opet mogu da se sastave isti redovi ali sa obrnutim grupama zadataka.
Ne mogu jer na pocetku zadatka pise "ucenicima su podeljene 2 grupe zadataka", znaci vec su formirane grupe pa nema smisla racunati sta bi bilo kad bi svi oni radili zadatke i iz druge grupe jer se to nece desiti?
Citat: kandorus:
Kako ste dobili da grupe imaju tačno po 10 učenika? U zadatku to ne piše.
Pa ne pise ni da redovi mogu imati minimalno 1 maksimalno 19 clanova? Kako si ti to dobio? Na primer izvlace zadatke sa gomile i svi izvuku istu grupu?
Citat: kandorus:
Prvi red može da ima od k = 1, 2, ..., 19 učenika, učenici drugog reda, njih (20 - k), jednoznačno su odredjeni izborom prvog reda.
Istim principom je jednoznacno odredjeno i koju grupu zadataka ce raditi? Onu koju su dobili na pocetku?
Citat: kandorus:
20 učenika se može deliti u grupe od po k i (20 - k) učenika na 20!/(k!*(20-k)!) načina.
Dalje se k učenika prvog reda mogu ispermutovati na k! načina.
Isto tako se (20 - k) učenika drugog reda mogu ispermutovati na (20 - k)! načina.
Najzad postoje dve grupe zadataka pa se sve množi sa 2.
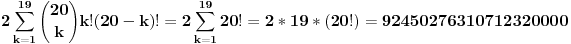
Mislim da je ovo sini82 izracunao, ali tacno, pre 6 postova? Za 4 ucenika koji ne mora da znaci ako pise u zadatku da dvoje koji sede jedan do
drugog dobiju razlicite grupe to ne znaci da sede u istoj klupi, ali ipak sede tako, to je: 4*4! u tvom slucaju 20*20!?
Ipak cu ponovo pitati ovo sto mene zanima: Cak i ako bi se zadaci naknadno delili po formiranju redova da li nacinom izbora "20 nad 10" vec prebrajamo sve situacije u kojima bilo koji ucenik spada u jednu ili drugu grupu pa nam onda ne treba obe distribucije zadataka po grupama nego samo 1 tj. ne treba da se mnozi sa dva? Meni ponudjeni odgovor vise lici na odgovor na pitanje: sve ono sto je vec pitano + ali tako da 1 cas rade zadatke iz jedne grupe a sledeci cas iz druge, na primer? [ Sini82 @ 19.02.2011. 10:44 ] @
Ako sjede u klupama po dvoje, onda mogu da se rasporede na 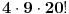 načina. [ kandorus @ 19.02.2011. 11:29 ] @
^Gost
Posmatraj sledeću raspodelu 4 učenika:
12
34
Njima zadaci mogu biti dodeljeni na sledeči način:
1a 2a
3b 4b
1b 2b
3a 4a
pa broj kombinacija učenika se množi sa brojem grupa zadataka, tj. 2.
Citat: Pa ne pise ni da redovi mogu imati minimalno 1 maksimalno 19 clanova?
Ne kažem da piše ali pošto zadatkom to nije odredjeno mogu da pretpostavim, isto kao što su drugi pretpostavili da ima tačno 10.
Posle ovolike diskusije čini mi se da je zadatak neprecizno postavljen. Mogao sam na primer da pretpostavim da se nizovi ne razlikuju (u smislu onaj do prozora i onaj do vrata) pa tada k = 1, 2, ..., 10 i dobije se rešenje 48658040163532800000.
Citat: Ipak cu ponovo pitati ovo sto mene zanima: Cak i ako bi se zadaci naknadno delili po formiranju redova da li nacinom izbora "20 nad 10" vec prebrajamo sve situacije u kojima bilo koji ucenik spada u jednu ili drugu grupu pa nam onda ne treba obe distribucije zadataka po grupama nego samo 1 tj. ne treba da se mnozi sa dva?
Izbor "20 nad 10" ne sadrži informaciju ni o čemu drugom osim o broju načina na koji se može izabrati delegacija od po 10 iz skupa od 20 elemenata. Elementi se ne razlikuju ni na koji način osim što je poznata kardinalnost skupova. Moglo je da bude i 3 grupe zadataka pa šta tad?
Obrati pažnju šta piše u zadatku:
Citat: tako da dvoje,koji sede jedan do drugog,dobijaju razlicite grupe
Dakle prvo se učenici podele po redovima a zatim se dele zadaci. Nema sumnje da se zadaci dele na dva načina.
[ kandorus @ 20.02.2011. 02:57 ] @
Zadatak je bezveze al mi volimo da trabunjamo o resenjima i u slobodno vreme...
Ono sto si napisao je tacno ako je ucionica na bilo koji nacin orijentisana tj. ima tablu, vrata, profesora, tebe, ako nema a dobro si primetio da se u zadatku ne pominju ni prozori ni suprotni zid od table red "orijentisu" sami ucenici jer oni znaju sta im je ispred a sta iza i levo i desno?
na primer :
4b 3b
2a 1a
tebi ce se sigurno ciniti da je to jos jedna kombinacija za prebrojati od mogucih 48, ali to je ona ista situacijaa koju si ti prvo naveo ali suprotno orijentisana, to je zato sto ti na situaciju gledas sa strane kao nepristasan posmatrac, medjutim posto svi ucenici u ovoj situaciji gledaju na desno, na primer dvojka bi mogla reci cetvorci: kec ispred, trojka levo, ti dijagonalno...pa mi smo vec bili u ovom rasporedu i resavali ove zadatke? Na sta bi cetvorka odgovorila: Da, nadam se da tip koji broji ove kombinacije pazi sta radi, inace bi po 49736-ti put bili u istoj poziciji i resavali iste zadtke? Tj. za ovaj zadatak kao i za vecinun ostalih mora da postoji neki referentni sistem makar to bio ti ili tabla?
Ostavicu tebi da nadjes jos 2 situacije u kojima dvojka moze da kaze ovo isto a cetvorka da potvrdi...
[ kandorus @ 20.02.2011. 04:09 ] @
Član  garantuje da je svaki podskup izabran tačno jednom (kombinacije su neuredjeni skupovi). Uredjivanje u nizove se vrši permutacijama čiji broj odredjuju članovi k! i (n - k)!. Kako su permutacije bijekcija skupa na samog sebe nema opasnosti da se neki redosled pojavi više puta. [ MajorFatal @ 21.02.2011. 00:49 ] @
Hvala! Sad je malcice jasnije, znaci samo je bitan broj mogucih pozicija? A sta se desava ako bi imali neko mesto viska tipa: 12 klupa sa po dva mesta i 20 ucenika? Svi razliciti rasporedi sedenja? Zaboravih da se ulogujem prethodna 2 puta...
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|