[ kakosuper @ 27.02.2011. 18:43 ] @
| Posto nisam nasao nigde na netu, reko aj da pitam i ovde. Da li neko zna da mi objasni sta su furijeovi brojevi, i sta je to beselova nejednakost? Stvarno mi mnogo treba a nikako nigde ne mogu naci.. :( |
|
[ kakosuper @ 27.02.2011. 18:43 ] @
[ petarm @ 27.02.2011. 19:30 ] @
Furijeovi brojevi bi trebalo da budu Furijeovi koeficijenti pretpostavljam?
Beselova nejednakost ti je 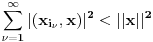 gde su 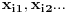 elementi ortonormiranog sistema elementi ortonormiranog sistema 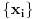 za koje su koeficijenti nekog elementa za koje su koeficijenti nekog elementa 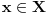 razliciti od nule. razliciti od nule. ti je unitarni prostor, tj. prostor u kojem je definisan skalarni proizvod, a ti je unitarni prostor, tj. prostor u kojem je definisan skalarni proizvod, a 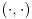 je oznaka koju sam koristio za skalarni proizvod u datom zapisu. je oznaka koju sam koristio za skalarni proizvod u datom zapisu.[ kakosuper @ 27.02.2011. 20:28 ] @
Aham znaci ako sam nekako shvatio, to je skup skalarnih proizvoda elemenata ortonormiranog sistema?
Da na furijeove koeficijente sam mislio? Dal mi mozes nesto reci sta su oni i cemu sluze? :) [ edisnp @ 27.02.2011. 22:10 ] @
Odredjivanje koeficienata a0,an,bn uslovljeni su razvojem funkcije u furijeov red ,tj.
razvoj funkcije u furijeov red svodi se na odredjivanje koeficienata a0,an,bn.Dok se za odredjivanje furijeovih koeficienata koristi osobina ortogonalnosti funkcije cosx,cos2x sinx,sin2x. [ ~stojko~ @ 28.02.2011. 00:12 ] @
Citat: kakosuper: Da na furijeove koeficijente sam mislio? Dal mi mozes nesto reci sta su oni i cemu sluze? :) U elektrotehnici mnogi od signala su periodični. (Tocnije priblizno periodicni.) Periodičan signal može sadržavati samo jednu frekvenciju. Tada je to sinusni signal. Neki to zovu i kosinusni signal, ali cinjenica da je u pitanju jedna frekvencija nece se time promijeniti. Fazni pomak signala privremeno recimo da nije bitan. Signal koji sadrži samo jednu frekvenciju postoji samo u matematici. U elektrotehnici uvijek su u signalu prisutne i druge frekvencije. Kada su druge frekvencije zanemarive amplitude tj. pripadni Fourierov koeficijent zanemarivo malen kazemo da je u pitanju cisti sinusni signal. Kada druge frekvencije nisu zanemarive amplitude ... e ponekad se kaže da je signal izobličen, jer tada ga uspoređujemo s čistim sinusnim. Frekvencije se nazivaju harmonici. Izobličenja koja spomenuh nazivaju se harmonička. Iznos Fourierovih koeficijenata dakle govori o količini izobličenja ili tocnije o razlici promatranog periodickog signala i nekog drugog referentnog periodickog signala. Naravno, Fourierovi koeficijenti imaju upotrebu i izvan elektrotehnike ... Odlicna stranica s primjerima utjecaja promjene amplitude harmonika na valni oblik signala: http://www.falstad.com/mathphysics.html [ Nedeljko @ 28.02.2011. 10:06 ] @
Neka je
 neprazan skup (zvaćemo ga skupom vektora) i neka je data binarna operacija neprazan skup (zvaćemo ga skupom vektora) i neka je data binarna operacija 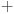 nad elementima tog skupa, koja ima uobičajene osobine, kao npr. sabiranje realnih brojeva. Recimo, postoji neuralni element i svakom elementu postoji suprotan, tako da elementa u zbiru sa svojim suprotnim elementom daje neutralni element i neka važe zakoni nad elementima tog skupa, koja ima uobičajene osobine, kao npr. sabiranje realnih brojeva. Recimo, postoji neuralni element i svakom elementu postoji suprotan, tako da elementa u zbiru sa svojim suprotnim elementom daje neutralni element i neka važe zakoni 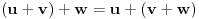 i i 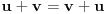 . Preciznije, pretpostavlja se da za elemente tog skupa važe sledeći zakoni: . Preciznije, pretpostavlja se da za elemente tog skupa važe sledeći zakoni: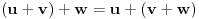 , ,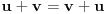 , ,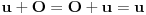 , ,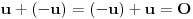 , ,gde smo sa  označili neutralni element (koji uzgred pripada skupu označili neutralni element (koji uzgred pripada skupu  ), a sa ), a sa 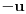 suprorotan element od elementa suprorotan element od elementa  . Neka je data i operacija množenje vektora realnim (odnosno kompleksnim) brojevima tako da ako brojeve označimo grčkim, a vektore latiničnim slovima, važe sledeći zakoni . Neka je data i operacija množenje vektora realnim (odnosno kompleksnim) brojevima tako da ako brojeve označimo grčkim, a vektore latiničnim slovima, važe sledeći zakoni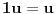 , ,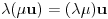 , ,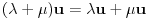 , ,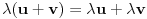 . .Tada kažemo da je skup  snabdeven ovim operacijama realan (odnosno kompleksan) vektorski prostor. snabdeven ovim operacijama realan (odnosno kompleksan) vektorski prostor.Ako je pritom data jedna binarna operacija 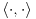 koja parovima vektora pridružuje realne (odnosno kompleksne) brojeve (koje zovemo i skalarima) tako da su ispunjeni sledeći uslovi: koja parovima vektora pridružuje realne (odnosno kompleksne) brojeve (koje zovemo i skalarima) tako da su ispunjeni sledeći uslovi: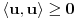 (dakle, (dakle, 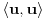 mora biti realan nenegativan broj, čak i ako smo uzeli kompleksne brojeve kao skalare). mora biti realan nenegativan broj, čak i ako smo uzeli kompleksne brojeve kao skalare).Ako je 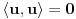 , onda je , onda je 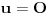 . .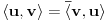 ("nadvučeno" je ovde oznaka za kompleksni konjugat. U realnom slučaju se to naravno svodi na ("nadvučeno" je ovde oznaka za kompleksni konjugat. U realnom slučaju se to naravno svodi na 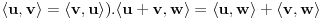 , ,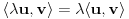 . .Za 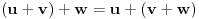 i i 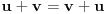 Tada takvu operaciju zovemo skalarnim proizvodom. Za vektore se kaže da su ortogonalni ako im je skalarni proizvod jednak nuli. Ako je 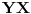 sistem uzajamno ortogonalnih vektora, među kojima se ne nalazi sistem uzajamno ortogonalnih vektora, među kojima se ne nalazi  i i  bilo koji vektor, se za broj bilo koji vektor, se za broj 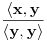 kaže da je Furijeov koeficijent vektora kaže da je Furijeov koeficijent vektora  po vektoru po vektoru 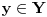 , a za formalan red , a za formalan red 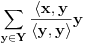 da je Furijeov red vektora da je Furijeov red vektora  po sistemu po sistemu  . .U svakom slučaju, 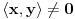 za najviše prebrojivo mnogo za najviše prebrojivo mnogo 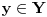 i pritom je i pritom je 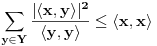 . To je Beselova nejednakost. Pritom jednakost važi za sve moguće vektore . To je Beselova nejednakost. Pritom jednakost važi za sve moguće vektore 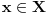 ako i samo ako je ako i samo ako je  maksimalan ortogonalan podskup od maksimalan ortogonalan podskup od  (koji ne uključuje (koji ne uključuje  ). ).Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|