[ jovannk @ 28.02.2011. 08:51 ] @
| Zad: Odrediti max broj [Ovu poruku je menjao jovannk dana 02.03.2011. u 01:47 GMT+1] |
|
[ jovannk @ 28.02.2011. 08:51 ] @
[ Sini82 @ 28.02.2011. 17:05 ] @
[ jovannk @ 28.02.2011. 22:34 ] @
Hvala, Sini. I ja sam dosao do ove formule al sam slabo postavio pitanje..
[Ovu poruku je menjao jovannk dana 02.03.2011. u 01:40 GMT+1] [Ovu poruku je menjao jovannk dana 02.03.2011. u 01:45 GMT+1] [ jovannk @ 01.03.2011. 08:01 ] @
Hvala. Ima li ko ideju moze li preko faktorijela, lici mi da moze al sam se zapetljao
[ atomant @ 01.03.2011. 08:35 ] @
Pa ako je zadatak da napises program onda ti je ova formula sasvim dovoljna za iterativnu proceduru. Ako ga pakujes na faktorijel moze da se uradi i preko rekurzije, ali rekurzija je uvek sporija jer funkcija poziva sama sebe vise puta. Je l' mnogo bitno da bude u obliku faktorijela?
[ jovannk @ 01.03.2011. 08:50 ] @
Zbog -1/6 se moze dobiti negativan broj a broj kv. matrica bi valjda trebao da je cio pozitivan broj, i valjda k ide od 0 do m-1).
[Ovu poruku je menjao jovannk dana 02.03.2011. u 09:07 GMT+1] [ SrdjanR271 @ 01.03.2011. 15:31 ] @
[ SrdjanR271 @ 01.03.2011. 19:29 ] @
[ jovannk @ 01.03.2011. 22:33 ] @
[ SrdjanR271 @ 02.03.2011. 00:01 ] @
Da ono je formula za Sinijevu sumu do m-1.
Ja sam to izracunao u Mathematici nisam rucno. A mozes (moras) da koristis te sume za sumu kvadrata i sumu prirodnih brojeva. Kad primenis te formule, jel dobijes ovako nesto 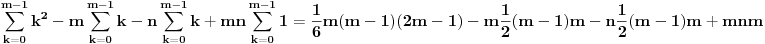 Kad sve izmnozis i izvuces m (ili prvo izvuces m) dobices kao ja. 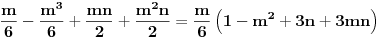 Mozda te je bunilo ovo 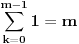 [ jovannk @ 02.03.2011. 00:13 ] @
[ miki069 @ 02.03.2011. 00:28 ] @
Konkretno za m=10.
Koliko je 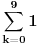 ? ?1+1+1+1+1+1+1+1+1+1 = 10. Odnosno m u opštem slučaju. Zadatak ti je urađen ispravno ako je glasio: "Odrediti max broj kvadratnih matrica u matrici reda mxn (m-kolone, n-redovi i n>m)." Bez onog čudnog dela dela: "gdje se kvadratnom matricom smatra i jedinični član uz krajnju ivicu". Računati su i svi elementi (1X1) koji i nisu uz krajnu ivicu, što je i normalno i tako je Sini82 i uradio. [Ovu poruku je menjao miki069 dana 02.03.2011. u 01:41 GMT+1] [Ovu poruku je menjao miki069 dana 02.03.2011. u 01:56 GMT+1] [ jovannk @ 02.03.2011. 00:37 ] @
[ miki069 @ 02.03.2011. 01:08 ] @
Kada bi se od ovih tvojih kvadratnih podmatrica tipa 1X1, 2X2, 3X3... izračunale determinante one se zovu Minori.
Ali ovu su samo minori nastali ukrštanjem susednih vrsta i susednih kolona. Definicija: Minor reda k matrice AmXn je vrednost determinante kvadratne podmatrice tipa kXk, nastale iz matrice A ukrštanjem bilo kojih njenih k vrsta i k kolona. k=1,2,3...min(m,n). Dakle minori tipa 2 nisu samo od kvadratnih podmatrica nastalih ukrštanjem 2 susedne vrse i 2 susedne kolone, već bilo koje 2 vrste i 2 kolone. Recimo može (1 i 3) vrsta ukrštene sa (2 i 5) kolonom i broj minora je daleko veći od ovog što su tebi izračunali. Ti si dobio broj minora u "komadu". Jedino se ne menja kod minora tipa 1X1. Zadatak se generalizuju na: "Koliko ima minora tipa 2, tipa 3.... do tipa min(m,n)". Možemo uzeti da je min(m,n) = m. Znao bih da napišem program da ih sve izgeneriše, ali mi prebrojavanje zapinje. [ SrdjanR271 @ 02.03.2011. 02:42 ] @
@Miki069
Jesi na ovo mislio? Citat: Let A be an m × n matrix and k an integer with 0 < k ≤ m, and k ≤ n. A k × k minor of A is the determinant of a k × k matrix obtained from A by deleting m − k rows and n − k columns. Since there are: 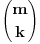 ways to choose k rows from m rows, and there are 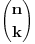 ways to choose k columns from n columns, there are a total of 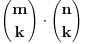 minors of size k × k. Izvor http://en.wikipedia.org/wiki/Minor_%28linear_algebra%29 [ miki069 @ 02.03.2011. 08:37 ] @
To je to.
Toliko je jasno iz dela definicije "...ukrštanjem bilo kojih njenih k vrsta i k kolona.." da mi sad nije jasno šta sam ja muljao i komplikovao. U programu i koristim generator kombinacija, a u prebrojavanju nisam ukapirao da su kombinacije. Hvala Srdjane. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|