Uvrsti i po formuli pa ćeš vidjeti da vrijedi jednakost . Rastavi kvadratni trinom na činioce (nadopunjavanjem na potpuni kvadrat), doći ćeš do formule za i navedene jednakosti.

Samo da probam [t e x]a(x-x1)(x-x2)[\ t e x]
opet neumem zbog cega nece

Ne to levo, drugo levo, tj. ne \tex nego /tex

Postoji opšti stav o euklidskom delenju polinoma, preko koga se ovakve stvari dokazuju.

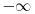
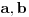
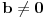
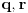
Smatraćemo da je stepen konstantnog ne-nula polinoma jednak nuli, a stepen nula polinoma jednak . Za ma koje polinoma , pri čemu je postoji tačno jedan par polinoma takvih da je stepen polinoma manji od stepena polinoma i da važi jednakost .

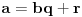
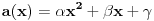
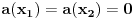
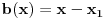
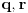
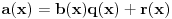
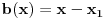
Recimo da je i da je . Za postoji tačno jedan par polinoma takvih da je i tako da je stepen polinoma manji od stepena polinoma , koji je jednak . Stoga mora biti konstantan polinom, pa je

,

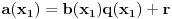
odnosno

,

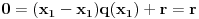
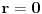
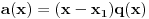
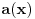
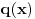
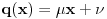
odakle je , a samim tim i . Obzirom da je polinom stepena najviše dva, lako se zaključuje da je polinom stepena najviše jedan, tj. da je . Iz



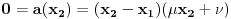
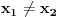
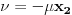
uz pretpostavku sledi da je , a samim tim i

.

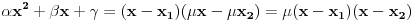
Izjednačavanjem vodećih koeficijenata zaključujemo da je .
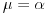