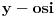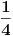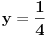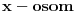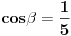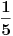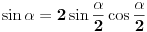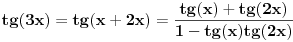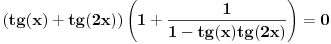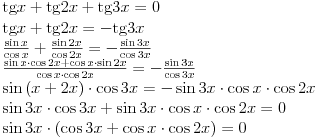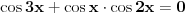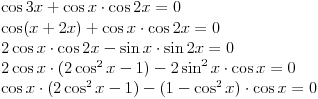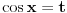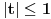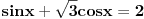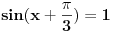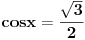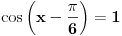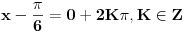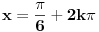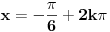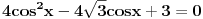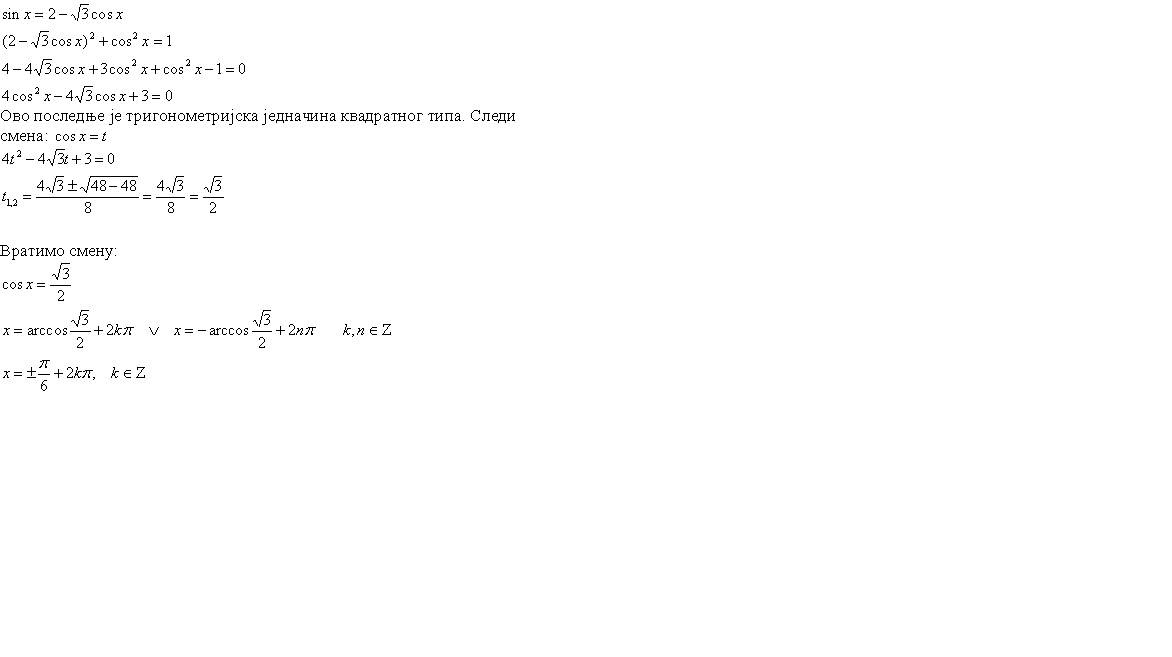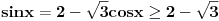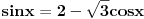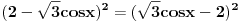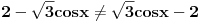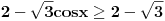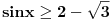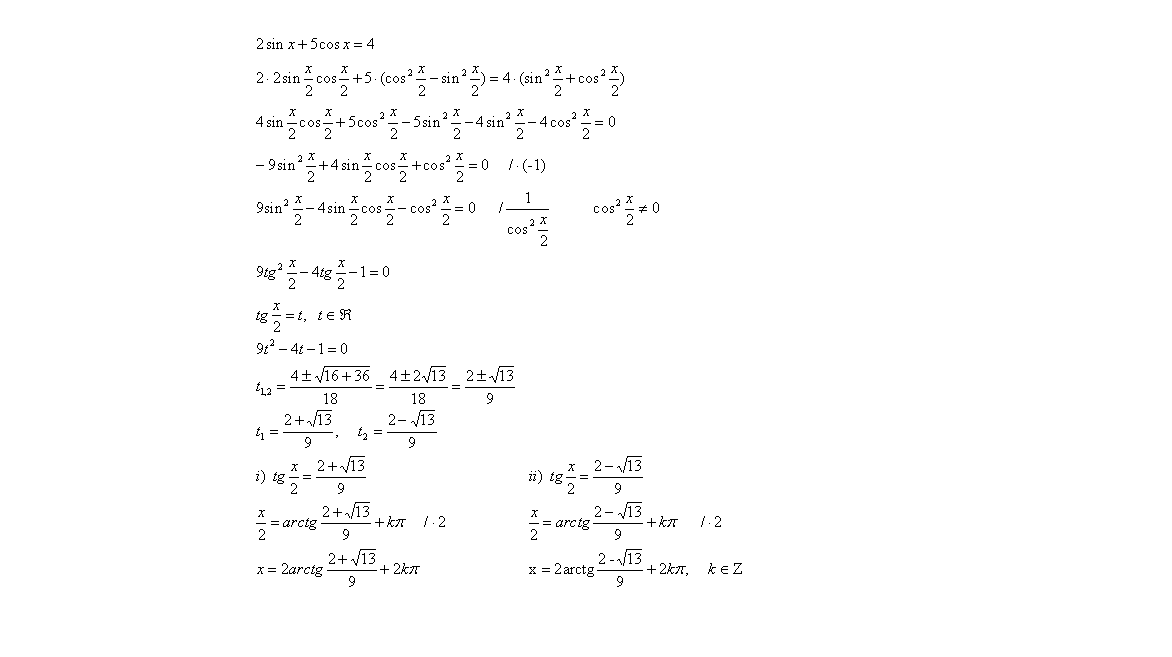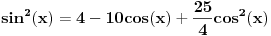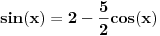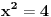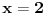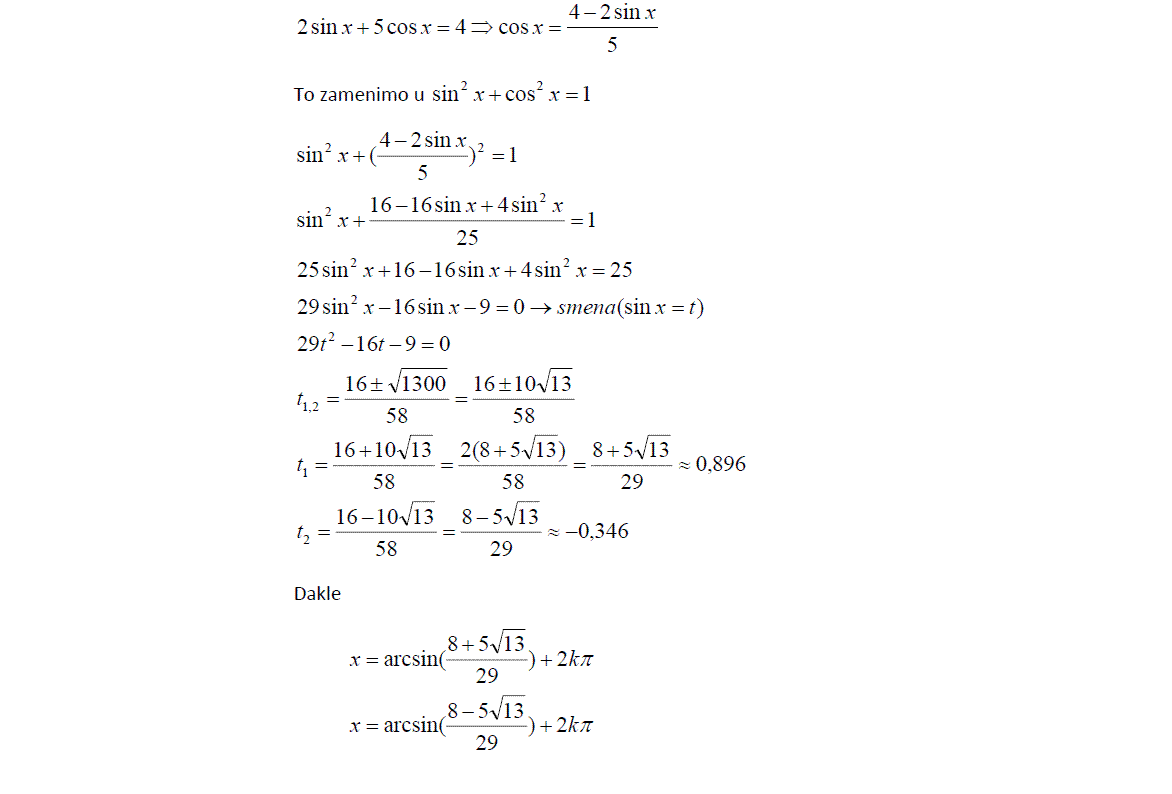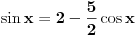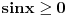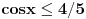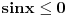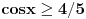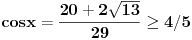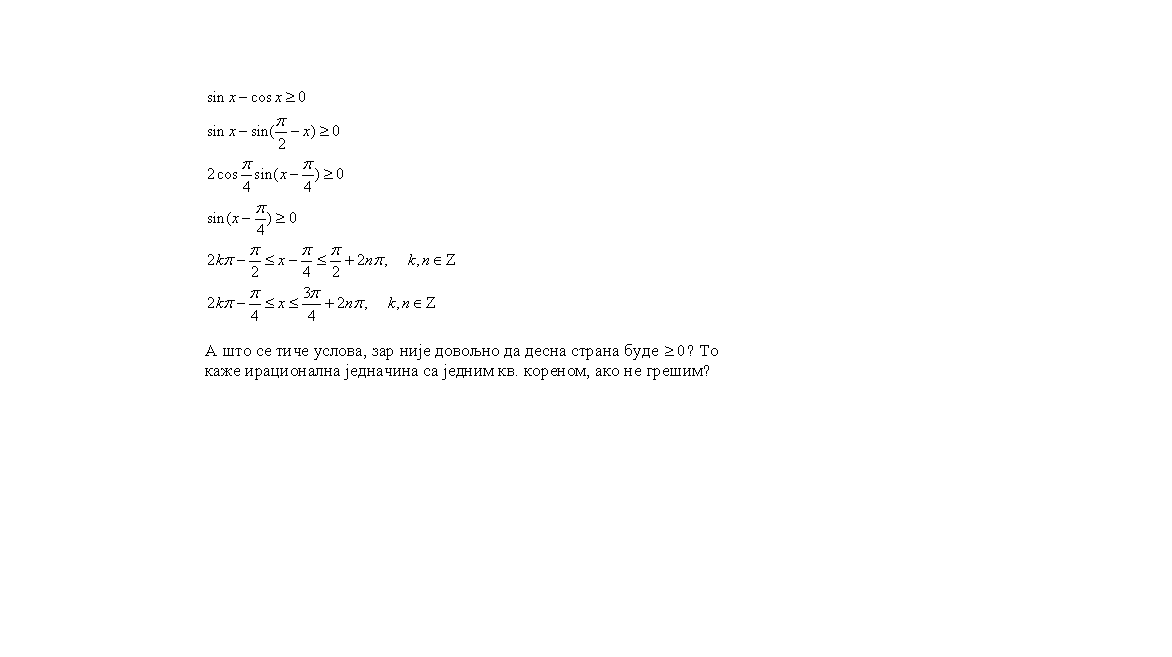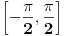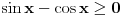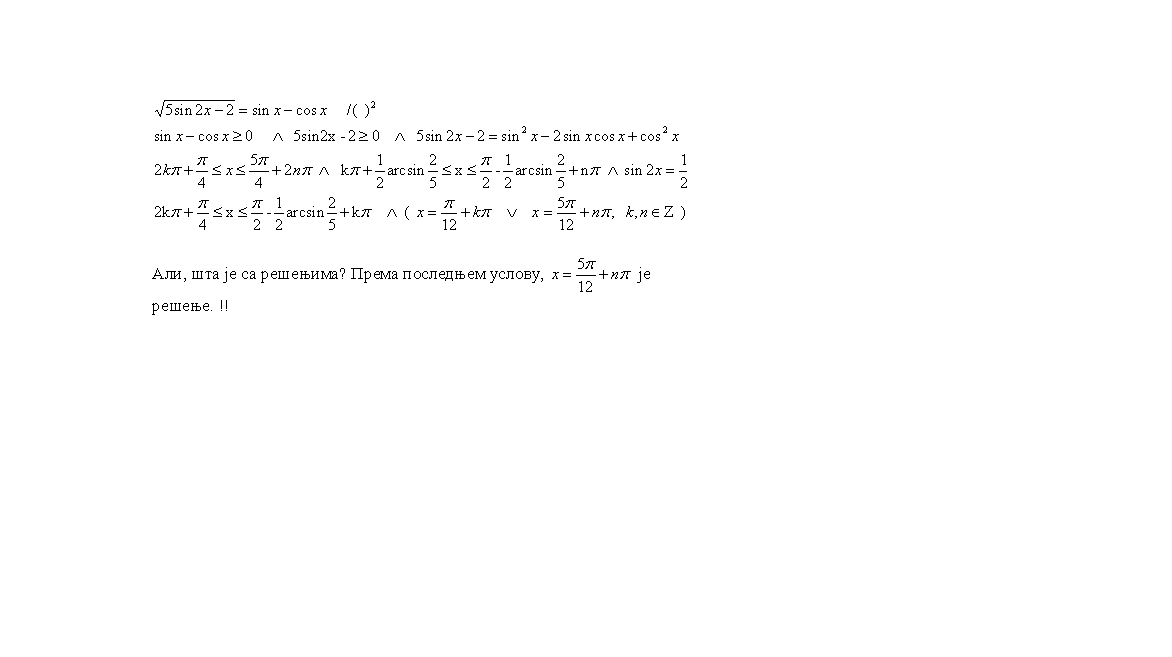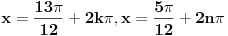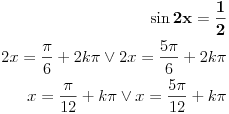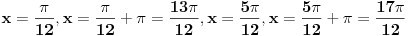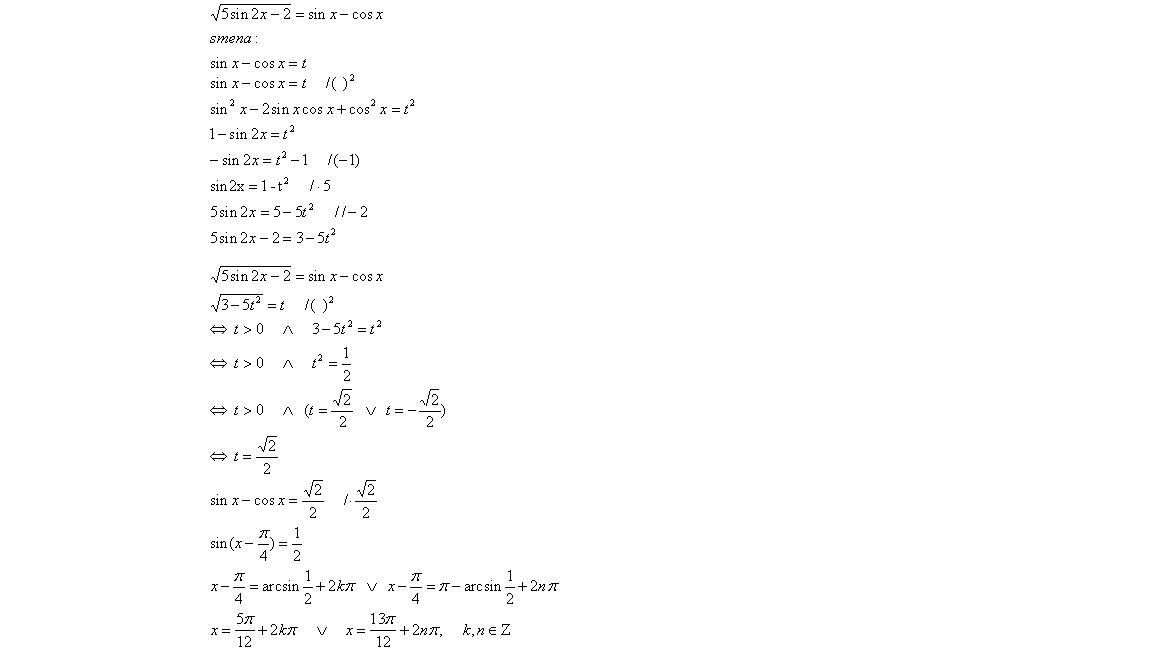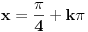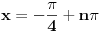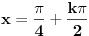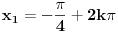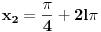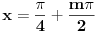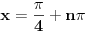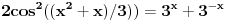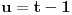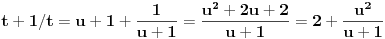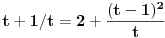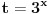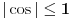|
|
[ kolev.biljana382 @ 08.03.2011. 21:16 ] @
|
| Molim Vas, treba mi hitna pomoc kako da resim sledece zadatke:
1. Izracunaj ctg(alfa - beta), ako je sin alfa = 1/4, a cos beta = 1/5. Ja sam pokusala preko formule za ctg (alfa - beta) = (ctg alfa ctg beta + 1) / ctg beta - ctg alfa, ali ne znam kako dalje. Molim nekog da mi resi.
2. Dokazati da je (1+ sin alfa - cos alfa) / (1 + sin alfa + cos alfa) = tg alfa / 2.
Ovaj nisam ni znala da pocnem. tg alfa pola je sin alfa / (1 + cos alfa) ili (1 - cos alfa) / sin alfa.
Hvala unapred. |
[ edisnp @ 08.03.2011. 22:59 ] @
1.)prvo trebas nacrtati trigonometrijski krug,zatim na  nadjemo vrednost 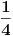 i povucemo pravu 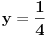 koja je paralelna sa 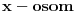 .Ta prava sece trigonometrijski krug u tackama  i  ,zatim te tacke spojis sa koordinatnim pocetkom i dobices trazene uglove.Sada slicno ide i za 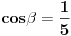 samo sto sada nalazis 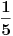 na 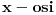 povuces pravu paralelnu sa pravom  one seku kruznicu u nekim tackama spojis te tacke sa koordinatnim pocetkom i dobijes uglove.I sad nastavis dalje. [ Nedeljko @ 08.03.2011. 23:27 ] @
1. Izrazi kotangens od alfa i beta preko datih sinusa i kosinusa, vodeći računa o znaku. Rekao bih da rešenje nije jednoznačno.
2. 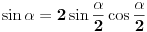 . U brojiocu još iskoristi vezu 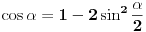 , a u imeniocu 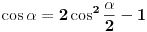 . [ atomant @ 08.03.2011. 23:52 ] @
Koristi vec dobro poznatu formulu 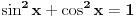 . Trebace ti trigonometrijski krug, jer recimo ako je 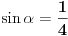 , onda 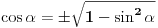 , jer je ovaj ugao smesten ili u prvom ili u drugom kvadrantu. Sada znas da je 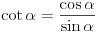 itd... Resenje nije jednoznacno, kao sto je Nedeljko vec rekao. [ devetkamp @ 21.11.2011. 13:36 ] @
Jel bi mi dao neko ideju kako da resim sledecu jednacinu? tgx + tg2x + tg3x = 0. Hvala unapred
[ darkosos @ 21.11.2011. 13:48 ] @
tgx + tg2x + tg3x = 0
Mozda moze ovako 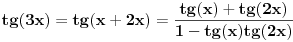
Pa mozes da izdvojis tg(x)+tg(2x) ispred zagrade:
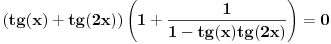 [ Sonec @ 21.11.2011. 20:18 ] @
A mozes i ovako:
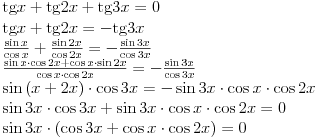
E sad, da vidimo sta cemo sa 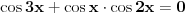 (kad posmatramo taj slucaj). Pa
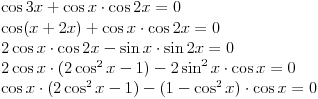
Uvedes smenu 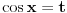 , pri cemu je 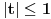 i resis po  , vratis itd, itd...
Posle ces lako naci resenja. [ devetkamp @ 22.11.2011. 17:39 ] @
Radio sam na onaj prvi nacin. Na kraju dobijem (tgx)^2= 1/2. I to resim. I jos, x = k*pi/3, kao resenje jednacine tgx + tg2x = 0. Probacu i ovaj drugi. Je li dobar rezultat?
[ Sonec @ 22.11.2011. 18:54 ] @
[ devetkamp @ 24.11.2011. 15:53 ] @
Ne ispada isto. Mada je moguce da su ta resenja napisana u drugom obliku....
[ Sherlock Holmes @ 24.11.2011. 17:27 ] @
Verovatno. Kada sam radio jednu trigonometrijsku jednačinu, otkucao je sam u Wolfram-u, dobio sam dosta složeno rešenje. Kada sam uspeo da rešim jednačinu, dobio sam kao u rešenjima, i rešenje je krajnje prosto. Dešava se.
[ devetkamp @ 06.01.2012. 08:27 ] @
Resavao sam jednacinu 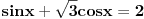 na dva nacina, i nisam dobio bas ista resenja. Prvi nacin svodi datu jednacinu na 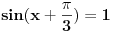 , a iz drugog dobijam 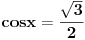 . Pitanje je jesu li resenja ovih jednacina ista? Hvala :D [ darkosos @ 06.01.2012. 08:55 ] @
[ Sherlock Holmes @ 06.01.2012. 10:01 ] @
[ devetkamp @ 06.01.2012. 10:08 ] @
U redu za uvodjenje pomocnog argumenta. Ali ja sam radio i metodu zamene, Pravio sistem sa osnovnim trigonometrijskim identitetom, i jednacinu sveo na 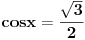 . Njena resenja su : 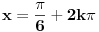 i 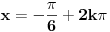 . Sta sa ovim drugim resenjem? Nisam bas najbolje razumeo [ darkosos @ 06.01.2012. 10:28 ] @
Posto ne vidim postupak, mogu samo da nagadjam da si uvodjenjem osnovnog trigonometrijskog identita ili mozda kvadriranjem negde izgubio znak, npr kao kad kvadriras x=1 i dobijes x^2=1 sto sad ima 2 resenja, 1 i -1.
[ devetkamp @ 06.01.2012. 10:51 ] @
sin x izrazim iz date jednacine i zamenim u identitetu. Dobijem kvadratnu jednacinu po cos x: 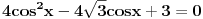 . Resenje je jedinstveno....
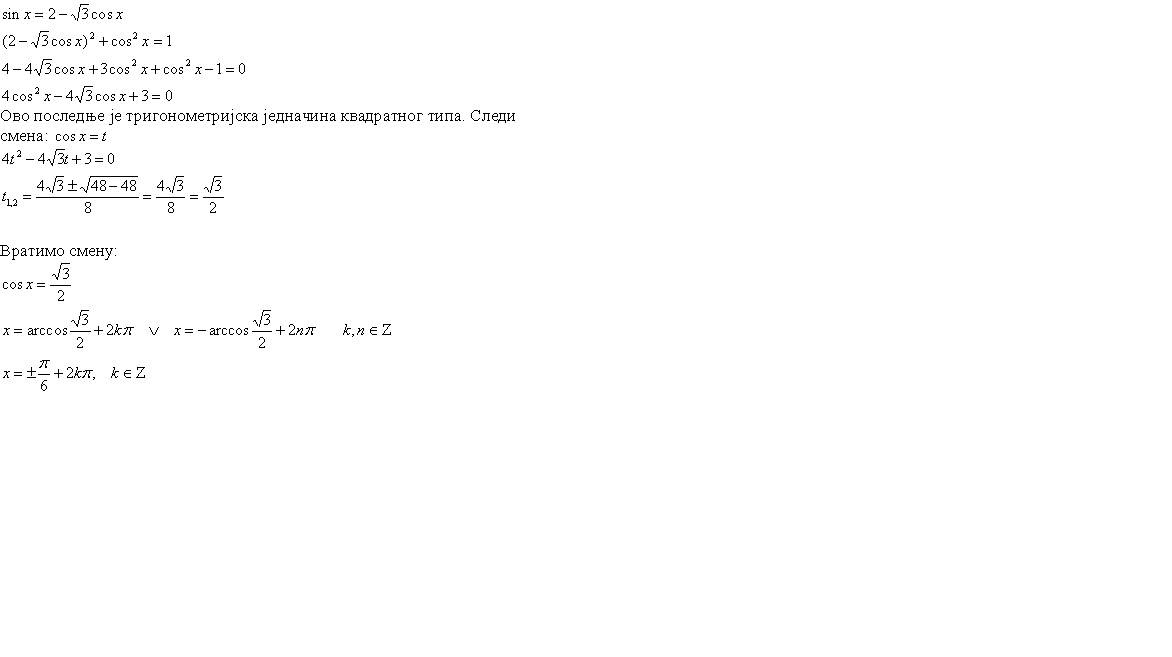 [ darkosos @ 06.01.2012. 11:13 ] @
Kada si izrazio iz linearne jednacine sin preko cos-a i zamenio u kvadratnu jednacinu, izgubio si znak te veze, dakle treba ti dodatni uslov;
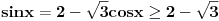 [ devetkamp @ 06.01.2012. 12:25 ] @
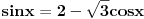 . Jel si mislio na to da ovaj desni izraz mora da bude izmedju -1 i 1? Pa se resi ta nejednacina? [ darkosos @ 06.01.2012. 12:34 ] @
Pa, u principu, osnovni identitet ne dozvoljava da vrednosti budu van inervala [-1,1] tako da nije to problem. Problem je u tome sto je
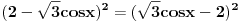 ali 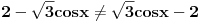 [ devetkamp @ 06.01.2012. 13:16 ] @
Resavanjem nejednacine 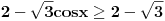 dobijam cosx manje ili jednako 1. ? [ darkosos @ 06.01.2012. 13:55 ] @
Ne bre :) imas uslov da je 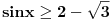 , sto ti onda "gasi" ona resenja gde to nije zadovoljeno. [ devetkamp @ 06.01.2012. 15:12 ] @
OK ! Radim maturski rad na temu trigonometrijske jednacine, pa pronalazim razne zadatke. Hvala!
[ devetkamp @ 07.01.2012. 20:05 ] @
Moze li neko samo da mi proveri resenja ove jednacine?
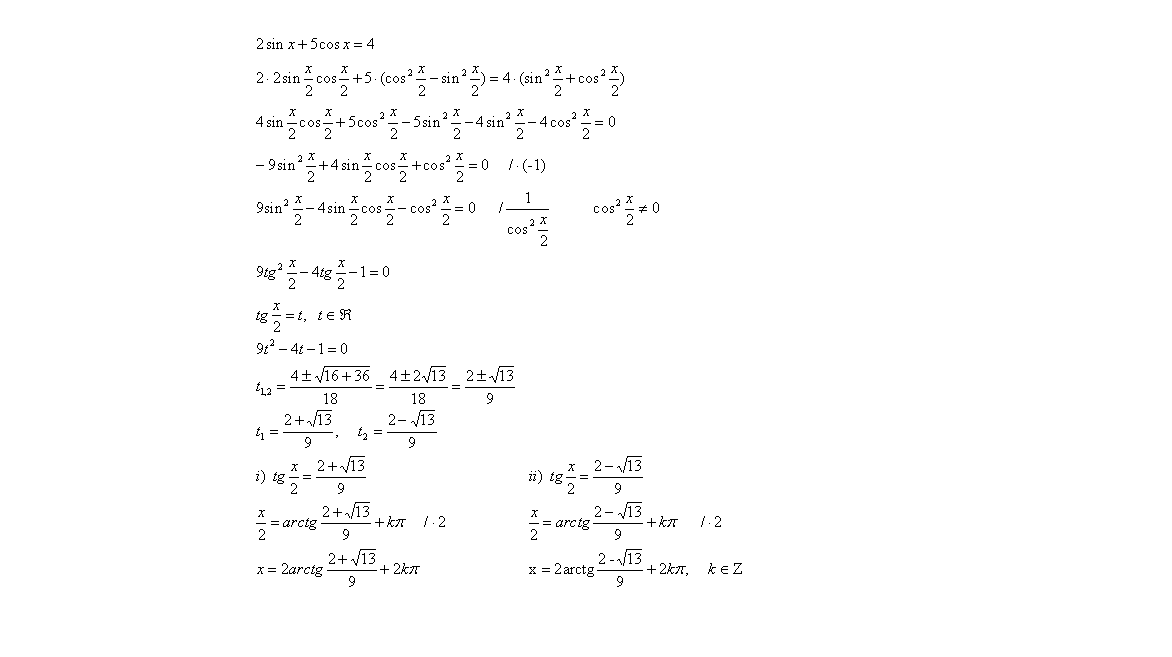 [ Sini82 @ 07.01.2012. 20:14 ] @
[ devetkamp @ 07.01.2012. 20:18 ] @
Radio sam i na drugi nacin, pa dobio malo drugacije...
 [ devetkamp @ 07.01.2012. 20:45 ] @
Mozda sam i spetljao nesto sa ovim uslovom....
[ Sini82 @ 07.01.2012. 21:03 ] @
Rješavao si jednačinu 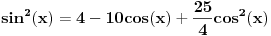 a ne početnu 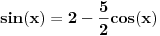 .
To bi bilo kao da si rješavao jednačinu 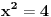 umjesto 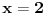 . Nije im isti skup rješenja.
Tako i kod prve dvije, imaš jednačine sa različitim skupovima rješenja (skup rješenja druge jednačine je podskup skupa rješenja prve):
http://www.wolframalpha.com/input/?i=1-cos^2(x)%3D4-10cos(x)%2B25/4cos^2(x)
http://www.wolframalpha.com/input/?i=sin(x)%3D2-5/2cos(x)
Moram da idem, nemam sada vremena da analiziram drugo rješenje koje si postavio. Da ne žurim rado bih ti pomogao. [ devetkamp @ 07.01.2012. 21:07 ] @
Hvala, i ovo je dovoljno
[ devetkamp @ 07.01.2012. 21:25 ] @
Evo kako su zadatak uradili u matematiranju. Ne vidim neku posebnu razliku u mom i njihovom resavanju...
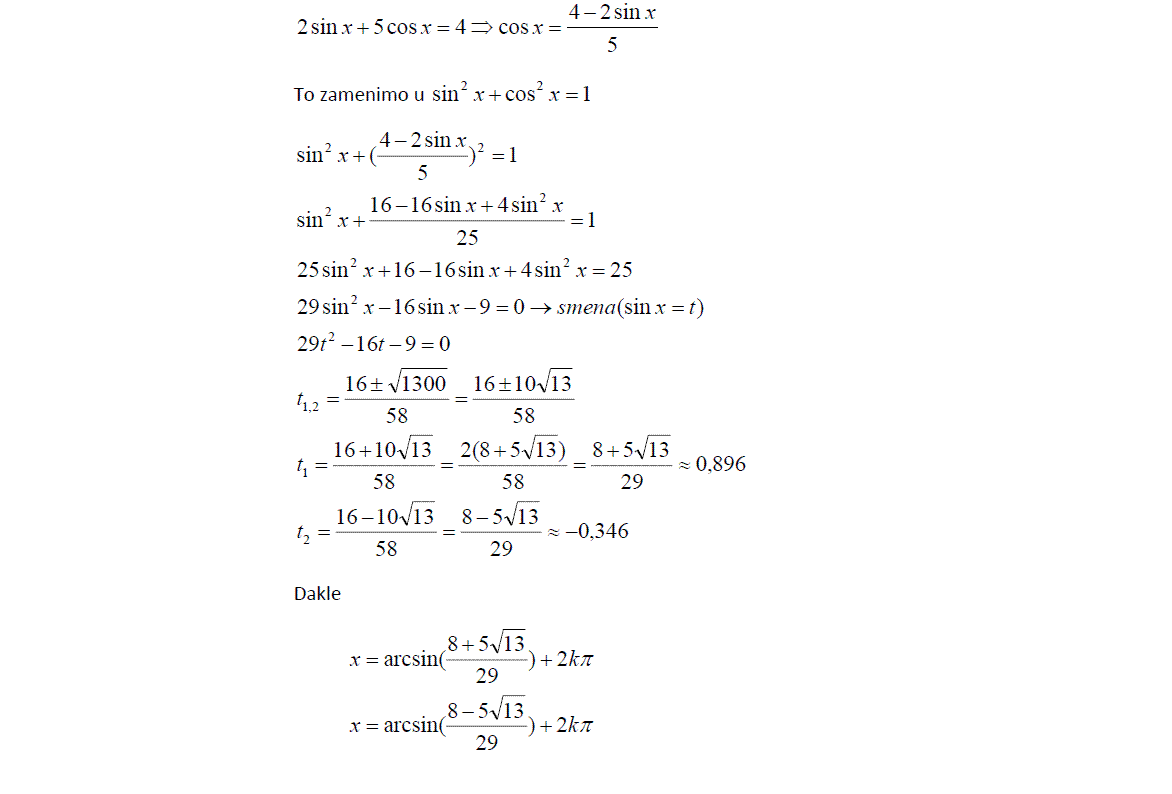 [ darkosos @ 08.01.2012. 00:20 ] @
Nisam jos 100% siguran je ovo sto sad pisem uvek tako, ali ocigledno da uslov na koji sam ti prethodno ukazao nije dovoljan; stvar se vrti negde oko toga da su uglovi za cos u kojima on ima istu vrednost takvi da sin u njima ima razlicit znak. Ova razlika se gubi u kvadratnoj jednacini ali naravno da je ima u linearnoj.
Takodje, uvek mozes proveriti resenja tako sto ces zameniti to u linearnu jednacinu i videti da li je ok. Ali probao sam da nadjem neke uslove koji bi odmah dali koja su resenja dobra a koja ne:
Iz 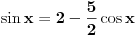 se moze zakljuciti da je 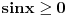 za 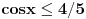 i 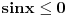 za 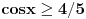
Sa ovim uslovima vidimo da za 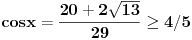 treba uzeti onaj ugao u kome je sin negativan, a to je 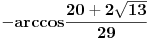 ,
dok za 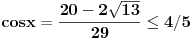 treba uzeti onaj ugao u kome je sin pozitivan, a to je 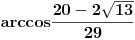 . [ devetkamp @ 08.01.2012. 09:18 ] @
Vidim da u ovom slucaju jeste tako. Bar kad su u pitanju sin i cos.
[ devetkamp @ 08.01.2012. 12:03 ] @
Ovo je tek muka :(
 [ Sherlock Holmes @ 08.01.2012. 12:18 ] @
Gde ti je uslov da je 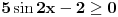 ? [ Sonec @ 08.01.2012. 12:21 ] @
@devetkamp: nisam siguran da si (za pocetak) dobro resio nejednacinu: 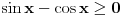 [ devetkamp @ 08.01.2012. 12:52 ] @
Evo kako sam resio nejednacinu...
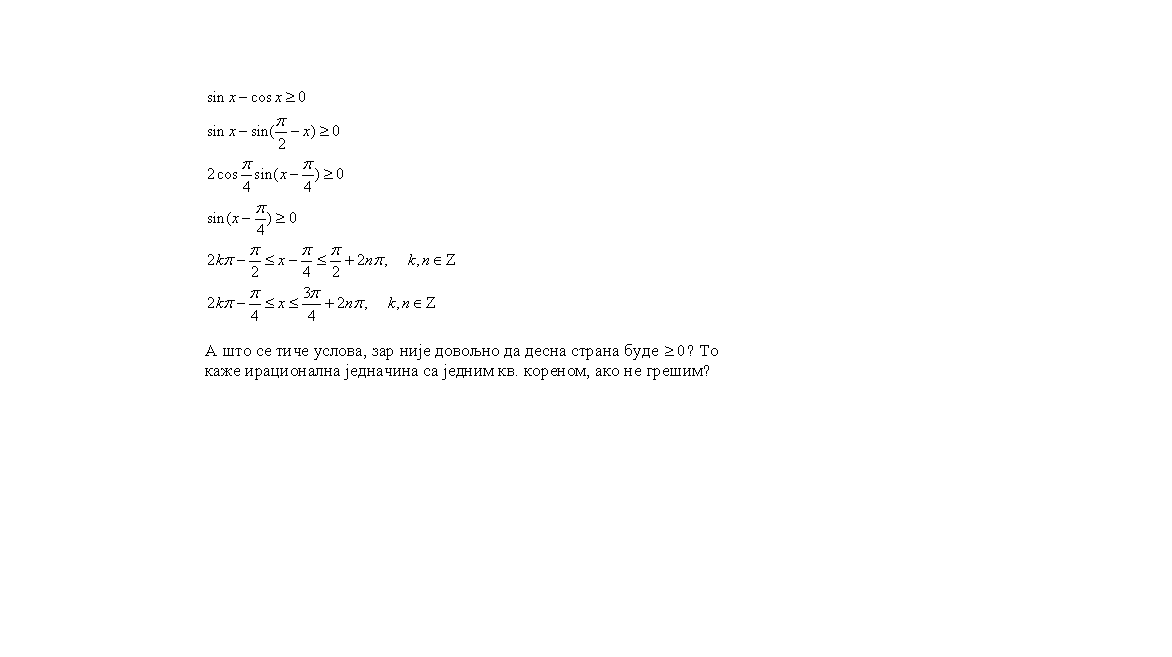 [ Sonec @ 08.01.2012. 13:05 ] @
Sinus je pozitivan na segmentu 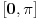 , a ne 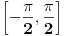 (plus period, tralala).
Iskreno, davno sam radio iracionalne jednacine, i prvo sam hteo da kazem da mora i potkorena velicina da bude veca ili jednaka od nule, a onda bacih pogled na matematiranje, i tamo pise kako si ti rekao, a u resavanju zadataka ONI dodaju i uslov za potkorenu velicinu.
Mislim da treba da se doda i taj uslov, jer inace nije definisan koren, a posto je koren pozitivna vrednost, onda imas onaj uslov za B itd, itd...
EDIT: i pogledaj ovde kako je clan @Farenhajt OVDE resio trigonometrijsku jednacinu (da, kod tebe je nejednacina, al se ponovo moze primeniti), a kasnije je Bojan resio malo tezi slucaj istom metodom. Ja sam tako ovde resio 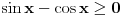 , nekako mi je lakse :)
[Ovu poruku je menjao Sonec dana 08.01.2012. u 14:46 GMT+1][ devetkamp @ 08.01.2012. 13:44 ] @
Dodao sam i taj uslov, i ispravio ono sto sam lupio za sin>0. I dobio ovako:
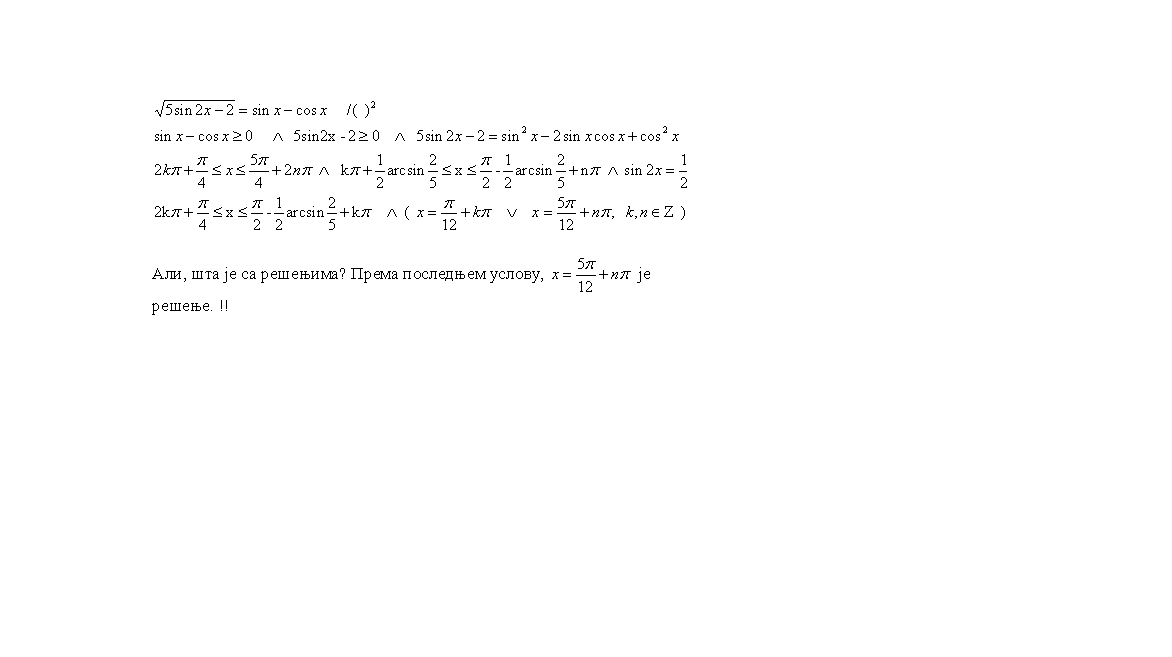 [ Sonec @ 08.01.2012. 14:00 ] @
[ devetkamp @ 08.01.2012. 14:23 ] @
U zbirci iz koje je zadatak resenje je 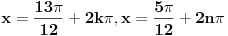 [ devetkamp @ 08.01.2012. 20:38 ] @
Kako da nadjem ovo drugo resenje?
[ Sonec @ 08.01.2012. 20:57 ] @
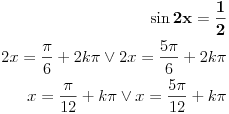
Ajmo, da bismo sveli na period 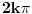 da vidimo koja su to resenja na segmentu 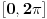 :
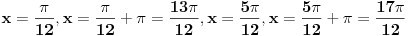
I onda proveris koja ti resenja pasuju, i na njih dodas sad period 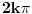 [ devetkamp @ 08.01.2012. 21:22 ] @
A zasto svodimo period na 2k pi ? Jel to znaci da dobijena resenja nisu tacna? Ili je to u vezi sa uslovima oko definisanosti korena polazne jednacine?
[ devetkamp @ 09.01.2012. 09:28 ] @
Uspeo sam da dobijem tacna resenja na sledeci nacin. Nadam se da je ispravan:
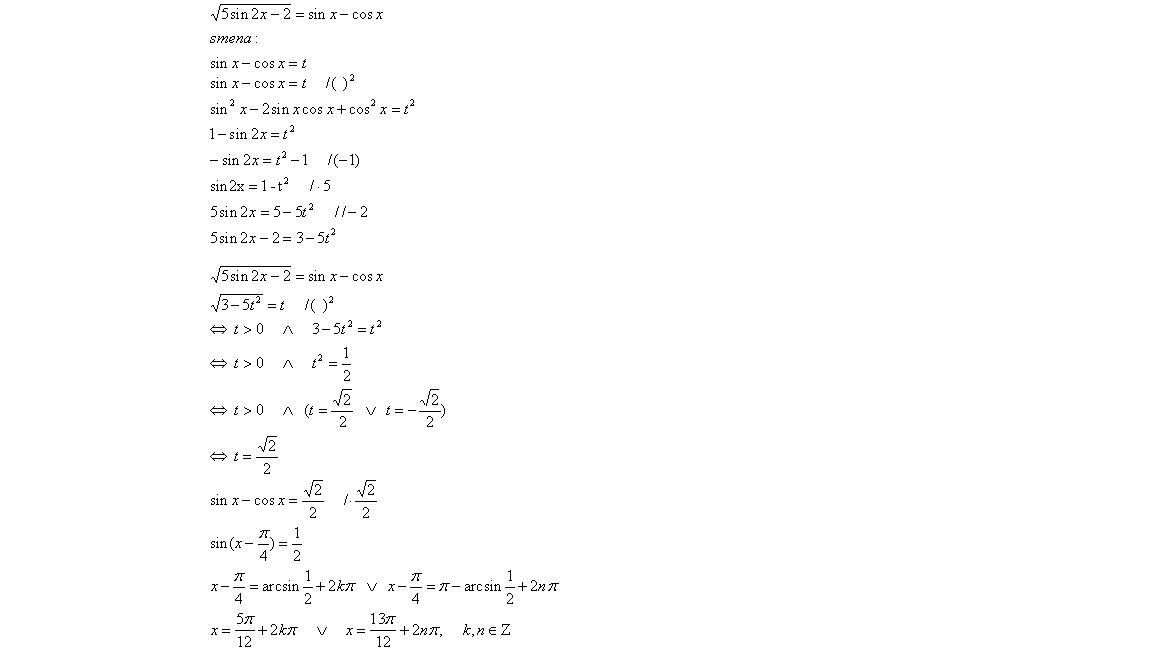 [ darkosos @ 09.01.2012. 10:38 ] @
Generalno govoreci (nisam previse ulazio u resenja koja si dao), od nacina resavanja ne sme da zavisi tacnost resenja. Hocu da kazem, kakav god metod izabrao, ako radis ispravno, moras dobiti tacna resenja.
Naravno, moze postojati primereniji (ili jednostavniji) metod za neku klasu jednacina/nejednacina.
Dakle, kako bi ti sad odlucio kojom metodom da krenes, ovom poslednjom ili onom prethodnom? Kako ces biti siguran da je resenje koje si dobio dobro? Ako ispravno radis, imas jedan niz implikacija,
koji ti garantuje da se sva resenja polazne jednacine nalaze u skupu koji si dobio na kraju. Ali koja od njih si dobra? Pa, generalno, to se vidi zamenom resenja u polaznu jednacinu, sto nekad moze da bude komplikovano.
Drugi nacin da odvojis zito od kukolja je da postavljas uslove pri kojima nesto vazi, tako da umesto implikacija dobijas niz ekvivalencija, i onda to garantuje tacnost svih dobijenih resenja.
Sto se tice prethodnog resenja, moguce je da je i ono dobro, ali nije tako jednostavno dobiti koja od resenja zadovoljavaju postavljene uslove. Zato ti je Sonec rekao da ih svedes na 2kpi, jer se tako lakse uporedjuju.
Doduse, imas tu taj neprijatan arcsin(2/5), pa to jos dodatno otezava poredjenje. Ali ako to uradis na ispravan nacin, sigurno dobijas tacno resenje.
[ devetkamp @ 09.01.2012. 13:47 ] @
Ok, hvala na vrlo korisnom savetu. Doduse, potrebno mi je vise matematickog iskustva, da bih i sam osetio strogost matematickog zakljucivanja. Krenem da resavam na jedan nacin, vidim da ne ispada kako treba i odmah trazim drugi... Slazem se da je to pogresno.
[ devetkamp @ 10.01.2012. 21:22 ] @
Imam jos jedno pitanje: Kako je najlakse sklopiti zajednicko resenje za neku trigonometrijsku jednacinu. Npr 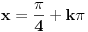 i 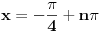 se spaja u 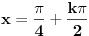 ? Moze li to bez ispisivanja resenja jednog, pa drugog skupa i nalazenja veze izmedju njih? Hvala. [ darkosos @ 11.01.2012. 09:17 ] @
Pa jedino sto mi pada na pamet jeste da vidis da li je jedna klasa resenja u aritmetickoj sredini druge:
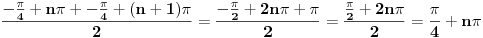 [ devetkamp @ 11.01.2012. 09:41 ] @
To je nesto sto me jako buni, jer se u resenjima mnogih zbirki nalazi samo zajednicko resenje. I prva pomisao: greska. Ono naravno, nije greska ako ostavimo resenja tako. Negde sam procitao da ukoliko dobijemo dva resenja (kao u primeru koji sam naveo), i ako oni u trigonometrijskom krugu obrazuju 180 stepeni, u zajednickom resenju se pise period kpi. E sad, ostaje da nagadjam, ako (kao u mom primeru) obrazuju 90 stepeni, period je kpi/2.
[ Sonec @ 11.01.2012. 09:55 ] @
Pa ne mora da vazi, recimo da si imao 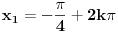 i 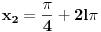 njihovo zajednicko resenje nije 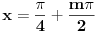 , nije ni 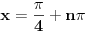
Al mozda ako ona (resenja) obrazuju ugao koji je polovina perioda i jednog i drugog resenja, onda mozemo da smanjimo period tako sto cemo da ga podelimo sa 2 (i dodamo ugao od jednog resenja).
Mozda je tu caka, a mozda i nije. Al mislim, uvek mozes da nacrtas malo vise resenja, i jedna i druga, i onda da uocis neku pravilnost (ukoliko ona postoji). [ darkosos @ 11.01.2012. 09:57 ] @
Nije bas nagadjanje, ako su resenja oblika 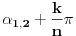 onda je jedini nacin da ih "skupis" da, kao u proslom primeru, oni predstavljaju uglove cija je razlika konstantna, i naravno jednaka 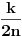
A sto se tice perioda, pa pi/2 radijana ti je zapravo 90 stepeni :) [ devetkamp @ 13.05.2012. 13:07 ] @
Jel moze predlog kako da resim sledecu jednacinu: 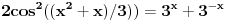 . Vidi se da je resenje 0. Ali kako doci do toga? [ Nedeljko @ 13.05.2012. 13:48 ] @
Pa, funkcija 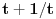 za 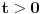 dostiže minimum u tački 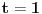 . Zaista, za 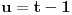 je
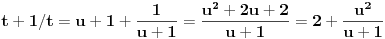
ili
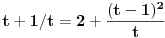 .
Dakle, za 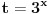 se dobija da je desna strana jednakosti uvek veća od 2, osim u tački 0 gde je vrednost jednaka 2, a leva strana jednakosti je uvek manja ili jednaka od 2 (zbog 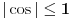 ). Stoga je jedino eventualno rešenje  za šta se neposrednom proverom utvrđuje da jeste rešenje.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|