prvi korak proveravas da li vazi za
i dobije dakle nejednakost je zadovoljena.Drugi korak za
dobijamo indukcijska pretpostavka koja je uvek tacna.Treci
korak dokazujemo da nejednakost vazi i za i dobijamo
dalje dobijas sada izvuces polaznu nejednakost
i dobijas sada je ostalo dokazati ona
se dokazuje na isti nacin dakle ponavljas isti postupak dok ne dokazes ili dok ne dobije ociglednu nejednakost koja je tacna.

Hvala na odgovoru, samo ne razumem onaj deo sa izvlacenjem pocetne nejednakosti.

Dakle treba da dokazemo da nejednakost vazi za neko i dobili smo
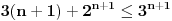
sto je ekvivalento sa
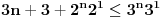
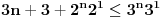
i sad u ovoj nejednakosti treba da uocimo prvu nejednakost
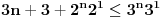
kad sredimo ovu nejednakost dobijemo
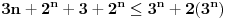
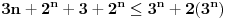
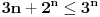
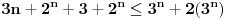
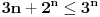
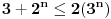
sad mi u ovoj nejednakosti prepoznajemo indukcijsku pretpostavku koja je uvek tacna dakle prepoznaje ovu nejednakost i sad ako od ove oduzmemo ovu nejednakost ostalo nam je to je dakle ta nejednakost koja treba da se dokaze znaci izvukli smo indukcijsku pretpostavku.Mozda sam sad malo preterao nadam se da vas nisam zbunio.Dakle kod ovakvih zadataka je fora izvuci indukcijsku pretpostavku i onda dokazivati taj ostatak sto je ostao nakon sto smo izvukli indukcijsku pretpostavku.

Verovatno sam dosadan, ali ne razumem kako iz ovog smo dobili ovo

Pa kako mozes da napises mozes kao to bi bilo
isto kao kad bi napisao a to je jednako
a mozes da pises kao sto je jednako
isti primer kako mozes da napises to mozes da predstavis kao ili kao .
Dakle ovo je jednako ovome samo sto smo jedne te istu nejednakost zapisali u dva razlicita oblika.Nadam se da je sad jasno.

Ovako:

I još treba na kraju dokazati da vrijedi ona poslednja nejednakost:
Dodaj na obe strane 3n pa oduzmi početni uslov.Dobićeš da je 3 manje ili jednako od...

Poslednja nejednakost sledi iz induktivne pretpostavke.