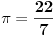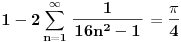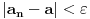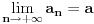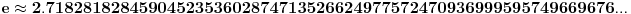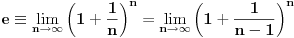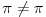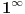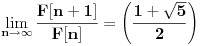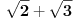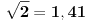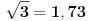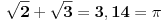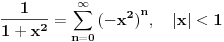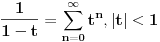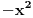[ edisnp @ 26.03.2011. 20:41 ] @
|
[ del-boy @ 26.03.2011. 20:58 ] @
Grešiš. Pi je samo približno jednak 22/7, ako se dobro sećam poklamanje je do treće ili četvrte decimale. Korisno je za brze proračune kad preciznost nije mnogo bitna...
[ SrdjanR271 @ 27.03.2011. 15:28 ] @
22/7=3.14285..... dok je Pi=3,1415926.... znači tacne su samo 2 decimale.
Pored toga sto je transcedentan on je i iracionalan (dokazano) tako da sigurno nije neki razlomak. Broj pi se racuna preko redova najefikasnije (može i preko beskonačnih proizvoda). http://mathworld.wolfram.com/PiFormulas.html Evo jedna lepa aproksimacija gde ima i 22 a poklapa se 8 decimala. 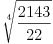 [Ovu poruku je menjao SrdjanR271 dana 27.03.2011. u 18:12 GMT+1] [ SrdjanR271 @ 27.03.2011. 19:32 ] @
Sta znaci "transcendentan"?
[ atomant @ 27.03.2011. 20:34 ] @
[ igorpet @ 27.03.2011. 20:38 ] @
Citat: Gost: Sta znaci "transcendentan"? Citat: Pi je iracionalan broj, što znači da se njegova vrednost ne može izraziti preko razlomaka. Zbog toga njegov decimalni zapis nema kraja i nije periodičan. Pi je takođe transcendentan broj, što znači da ga nije moguće izraziti korišćenjem konačnog broja celih brojeva uz četiri osnovne računske operacije (sabiranje, oduzimanje, množenje i deljenje) i korenovanja. [ Nedeljko @ 27.03.2011. 21:09 ] @
Ne, to nije definicija transcedentnog broja. Transcedentan broj je onaj koji nije algebarski, to jest, nije koren nijednog nekonstantnog polinoma sa celim (odnosno racionalnim) koeficijentima.
Rešenja algebarskih jednačina do četvrtog stepena se zaista mogu izraziti preko koeficijenata jednačine, celih brojeva, operacija sabiranja, oduzimanja, množenja, delenja i korenovanja proizvoljnog stepena, ali kod jednačina petog i višeg stepena to uopštem slučaju nije slučaj. [ Nedeljko @ 28.03.2011. 19:47 ] @
Ako gledamo decimalni zapis broja PI onda je taj zapis sve tačniji sa povećanjem broja cifara, ali se iz tih
zapisa ne može zaključiti kako tako upisane vrednosti konvergiraju prema graničnoj vrednosti. Ili grešim? [ miki069 @ 28.03.2011. 22:45 ] @
Šta znači "tačniji" zapis?
[ SrdjanR271 @ 28.03.2011. 22:51 ] @
Tacno je da je sa povećanjem broja decimala (tačnih) i broj pi tačniji.
Ali gledanjem u decimale možeš samo da gledaš. pogledajmo ovo: 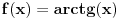 Prvi izvod od f je 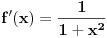 sada se f' može predstaviti stepenim redom 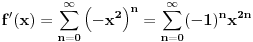 Za 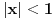 Sada se treba vratiti iz f' u f 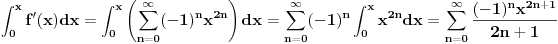 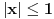 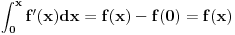 Konačno 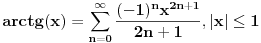 Neko se setio da je arctg(1)=Pi/4 :) 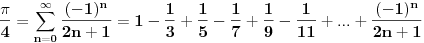 Ali ovo užasno sporo konvergira ka Pi pa je ovakvo računanje broja Pi totalno neefikasno. Mnogi su pravili modifikacije ovog reda (poznat kao Gregori-Lajbnicov), Gauss, Ojler, Machin... John Machin je "našao" sledeću vezu (može se izvesti korišćenjem f-le 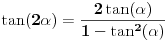 ) )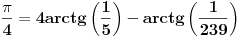 Odnosno 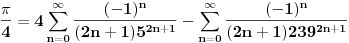 Suma prvih 10 članova ovih gore redova daje Pi sa 16 tačnih decimala što je jako brzo. 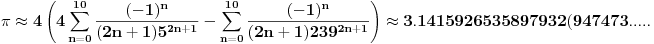 Za prvih sto članova greska je 9x10^(-144) [Ovu poruku je menjao SrdjanR271 dana 29.03.2011. u 02:39 GMT+1] [ Nedeljko @ 29.03.2011. 08:47 ] @
Citat: Gost: Ako gledamo decimalni zapis broja PI onda je taj zapis sve tačniji sa povećanjem broja cifara, ali se iz tih zapisa ne može zaključiti kako tako upisane vrednosti konvergiraju prema graničnoj vrednosti. Ili grešim? Šta to znači "kako konvergiraju"? Znam za dve osnovne vrste konvergencije brojnih redova - običnu i apsolutnu, kao i za još neke opštije izvedene iz Teplicove teoreme. Na šta si zapravo mislio? [ Nedeljko @ 29.03.2011. 09:21 ] @
Citat: Nedeljko... Na šta si zapravo mislio? Mislio sam na zakonitost konvergencije ako uzmeš nekoliko uzastopnih vrednosti u decimalnom zapisu. [ Nedeljko @ 29.03.2011. 12:17 ] @
Misliš na brzinu konvergencije, tj. procenu ostatka? Da, to se ne utvrđuje posmatranjem prvih nekoliko članova niza, ali se može izračunati na osnovu opšteg člana.
Evo, recimo, za 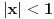 je je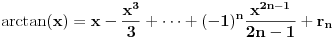 , gde je , gde je 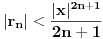 . .To je posledica činjenice da članovi razvoja arkustangensa naizmenično menjaju znak i da je po apsolutnoj vrednosti svaki sledeći manji od prethodnog. [ SrdjanR271 @ 29.03.2011. 18:04 ] @
@Gost
Misliš kao što je 1/7=0.14285714285714285714.... pa se "ekipa" 142857 ponavlja, da i u Pi ima neka logika ponavljanja neki "patern"? Da li je to "konvergencija decimala"? Ako jeste onda Pi nije "konvergentan u tvom smislu". :) Jer je Pi iracionalan. [ SrdjanR271 @ 29.03.2011. 19:33 ] @
Citat: Ne mislim da je tako jer znam da Pi nije razlomak nego, na primer, ovako: Pi/4 = 1 - 2(1/(3x5) + 1/(7x9) + 1/(11x13) + ...) [ Nedeljko @ 30.03.2011. 06:43 ] @
@Gost
Hteo si da pitaš da li neki red konvergiira ka pi? Pa, to se dokazuje. Ne može na osnovu prvih nekoliko članova. [ Nedeljko @ 30.03.2011. 09:53 ] @
Citat: Nisam. To je bio samo odgovor Srdjanu. Ustvari pitao sam kako neki niz u decimalnom zapisu konvergira ka pi. Čudna a i jako interesantna stvar je u tome što sa brojevima u decimalnom zapisu na brojnoj pravoj nikako ne mozemo "pogoditi" to mesto gde se nalazi broj pi. [ Nedeljko @ 30.03.2011. 10:55 ] @
Sad mi uopšte više nije jasno šta si hteo da pitaš.
Šta ti je pre svega broj u decimalnom zapisu? Je li to broj sa konačnim dekadnim zapisom ili dozvoljavaš i beskonačne? Broj pi, kao i svaki realan broj ima dekadni zapis (koji je u slučaju broja pi beskonačan). Drugo, da li znaš definiciju konvergencije? [ Nedeljko @ 30.03.2011. 10:57 ] @
Uzgred, do sada je izračunato 5,000,000,000,000 (5x1012) cifara broja pi. To je trenutni svetski rekord.
[ edisnp @ 30.03.2011. 10:59 ] @
Mene interesuje definica konvergencije?
[ edisnp @ 30.03.2011. 11:56 ] @
Mogu da prepričam - ako se u proizvoljno maloj okolini granične vrednosti nalaze gotovo svi članovi nekog niza
[ Nedeljko @ 30.03.2011. 14:52 ] @
[ Nedeljko @ 30.03.2011. 20:05 ] @
Citat: Nedeljko: Uzgred, do sada je izračunato 5,000,000,000,000 (5x1012) cifara broja pi. To je trenutni svetski rekord. Mi ustvari ne znamo koliki je broj pi. [ Nedeljko @ 30.03.2011. 21:00 ] @
Šta ti sad to znači "koliki je"? Pozicioni sistemi nisu jedini način predstavljanja brojeva. Redovi, limesi i integrali su isto toliko egzaktan način definisanja realnih konstanti.
[ Nedeljko @ 30.03.2011. 22:16 ] @
Citat: Nedeljko: Šta ti sad to znači "koliki je"? Pa to što piše! To je isto kao kad bismo pitali šta pretstavlja reč "znači". Pretpostavlja se poznavanje srpskog jezika. Citat: Redovi, limesi i integrali su isto toliko egzaktan način definisanja realnih konstanti. Da, ali za neke konstante znamo kolike su a za neke ne znamo. [ Nedeljko @ 30.03.2011. 22:42 ] @
Dobro, koliki je broj 2? Kolika je imaginarna jedinica? Koliki je broj -5? Koliki je broj 3/7? Koliki je broj -7/13?
[ edisnp @ 30.03.2011. 23:53 ] @
Ih sad ovo postaje malo ironicno.
[ edisnp @ 31.03.2011. 07:45 ] @
Jedinica je mera za brojeve. Broj je toliki koliko sadrži jedinica i (ili) njenih jednakih delova.
[ Nedeljko @ 31.03.2011. 13:02 ] @
Mogu li ja da znam kolika je širina mog prozora, obzirom da je apsolutno tačno merenje nemoguće (a i prozor se na mikronivou stalno menja)? Koje se fizičke veličine znaju?
[ Nedeljko @ 31.03.2011. 18:20 ] @
Približne.
[ Nedeljko @ 31.03.2011. 21:15 ] @
Pa i vrednost broja pi je u dekadnom sistemu zapisana približno i to sa mnogo većom tačnošću od bilo koje fizičke veličine.
[ Nedeljko @ 31.03.2011. 21:28 ] @
Veća ili manja netačnost je uvek netačnost
[ Nedeljko @ 31.03.2011. 21:44 ] @
OK, znači nijedna fizička veličina se ne zna.
Po tvojoj formulaciji "zna se koliki je neki broj" ako i samo ako je dokazano da je racionalan i znaju mu se brojilac i imenilac. Ja to do sada zaista nigde nisam sreo. [ Nedeljko @ 01.04.2011. 07:26 ] @
Broj pi nije jednak 3, ali on nije jednak ni vrednosti iskazanoj sa bilo koliko decimala. Možemo sužavati granice intervala u kom se nalazi
broj pi koliko god hoćemo, ali isto tako možemo samo da kažemo "tu je negde" jer u tom intervalu ma kako bio mali nalazi se i beskonačno mnogo drugih brojeva. [ Nedeljko @ 01.04.2011. 12:23 ] @
I koja je onda razlika u odnosu na fizičke veličine? Rekao bih da imaš duple aršine.
[ Nedeljko @ 01.04.2011. 14:05 ] @
Ja bih rekao da si negde pogrešio. Ta razlika potencirana je samo na jednom mestu:
Citat: Nedeljko: Pa i vrednost broja pi je u dekadnom sistemu zapisana približno i to sa mnogo većom tačnošću od bilo koje fizičke veličine. [ Nedeljko @ 01.04.2011. 15:06 ] @
@Gost
Čekaj, tvrdiš da se ne zna koliki je pi, a da se zna kolike su fizičke veličine. O čemu ti to? [ Nedeljko @ 01.04.2011. 15:26 ] @
Citat: Napravi niz pa da Nedeljko kaže da li pi pripada tom nizu ili ne. Citat: Nedeljko: Čekaj, tvrdiš da se ne zna koliki je pi, a da se zna kolike su fizičke veličine. O čemu ti to? Ko je rekao da se zna kolike su fizičke veličine? [ Nedeljko @ 01.04.2011. 16:42 ] @
Aha, znači, ni one se ne znaju.
Vidiš, za broj  postoji algoritam, koji za dato prirodno n nalazi racionalne brojeve a i be, takve da je postoji algoritam, koji za dato prirodno n nalazi racionalne brojeve a i be, takve da je 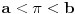 i i 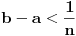 , odnosno postoji algoritam koji za dato n daje n-tu decimalu broja , odnosno postoji algoritam koji za dato n daje n-tu decimalu broja  . Takvi algoritmi nose punu informaciju o broju . Takvi algoritmi nose punu informaciju o broju  . E, sad, ti preferiraš razlomke. To je stvar tvog ukusa, a ne neki fundamentalni gnoseološki razlog da jedan od ta dva zapisa smatraš rešenim oblikom, a drugi ne. . E, sad, ti preferiraš razlomke. To je stvar tvog ukusa, a ne neki fundamentalni gnoseološki razlog da jedan od ta dva zapisa smatraš rešenim oblikom, a drugi ne.[ Nedeljko @ 01.04.2011. 16:43 ] @
E, da, pozvao si s i na Srpski jezik. U kom si rečniku pročitao tu formulaciju znanja kolika je neka konstanta?
[ Nedeljko @ 01.04.2011. 17:54 ] @
Citat: Nedeljko: Takvi algoritmi nose punu informaciju o broju  . . Dažbe! Iz te puške nikad nećeš pogoditi broj  već nedužne brojeve u njegovoj okolini koji mu nisu ni slični. već nedužne brojeve u njegovoj okolini koji mu nisu ni slični.Rečnike retko čitam. To je prilično nezanimljiva literatura. [ Nedeljko @ 01.04.2011. 18:29 ] @
O tome što ne razumneš šta je puna informacija o nečemu nema svrhe da raspravljam sa tobom, jer to jednostavno ne možeš da shvatiš.
Što se tiče ovog drugog, bitno je da se pozivaš na nešto što ne čitaš. [ SrdjanR271 @ 01.04.2011. 19:04 ] @
Citat: Gost: Dažbe! Iz te puške nikad nećeš pogoditi broj  već nedužne brojeve u njegovoj okolini koji mu nisu ni slični. već nedužne brojeve u njegovoj okolini koji mu nisu ni slični.Rečnike retko čitam. Slažem se donekle sa ovim, ali me muči nešto drugo. Da li ti možeš iz svoje puške da pogodiš Pi ili šta je poenta? [ SrdjanR271 @ 01.04.2011. 20:17 ] @
Citat: Nedeljko: O tome što ne razumneš šta je puna informacija o nečemu nema svrhe da raspravljam sa tobom, jer to jednostavno ne možeš da shvatiš. Problem je, dakle, u mom nivou shvatanja. Dobro. Ali ako ja ne mogu da dosegnem tvoj nivo shvatanja ti lako možeš da se spustiš na moj. Pomoću tog algoritma može se formirati niz približnih vrednost broja  . Svaki član toga niza ima konačan broj decimala pa prema tome . Svaki član toga niza ima konačan broj decimala pa prema tome broj  ne pripada tom nizu. ne pripada tom nizu.[ igorpet @ 01.04.2011. 20:18 ] @
Interesantna tema a postovi jos interesantniji.
Deluje ko da ovde svi govorimo istim jezikom, a ipak nikako da se razumemo Bas me interesuje da li ce pi do kraja biti pogodjen nekom puskom! Nego, interesuje me koju mu decimalu gadjate? [ igorpet @ 01.04.2011. 20:22 ] @
Citat: SrdjanR271: Da li ti možeš iz svoje puške da pogodiš Pi ili šta je poenta? Nema takve puške. [ SrdjanR271 @ 01.04.2011. 20:39 ] @
Znam da nema, zato i pitam. Šta je onda poenta tvoje priče?
[ Nedeljko @ 01.04.2011. 21:01 ] @
Citat: Gost: Pomoću tog algoritma može se formirati niz približnih vrednost broja  . Svaki član toga niza ima konačan broj decimala pa prema tome broj . Svaki član toga niza ima konačan broj decimala pa prema tome broj  ne pripada tom nizu. ne pripada tom nizu.Algoritam je konačan matematički objekat. Ne moraš ga pokretati uopšte. On već sadrži informaciju o svim decimalama broja pi. Taj algoritam je jedna vrsta zapisa broja pi. Ne moraš ga uopšte pretvarati u druge zapise. Ti si se uhvatio za racionalne brojeve samo zato što ih voliš, a ne iz nekog fundamentalnog razloga. Po čemu se "zna" koliko je 3/7, a "ne zna" koliko je [tex]\sqrt 2[tex]? [ petarm @ 01.04.2011. 21:57 ] @
Mislim da je filozofija člana zvanog Gost da ako imam neki krug precnika npr.
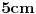 po njemu ti čak i ako imaš algoritam za računanje svake cifre broja po njemu ti čak i ako imaš algoritam za računanje svake cifre broja  nećeš moći da ih uračunaš u obim. Ali Gostu možeš napisati nećeš moći da ih uračunaš u obim. Ali Gostu možeš napisati 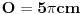 i gotova priča. E sad priča oko merenja. Fizika nije egzaktna nauka zato što fizičar nešto meri tačno. Ne meri on tačno ništa. Egzaktna je iz razloga što se zna sa kojom je greškom nešto izmereno. [ kandorus @ 01.04.2011. 23:27 ] @
^Gost: "ako ja ne mogu da dosegnem tvoj nivo shvatanja ti lako možeš da se spustiš na moj."
Može da bude ali ne mora da znači. Na primer, uspostavljanje bijekcije izmedju skupova rešavanog problema i skupova nekog već rešenog problema je dosta zgodan metod rešavanja zadataka. Problem nastaje ako to pokušavaš da objasniš diplomiranom inženjeru elektrotehnike. Posebno ako ti on da zadatak za n=3 a ti rešiš za proizvoljno n, jer kakvo je to rešenje ako nije rešeno za bilo koje n? Taj inženjer će takvo objašnjenje da shvati kao zahebavanje sa "bijekcijom" a ti ne umeš rešenje da prilagodiš i objasnš da te svaki razume. Zato to "lako" može da bude itekako teško i nekad je lakše ono što "ne mogu". [ kandorus @ 02.04.2011. 08:06 ] @
Citat: Nedeljko: Algoritam je konačan matematički objekat. Ne moraš ga pokretati uopšte. On već sadrži informaciju o svim decimalama broja pi. Taj algoritam je jedna vrsta zapisa broja pi. Ne moraš ga uopšte pretvarati u druge zapise. Koliko se ja razumem u tu drvenariju decimale su racionalni brojevi - dakle algoritam sadrži informacije o "svim decimalama" broja pi odnosno o svim racionalnim delovima broja pi. I ko sad više voli racionalne brojeve? Ako uzmeš bilo koju sumu od n decimala onda je ta suma racionalan broj i sad ako skoknemo do beskonačnosti onda se ta suma pretvorila u transcendentan broj što ne može biti jer broj koji je suma decimala, odnosno suma racionalnih brojeva, nije transcendetan. Drugim rečima ti tvrdiš da transcendentni brojevi ne postoje. Ako od transcendentnog broja oduzmeš racionalan broj ostatak je uvek transcendentan, a pošto broj pi nije član niza približnih (racionalnih) vrednosti vrednosti broja pi onda uvek ostaje transcendentni ostatak koji nikako i nikad ne može biti "pojeden" racionalnim decimalama. Ako bi broj pi bio suma racionalnih brojeva on bi bio racionalan čak i ako ta suma ima beskonačno mnogo racionalnih sabiraka. [ kandorus @ 02.04.2011. 10:32 ] @
Na prvoj strani ove teme ti je SrdjanR271 dao formulu u kojoj je svaki član racionalan broj a njihova suma je ipak transcedentan broj.
Što se tiče algoritma, zavisi od koje definicije podješ. Ako je uslov da se procedura završi u konačnom broju koraka onda nema algoritma koji izračunava vrednost transcedentnog broja. Ali ako se taj uslov oslabi i zahteva samo da je procedura dobro definisana onda postoji algoritam koji izračunava Pi samo što se nikad ne završava. Sa postojanjem i nepostojanjem brojeva se može široko razgovarati. Teško je zamisliti da postoji bilo šta osim prirodnih brojeva. Realni brojevi su više "nerealni" nego "realni" jer ne možeš nikako izračunati taj broj Pi (u konačnom broju koraka) iako je "realan". Ali, postoji prirodan odnos kružnice i prečnika vezanih brojem Pi, dakle Pi je "realan". No, sve to nije bitno jer u matematici je bitno jedino ono što je dogovoreno kao definicija. [ Nedeljko @ 02.04.2011. 10:37 ] @
Citat: Gost: Ako bi broj pi bio suma racionalnih brojeva on bi bio racionalan čak i ako ta suma ima beskonačno mnogo racionalnih sabiraka. Ovo jednostavno nije tačno. Svaki realan broj je predstavljiv kao limes niza racionalnih brojeva. Nauči najpre teoriju realnih brojeva. O tome nemam nameru da se raspravljam, već samo mogu da ti preporučim literaturu. [ Ivan Dimkovic @ 02.04.2011. 11:29 ] @
@Gost,
Sa formulom mozes saznati koliko god zelis cifri broja PI - kao sto Nedeljko rece, imati tu formulu je isto sto i imati znanje o tom broju matematicki. Fizicki, naravno, ogranicen si fizickim zakonima - pa je broj cifri broja PI koje mozes znati u konacnom vremenu konacan. Ocigledno te bune ta 2 vrlo razlicita slucaja - matematicki, i fiziki "realan" za nase smrtne mozgove koji moraju da postuju fizicke zakone. [ Ivan Dimkovic @ 02.04.2011. 14:52 ] @
Čudan je tiganj ta beskonačnost. Kupiš piletinu i usitnjavaš je u sve sitnije i sitije parčiće i na kraju u tom tiganju dobiješ pečenog goluba!!!
Ništa čudno - pile je realna ptica i golub je realna ptica. U tom tiganju možeš dobiti pticu po želji zavisi samo od načina (formule ili recepta) na koji usitnjavaš piletinu. [ SrdjanR271 @ 02.04.2011. 15:07 ] @
Citat: The infinite! No other question has ever moved so profoundly the spirit of man; no other idea has so fruitfully stimulated his intellect; yet no other concept stands in greater need of clarification than that of the infinite. David Hilbert [ SrdjanR271 @ 02.04.2011. 16:45 ] @
Samo sam hteo da pokažem do kakvog apsurda dovode proizvoljna tumačenja beskonačnosti od strane nekih matematičara.
[ Nedeljko @ 02.04.2011. 19:02 ] @
Ajde leba ti, prvo nauči nešto matematike, pa onda iznosi mišljenja.
[ kandorus @ 02.04.2011. 19:17 ] @
^Gost
Koji matematičar je usitnjavao piletinu da bi dobio goluba? [ SrdjanR271 @ 02.04.2011. 19:19 ] @
Gostov paradoks (piletina-golub conjecture)
[ edisnp @ 02.04.2011. 21:24 ] @
Ja stvarno dosad nisam cuo sa Gostov paradoks jedino
ako to nije nesto novo otkriveno xD [ petarm @ 02.04.2011. 22:08 ] @
Kad postoji Studentova raspodela, sto da ne i Gostov paradoks
[ petarm @ 03.04.2011. 05:51 ] @
Citat: kandorus: Koji matematičar je usitnjavao piletinu da bi dobio goluba? Ovi ovde! Po njima je beskonačnost generator transcendentnih brojeva. Oni ne shvataju da transcendenti broj nije član ni jednog racionalnog niza koji mu se približava niti može postati član toga niza - on je jednostavno drukčiji. Principijelna razlika između kokoši i goluba je manja nego između racionalnih i transcendentnih brojeva. [ petarm @ 03.04.2011. 08:07 ] @
Meni se cini da ti koristis KAMADJOZA princip da bi pricao o razlikama izmedju racionalnih i iracionalnih brojeva.
[ petarm @ 03.04.2011. 13:05 ] @
Koji li tek ti princip koristiš kad poistovećuješ razliku između brojeva sa različitošću brojeva - očigledno ne umeš precizno
da kažeš to šta hoćeš. [ petarm @ 03.04.2011. 13:53 ] @
KAMADJOZA princip je skracenica za kako mali Djokica zamislja. Hocu da kazem da bi se doslo do slicne rasprave i do slicnih tvojih zakljucaka i da ti je neko rekao da je skup prirodnih brojeva
 prebrojiv. Niko od nas ne moze da izbroji sve prirodne brojeve, ali skup prirodnih brojeva je ipak prebrojiv. Ne mozes odrediti sve cifre broja prebrojiv. Niko od nas ne moze da izbroji sve prirodne brojeve, ali skup prirodnih brojeva je ipak prebrojiv. Ne mozes odrediti sve cifre broja  , ali sve cifre broja , ali sve cifre broja  su jasno definisane. Jako je puno sranja nastalo kada su filozofi pokusali da interpretiraju pojmove u fizici kao sto su relacije neodredjenosti, ... Ne mislim ja da ti lose mislis, samo ne mislim da mozes za ovo traziti neke primere u prirodi. Ali broj kao broj je uveden aksiomatski i teorijom brojeva se bave matematicari. Za racune u fizici i elektrotehnici je sasvim dovoljno uzeti prvih su jasno definisane. Jako je puno sranja nastalo kada su filozofi pokusali da interpretiraju pojmove u fizici kao sto su relacije neodredjenosti, ... Ne mislim ja da ti lose mislis, samo ne mislim da mozes za ovo traziti neke primere u prirodi. Ali broj kao broj je uveden aksiomatski i teorijom brojeva se bave matematicari. Za racune u fizici i elektrotehnici je sasvim dovoljno uzeti prvih  cifara broja cifara broja  ili ostaviti prosto ili ostaviti prosto  u krajnjem izrazu. u krajnjem izrazu. [ Shadowed @ 03.04.2011. 14:36 ] @
@Gost, galet, ti li si? :)
[ SrdjanR271 @ 03.04.2011. 17:20 ] @
Mislim da je vreme da se pređe na broj e.
[ edisnp @ 03.04.2011. 17:48 ] @
I sad ako predjemo na broj
 gde ce na kraj bit gde ce na kraj bitali evo da bude tema sto interesantija kao sto je svima vec poznato broj 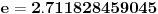 je jedna od najvaznijih matematickih konstanti je jedna od najvaznijih matematickih konstantikoja ima mnoge primene.Za njegovo uvodjene potrebno je najpre dokazati izvesne nejednakost, cije dokaze ostavljam mnogo vecim matematicarima od mene Dakle ...... [ edisnp @ 03.04.2011. 18:33 ] @
Izvinjavam se pogrijesio sam prevideo sam nekoliko cifara
nista strasno. [ SrdjanR271 @ 03.04.2011. 18:34 ] @
[ petarm @ 03.04.2011. 19:59 ] @
Citat: SrdjanR271: Specijalno za gosta. 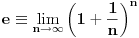 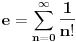 @edisnp Nema veze za tebe, ali u Gostovoj analizi sa takvim brojem e moze se doći do Gostove nejednakosti. I ovde Gost moze lepo da vidi kako je jedan iracionalan broj jednak beskonacnoj sumi racionalnih. [ petarm @ 03.04.2011. 20:04 ] @
Citat: Rade Doroslavacki, profesor na FTN-u Novom Sadu, da bi se pravio vazan napise 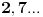 Zatim 1828. je rodjen Tolstoj 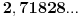 pa jos jednom godina rodjenja Tolstoja 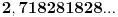 a kad ste to zapamtili mozete i  Naravno on samo dopisuje brojeve. Ja sam ovako stavio da bude preglednije. I kad to napise neki studenti krenu da ovo proveravaju na kalkulatoru. http://sr.wikipedia.org/sr/%D0...%D0%BB%D1%81%D1%82%D0%BE%D1%98 Ne znam zasto sam vam ovo napisao, ali ne moze da skodi. A sto ne skodi koristi :) Sad mozda zapamtite kad je rodjen Tolstoj pa iskoristite na nekom kvizu :) [ petarm @ 03.04.2011. 23:06 ] @
[ SrdjanR271 @ 03.04.2011. 23:29 ] @
[ kandorus @ 04.04.2011. 01:32 ] @
Ovde više nije pitanje definicija i rezultata. Pravo pitanje je kako objasniti nekome da od racionalnih brojeva može dobiti iracionalan broj. Matematičari se takvim objašnjenjima ne bave jer njih interesuje samo rezultat matematičkih operacija i dokaz da odredjene operacije daju traženi rezultat.
Način da se reši ovaj problem je da se uoči da matematički objekti svoju egzistenciju crpe iz matematičkih osobina i relacija kojima su povezani. "Realističko" posmatranje broja kao "stvari za sebe" nije primereno matematici. Iracionalni broj je rezultat matematičke operacija koje se vrše ali izgleda da nije zgodno reći da se dobija od racionalnog broja. Posmatranjem niza umetnutih intervala dolazi se do jedne tačke koja se nalazi u svakom od tih interval. Ta je tačka jedinstvena (dužina intervala teži nuli pa na rastojanju nula ne mogu postojati dve tačke) i može biti racionalna ili iracionalna. Da bi smo shvatili kako smo vršeći operacije nad racionalnim tačkama došli do iracionalne tačke treba uočiti da smo u stvari samo eliminisali racionalne tačke. Dakle nismo racionalne tačke nekim matematičkim operacijama "pretvarali" u iracionalnu već smo koristili matematičke operacije da eliminišemo racionalne tačke (In = a-n gde je a brojna osnova, In dužina intervala n). Na kraju, ono što je preostalo, je iracionalna tačka. Ovo se može detaljnije izložiti ali o tome postoji literatura pa se ne bih zadržavao. [ kandorus @ 04.04.2011. 07:12 ] @
Raduje me što konačno čujem glasove razuma.
[ Nedeljko @ 04.04.2011. 07:30 ] @
Hajde, idi na taj kontrolni i dobi tog keca koga si zaslužio.
[ kandorus @ 04.04.2011. 08:27 ] @
Šta se postiže takvim "savetima"?
[ Nedeljko @ 04.04.2011. 08:43 ] @
Čovek govori sa visine o nečemu o čemu nema pojma, tvrdeći da najveći matematički umovi nemaju pojma, već da je samo on pametan, a ne zna ni najosnovnije stvari, jer kako i sam uviđa, upravo mu se smeši kec na kontrolnom iz matematike.
A što se tvoje prethodne godine, ti bi da rešiš neki nepostojeći "ptoblem" u matematici preko filozofije, što govori o tvom razumevanju matematike. [ Nedeljko @ 04.04.2011. 09:08 ] @
Citat: Nedeljko: Čovek govori sa visine o nečemu o čemu nema pojma, tvrdeći da najveći matematički umovi nemaju pojma, već da je samo on pametan, a ne zna ni najosnovnije stvari, jer kako i sam uviđa, upravo mu se smeši kec na kontrolnom iz matematike. Pogrešio si junače. Ja nisam taj gost nego tvoj stari poznanik kome nikad i ni za šta nisi dao uverljiv odgovor. [ Nedeljko @ 04.04.2011. 09:23 ] @
Aha, zato se kriješ pod plaštom anonimnosti. Blam te je prethodnog imena "galet@world", odnosno "Dane Gaćeša". Ja se ne stidim da svoje stavove iznosim pod svojim punim i pravim imenom i prezimenom.
Siguran sam da bi i ti dobio keca na istom onom kontrolnom. Slažem se da ti možda nikada nisam dao odgovor koji bi tebi bio prihvatljiv, jer tebi je u svom tvom neznanju i oholosti prihvatljivo samo ono što ide u prilog "tvojoj veličini". [ kandorus @ 04.04.2011. 09:43 ] @
^Nedeljko
Pregledao sam moje komentare ali nisam se pozvao na filozofiju i nisam rešavao nepostojeći "ptoblem" kako ti kažeš. "ptoblem" možda jeste nepostojeći u smislu da napred pomenuti redovi zaista daju traženi rezultat ali preterivanje je da se čoveku na taj način obraća ako mu nije jasno neko objašnjenje. Čemu onda služi matematika? Samo se dogma ne kritikuje a matematika treba redovno da proverava svoje rezultate. Drugo, mogao si čoveku pomoći kad već znaš šta i kako. No, čini se da si ti dobar u bubanju napamet mehaničkih šema ali se ne snalaziš kad to treba primeniti na nestandardna pitanja. E, da, kako se logujete sa tim "Gost", hoću i ja. Xa Xa Xa [ Nedeljko @ 04.04.2011. 09:58 ] @
Što se proveravanja tiče, zna se kako se zasniva matematika. Šta misliš kako osnove matematike proveravaju ozbiljni istraživači koji se time bave? Ovakvim naklapanjima sigurno ne.
Citat: kandorus: Drugo, mogao si čoveku pomoći kad već znaš šta i kako. Problem je u tome što on ne želi da mu se bilo šta objasni, nego da on nama objasni, a nema pojma. Da je hteo nešto da nauči, mogao sam da ga uputim, ali on to ne želi i onda mu ja ne mogu pomoći. [ Nedeljko @ 04.04.2011. 10:14 ] @
@ Nedeljko Danas mi je izuzetno prijatan dan a tome su doprineli Đoković, SrdjanR271, kandorus i naročito ti. Ti, zato što me nisi pohvalio, jer bih to smatrao tragedijom. [ kandorus @ 04.04.2011. 10:25 ] @
Ja sam problem pokušao da sagledam iz ugla nekoga ko tek usvaja znanje. I tada smatram da treba tražiti povoljniji pristup za studenta. A pored toga od suštinske je važnosti kako izlagati neku materiju i predvideti koje rezltate (u shvatanju problema) može da pruži odredjeni metod prezentiranja gradiva.
Tačno je da sve to piše u knjigama. Medjutim učenje matematike kod nas se ne zasniva na proučavanju literature već na usvajanju gradiva izloženog na predavanju. To je dosta jednostrano. Mnogo bolje bi bilo da se studentu za svaku lekciju eksplicitno navede literatura koju mora proučiti za savladavanje te lekcije. Kod nas se podrazumeva da se pročita knjiga predavača ali to je jednostrano jer je predavač već dao svoje vidjenje a njegova knjiga nije ništa drugo nego to isto vidjenje, dakle jednostrano ma kako bilo dobro. Nije dovoljno reći "eno spisak literature na kraju knjige", već nedvosmisleno za svaku porciju gradiva šta i gde proraditi i to u "sitna crevca". Ako bi student za svaku lekciju morao iznova da konsultuje spisak od 20-30 knjiga navedenih u odeljku "literatura" to bi bilo kontraproduktivno i ne bi vodilo ničemu. U tome je smisao fakulteta da usmeri studenta kojim putem treba usvajati gradivo. Drugi fakulteti su imali dobru praksu da se savladavanje gradiva zasniva na proučavanju literature (plus predavanja). Kolokvijumima se proverava urednost proučavanja literature i student umesto bubanja u potpunosti sagledava gradivo. Ne znam da li je i danas tako jer sve više knjiga pišu predavači (bar ono što vidim po knjižarama) i učenje se opet svodi na indirektno bubanje predavanja. [ Shadowed @ 04.04.2011. 10:45 ] @
Kandorus, ok je to sve, al' ono sto je Nedeljko video a ti ne je o kome se zapravo radi.
Galet je jedini za ovih 10god koliko ES postoji koji je uspeo da bude banovan zbog troll-ovanja na matematici i fizici. [ edisnp @ 04.04.2011. 10:55 ] @
Znaci li to da je i ovo on http://www.elitesecurity.org/t426645-Lose-Hitno-pomoc
[ Shadowed @ 04.04.2011. 11:39 ] @
Ne znaci. "Gost" je upisano na mesto nick-a kada neko postuje neulogovan. To je dozvoljeno samo na nekim forumima (npr. predlozi i pitanja, it berza poslova i sl.). Iz nekog razloga poslednjih mesec-dva je dozvoljeno i na matematici. Prijavljeno je pa se ceka da neko od admina popravi.
[ Nedeljko @ 04.04.2011. 11:57 ] @
Citat: edisnp: Znaci li to da je i ovo on http://www.elitesecurity.org/t426645-Lose-Hitno-pomoc Izgleda da nije, a nije ni jedini koji je banovan zbog trolovanja. Čak mi nije ni poznato da je banovan. [ Nedeljko @ 04.04.2011. 11:59 ] @
Citat: Gost: @ Nedeljko Danas mi je izuzetno prijatan dan a tome su doprineli Đoković, SrdjanR271, kandorus i naročito ti. Drago mi je ako si raspložen, a još draže ako sam ja doprineo tome. Želim ti sve najlepše. [ Nedeljko @ 04.04.2011. 12:01 ] @
@kandorus
Sve je to lepo što pišeš o spuštanju na nivo studenta, ali ovde se radi o nekome ko odbija da bude student, već isključivo profesor i to ne neki normalan, koga možeš i da ispraviš kada pogreši, nego neko odbija svaki input i ima samo output. [ igorpet @ 04.04.2011. 12:11 ] @
Od broja
 do pozdrava i cestitki do pozdrava i cestitki Simpaticno je gledati kako ljudi diskutuju o necemu sto je otkriveno i definisano pre vise od 2.000 godina ... sa argumentima koje bi skoro i sam Arhimed mogao lako da pobije ... Poenta je otkriti nesto cime bi se ljudi zanimali sledecih 2.000 godina (ako prezivimo kao vrsta toliko) a ne pobijati i izvrtati ono sto je vec dokazano ... [ igorpet @ 04.04.2011. 12:18 ] @
Banovan sam zato što sam jednom važnom čoveku zbog neobjašnjenog brisanja teme uputio preoštre reči.
To priznajem - nije trebalo, ali bio sam revoltiran. Takođe mislim da je banovanje bila preoštra kazna. Ali šta je tu je. Kako ja trolujem i da li uopšte trolujem vidi se i na osnovu ove teme pa procenite sami. Nedeljko, zahvaljujem na lepim rečima. I ja tebi želim sve nabolje. Naše čarke su sporedna stvar. [ Nedeljko @ 04.04.2011. 12:33 ] @
[ Nedeljko @ 04.04.2011. 13:58 ] @
Naravno, jednak je 1(π).
[ edisnp @ 04.04.2011. 19:32 ] @
I eto dodjosmo i do kraja ove jedne vrlo lijepe i korisne komunikacije
medju clanovima ovog foruma kad sam postavljo ovu temu nisam ni sanjo da je ce bit preko sto odgovora svaka cast ljudima na tolikoj aktivnosti. [ SrdjanR271 @ 04.04.2011. 22:20 ] @
Za broj kakav je Pi sto odgovora je zanemarljivo :D
A bogami i e [ maksvel @ 04.04.2011. 22:22 ] @
Hajde sad idemo na novu priču - kako je Nedeljko "namikerio" da postane član broj 100 pi na Es-u??
I da li to ima veze što ima dva e u imenu?? Itd. [ edisnp @ 04.04.2011. 23:07 ] @
Mislim da ti to pitanje veze nema
[ edisnp @ 04.04.2011. 23:10 ] @
[ SrdjanR271 @ 04.04.2011. 23:22 ] @
Slobodno pokreni meni je to jako zanimljivo. Samo da se ne pojave neki koji će tvrditi da je e racionalan.
Tema može da se zove broj e istina ili mit :D [ URUS @ 09.04.2011. 22:50 ] @
Privet vsem !
Vot čislo 'pi'. Esli vam interesno znatь s točki zreniя matematiki. Ssыlka na faйl: http://webfile.ru/5252232 Imя faйla: Vezdesuщee čislo 'pi'.zip Razmer: 2 Mb [ edisnp @ 09.04.2011. 23:20 ] @
Moze li neko da prevede posto ne znam Ruski.
[ SrdjanR271 @ 10.04.2011. 01:20 ] @
G. Translate
[ edisnp @ 10.04.2011. 02:29 ] @
Meni nece da prevede ovo sa Ruskog na Srpski a nije ni bitno.
[ Nedeljko @ 10.04.2011. 09:21 ] @
[ Nedeljko @ 10.04.2011. 09:42 ] @
Što se prevoda tiče, problem je što je Gojko mrzitelj ćirilice, pa treba sve vratiti na ćirilicu pre prevođenja. Evo šta meni kaže Google Translate:
 [ kandorus @ 10.04.2011. 10:28 ] @
Reč je o knjizi Žukova u kojoj je dato dosta zanimljivosti o broju Pi. Ne samo kao matematčka konstanta već je povezan sa mnogim prirodnim konstantama. Na primer Pi² ≈ g.
^Nedeljko Kako je sqrt(2)+sqrt(3) = Pi? [ Ivan Dimkovic @ 10.04.2011. 10:40 ] @
Mislim da je Nedeljko samo bio sarkastican - na nivou diskusije tj.
[ Sini82 @ 10.04.2011. 11:52 ] @
Slažem se.
[ edisnp @ 10.04.2011. 12:15 ] @
Mislim da je malo gruba rec SARKASTICAN.
[ pitomir @ 13.04.2011. 11:26 ] @
[ miki069 @ 13.04.2011. 11:39 ] @
Zbir beskonačnog geomerijskog reda koji konvergira je S=a1/(1-q).
[ kandorus @ 13.04.2011. 13:15 ] @
Σ(-x2)n = (-x2)0 + (-x2)1 + (-x2)2 + (-x2)3 + ... = 1 - x2 + x4 - x6 + ...
1/(1 + x2) = ( 1 + x2 - x2 ) / (1 + x2) = 1 - x2 / (1 + x2) = 1 - (x2 + x4 - x4 ) / (1 + x2) = 1 - ( x2(1 + x2) - x4 ) / (1 + x2) = 1 - x2 + x4 / (1 + x2) = ... = 1 - x2 + x4 - x6 + ... = Σ(-x2)n [ SrdjanR271 @ 13.04.2011. 16:17 ] @
[ pitomir @ 13.04.2011. 20:22 ] @
Sad mi je jasno. Hvala svima :)
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|