Da probam

Za









<sub>[Ovu poruku je menjao SrdjanR271 dana 30.03.2011. u 23:44 GMT+1]

[Ovu poruku je menjao SrdjanR271 dana 30.03.2011. u 23:45 GMT+1]</sub>

Tačno za , netačno za . Inače, tako se dokazuje ono što onako hoće.

Moja greška p je između 1 i beskonacno. Ispravio sam.

Hvala puno.
Lepota je u jednostavnosti.

Zanima me dalja implikacija za datu pretpostavku
a + b > 2c
moze li se dokazati da je za vrednosti p[0, 1] relacija

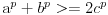
odgovara? Uz gore navedeni sled dokaza, dobijamo

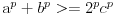
Ocigledno je exponent na konstanti 2 odlucujuci, i za vrednosti p=[0, 1], 2^p =[1 ,2].
Ukoliko je p=0, dobijamo jednakost (zbog toga >=). Ukoliko je
u inicijalnoj pretpostavci a + b >= 2c, p iz intervala [0, 1], onda se zahtev ne odgovara, izuzev p=0;

Interesuje me da kakav raspored (distribuciju) vrednosti a, b, c, relacija

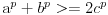
odgovara uz datu pretpostavku a + b > 2c. Znaci li da ukoliko su a, b, c veci od 2, velika je verovatnoca
da relacija sledi?

Zahvaljujem

Ovo se može dokazati na isti način kao i ono sa početka teme.

_{[Ovu poruku je menjao SrdjanR271 dana 02.04.2011. u 17:25 GMT+1]}

To sam i naveo u prethodnom postu.
No, zanima me uslov kada konstanta 2 ne ulazi u exponent operaciju (vidi gore).
Ukoliko se to ne moze dokazati, izuzev za p=0, interesuje me za kakvu relaciju a, b, c
vrednosti (distibucija, najmanja vrednost, ...) postoji veca verovatnoca da
nova relacija (gore navedena) vazi.

Za sad nemam ideju kako bi to moglo, osim ako je a+b>(2^p) c, p>1

Interesuje me verovatnoca da je relacija ok u datim uslovima.
Npr, za p=0, relacija uvek vazi.

Da li je tako i ako je a>c i/ili b>c; ili a+b>>c (zbir prilicno veci od c, ili pojedinacne vrednosti).

Na primer,

data je nejednakost a+b>2c; uz _pretpostavku_ ab>=c^2 moze se dokazati
da je (za exponent p=0.5)

sto je upravo ono sto trazim. Moze li se postaviti neka _pretpostavka_, kao gore
navedena, tako da vazi (za 0<p<1 )

Iz sledi

.

Uslov uopšte nije potreban.

Uslov je potreban, obavezan. Na osnovu njega kreiram drugi (kao npr. ab>c^2), tako da je
a^p+b^p>=2c^p, za p=0.5.
Pitanje je: za kakav kreiran uslov (vidi gore) relacija
a^p+b^p>=2c^p
vazi za 0<p<1.
Kreirani uslov ab>c^2 je za p=0.5, ali nisam siguran koji je za p u intervalu [0,1].
Moze li se tako nesto uopste postici?

Npr.
Uz pretpostavku


moze li se dokazati da je

Mozda bi izraz za (a+b)^p bio od koristi. Hvala

<sub>[Ovu poruku je menjao onako dana 06.04.2011. u 16:17 GMT+1]

[Ovu poruku je menjao onako dana 06.04.2011. u 16:18 GMT+1]

[Ovu poruku je menjao onako dana 06.04.2011. u 16:18 GMT+1]</sub>

Obzirom da je moje sledece pitanje vezano za ovu temu, nastavljam ovde.
Moze li se dokazati relacija

za a,b>=1 i p=[0,1]? Naravno, za p=1 mogu koristiti kvadrat binoma.

Zahvaljujem

Posle smene , nejednakost se svodi na za .