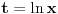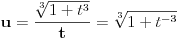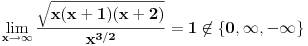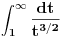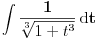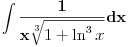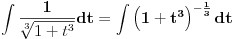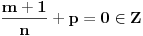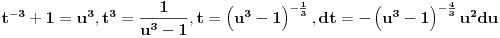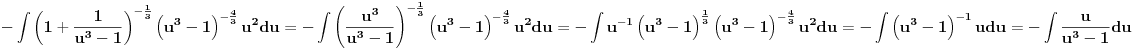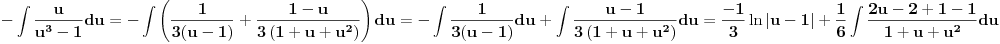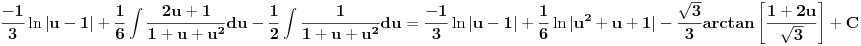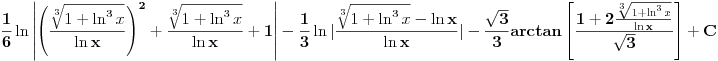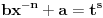Mislim da se drugi ne može rešiti preko elementarnih funkcija.

Treći konvergira.

U drugom najpre ide smena , a potom . Dobija se integral racionalne funkcije po .

U trećem treba koristiti poredbeni kriterijum. Obzirom da je , a konvergira, onda dati nesvojstveni integral konvergira.

Ih ...

Prvo ide smena lnx=t
.
.
.

a onda se primeni smena prema sledecim pravilima, kao sto je Nedeljko vec napisao

Ja sinoc probao u Mathematica 8 i ono izbaci neke AppelF1 hipergeometrijske redove.
Eto može i mathematica da pogreši. Izvinjavam se svima.

Ovako sam ja radio...



Kako si dobio pod korijenom t^-3?? I zasto je kod tebe u=(1+t^3)^(1/3)/t??

Kasnije sam radio kako je i "igorpet" naveo..

Kako ti je taj koren odjednom iskocio iz imenioca u brojilac (i tamo ostavio 1), pa je razlomak nestao?

Smena je ok, ali onda se trazi

To nije greška, već samo drugi oblik rešenja.

Bio bih zahvalan onome ko bi me podsetio kako se zove ovaj tip integrala.

Binomni diferencijal. (Čebišev)
Znam da je drugi oblik rešenja, ali ako ima primitivnu f-ju preko elementarnih, mathematica uvek daje rešenje bez specijalnih f-ja,
pa me je to navelo da pomislim da nema primitivnu izraženu preko elementarnih.

Pa, eto, ne daje. Ovo očigledno nije tačno.

Evo da i ja rešim
sad smena ln x=t, pa imamo

Sada može Čebišev pod 3)

Pa uzimamo smenu

Dalje imamo





KONAČNO


Koji smor od integrala.

Ja sam gost :) ne znam što me "logautovalo"

@vlado1991 sta studiras?

_{[Ovu poruku je menjao SrdjanR271 dana 01.04.2011. u 01:51 GMT+1]}

Nisam bio pri kompjuteru zadnjih par dana, pa se nisam mogao ni javiti.


A ovo sam ja, i mene izlogovao, zasto ne znam.. )
Da, vidim, greskom je "iskocio" iz imenioca u brojilac, pogresno sam zapisao zadatak.

@SrdjanR271
Studiram Elektro fakultet u PG. Sta mislite o tezini kolokvijuma, na skali od 1 do 10?? Da li je stvarno tezak, koliko ja mislim da jeste, ili bi ovo trebalo da ide "glatko"?

Samo je drugi komplikovan.

To zavisi od puno faktora. Zavisi sta ste radili na vezbama, kakvi su inace pismeni... Uvek je tesko ono sto ne znas, a lako ono sto znas. Nema nekih pravila.

Smena je u trećem slučaju

, gde je imenilac od .

Hvala na ispravci Nedeljko, nisam zagledao da je prevod lose odradjen (nisam ja prevodio)
Evo i nesto detaljnije isto ovo (jeste da je na ruskom ali mislim da se razume dovoljno):