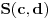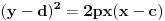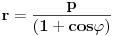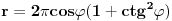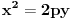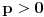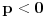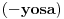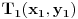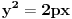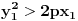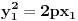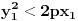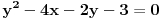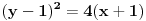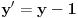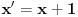[ PomocMata @ 10.04.2011. 12:25 ] @
| -Zdravo, imam jedan problem, trebam da napravim prezentaciju, tj. da objasnim sta je parabola, i povezanost parabole i farova na automobilu. Trazim vec sat vremena i nista korisno nisam nasao, pa ako mozete, objasnite mi sta je parabola (definicija, formula, sve cega se setite ) I da povezete parabolu sa farovima (koliko sam ukapirao, farovi imaju oblik parabole da bi svetlosni snop dalje dopirao, tako nesto) Ovo mi treba prilicno brzo, pa ako mozete da mi pomognete bio bih zahvalan. Unapred hvala, pozdrav |