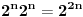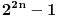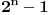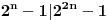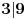Tada kvadrana tabla je dimenzija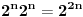
i kada joj odstranimo jedno polje dobicemo 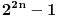polja ova
dole figura na slici nam je nekog oblika 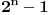i sad treba da dokazes
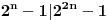ovaj izraz mozes dokazati vrlo lako indukcijom
da je deljivo 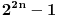ovo sa 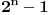ovim
i nakon sto to dokazes sledi da se moze tablica 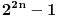poplocati
figurama kao na slici.

Drugi zadatak: Može, ali to što je edinsp napisao nije dovoljno, jer postoje figure površine 3 pomoću kojih se popločavanje ne može izvršiti (uzmi krugove na primer).

Neka je figura koja se sastoji od kvadrata 2x2 iz koga je izvađen 1x1 ćošak zove mala pločica, a slična duplo veća figura neka se zove veća pločica.

1. Veća pločica može popločati sa 4 male.
2. Ako se kvadrat dimenzija nxn bez ćoška 1x1 može popločati sa k malih pločica, onda se kvadrat 2nx2n bez ćoška 2x2 može popločati na isti način sa k velikih pločica, odnosno kvadrat 2nx2n bez ćoška 1x1 se može popločati sa k velikih pločica i jednom malom, pa samim tim i sa 4k+1 malih.

Naravno slazem se da ne moze sto se tice krugova ali ovde u zadatku
nije rec o krugovima nego je data konkretna slika za koju se postavlja pitanje.
Ne treba uzimati nisto sto u zadatku nije navedeno.

Tvoj argument nije dobar, jer se poziva samo na površine. Ako bi on bio dobar, bio bi primenljiv na ma kakve figure odgovarajućih površina, a nije.

Ako ti nije jasno o čemu pričam, pokušaj 3x3 kvadrat da popločaš onim figurama iz zadatka. 9 je deljivo sa 3, ali...

Pa bez obzira sto je 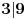ne moze se poplocati datim figurama.

Dakle, argumentacija samo na osnovu odnosa površina je dovoljna da dokažeš da popločavanje ne postoji, ali ne i za dokaz da postoji.

Naravno ali ima situacija i da je poplocavanje moguce pa sta onda
treba napisat kao resenje?

Dokaz da je moguće.

Hmmmm... Nedeljko je cini mi se u pravu, ne mogu da zakljucim samo na osnovu povrsine da ne mogu da pokrijem kvadratnu povrsinu figurom koja mi je data. Imate li neki drugi predlog? :)

Pa, možeš je popločati. Dao sam ti uputstva za dokazivanje.

Može se dokazati matematičkom indukcijom. Podijeli tablu na četiri kvadranta. Jedan je bez ćoška, može se pokriti po indukcionoj pretpostavci. Figuricu L sa slike stavi na pravo mjesto, tako da se nalazi u preostala tri kvadranta i pokriva njihove ćoškove. Dalje je lako.