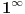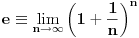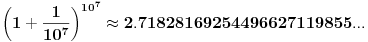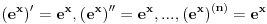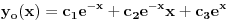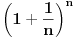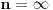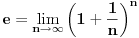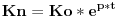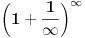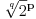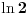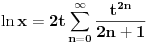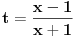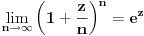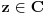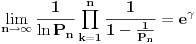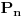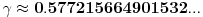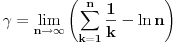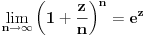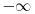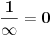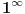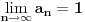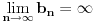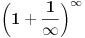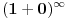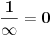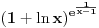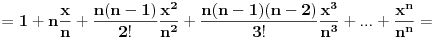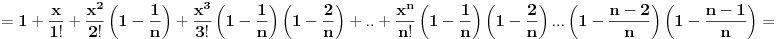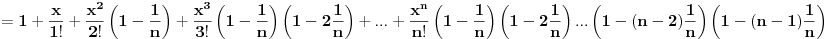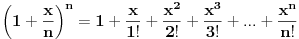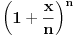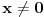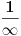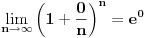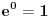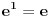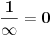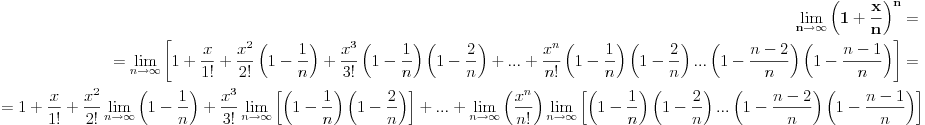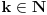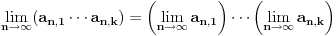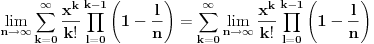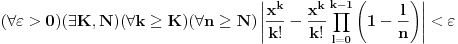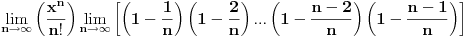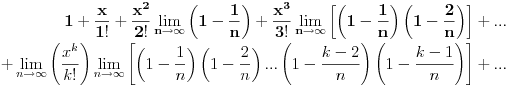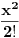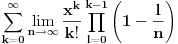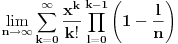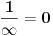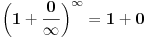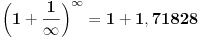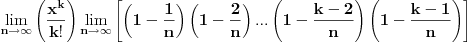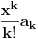|
|
[ fentalijana @ 12.04.2011. 17:47 ] @
|
| Kad sam ja išla u gimnaziju i kad nam je profesor iz matematike objašnjavao broj e
on je rekao da bi taj broj bio dobar za štediše. Ne sećam se baš tog objašnjenja, ali
čini mi se da je nešto rekao kao u smislu da se kamate odmah pretvaraju u glavnicu
ili tako nešto i još je nešto objašnjavao kako biljke rastu prema tom broju.
Zbog toga mi je taj broj zanimljiv, o to davno objašnjenje mog profesora nisam baš ni
onda razumela, a ne razumem ni sada pa ako bi neko hteo da mi to malo pojasni...
ali po mogućnosti bez puno formula nego onako nekako... bližim rečima.
Ako je e = (1 + 1/n)n kada je n = ∞ onda bi trebalo da bude e = 1 a ne 2,71828...
jer je 1/∞ = 0.
Ovo mi nikako ne ide u glavu pa bih zamolila pre svega Nedeljka, pa onda kandorusa
a i Gosta da mi objasne o čemu se tu radi i kako to oni shvataju. |
[ SrdjanR271 @ 12.04.2011. 18:37 ] @
Menjanje vrednosti n=  i limes ne znače isto.
Kod limesa 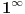 je neodređeno.
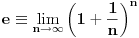
A što se ekonomije tiče preporučujem
http://poincare.matf.bg.ac.rs/~pavlovic/svetski_por.pdf[ SrdjanR271 @ 12.04.2011. 19:08 ] @
Probaj ovo 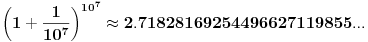 [ kandorus @ 12.04.2011. 21:15 ] @
U prirodi se procesi odvijaju po prirodnim zakonima pa je bolje reći "biljke rastu prema uvis". Nije mi poznato da postoji biljka koja raste prema broju e ali kod biljaka postoje strukture koje se mogu dovesti u vezu sa nekim brojevima. No to je posebna tema.
Ako hoćeš da izračunaš vrednost broja e koristi navedenu formulu. Ta formula kaže da tačna vrednost broje e je rezultat formule kad n postaje sve veće, toliko veliko da je veće od bilo kog broja. To je problem jer računanje je moguće samo do neke veličine broje a onda ili prekidamo ili "više nemamo papira" pa opet prekidamo.
Medjutim približnu vrednost možemo izračunati koristeći upravo tu formulu. Koliko tačno hoćemo da izračunamo vrednost broja e toliko velik broj uzimamo.
n=1
e ≈ e(1) = (1+1/1)^1 = 2
I to je već približno jer je e=2.71828182...
Da bi smo dobili tačniju vrednost broja e uzmemo
n=2
e≈(1+1/2)^2 = 1.5^2 = 2.25
Kao što se vidi povećanjem n nismo smanjili dobijenu vrednost nego smo je povećali. To znači da ta formula ne mora nužno da rezultira u (1+0)^n=1 jer u stvari povećanjem n vrednost dobijena formulom raste.
n=3
e≈(1+1/3)^3 = 1.3333...^3 ≈ 2.37037037
n=4
e≈(1+1/4)^4 ≈ 2.44140625
Dakle, što veće n to smo bliže broju e.
Još se postavlja problem, kako znamo da vrednost dobijena za bilo koje n nije veća od vrednosti broja e?
Pokazaćemo nešto lakše: da vrednost broja e sigurno nije veća od recimo 3.
Broj e se može izračunati i po formuli:
e = 1 + 1/1 + 1/2 + 1/6 + 1/24 + ... + 1/k! + ...
gde je k! = 1 * 2 * ... * k.
Za proizvoljno veliko n>2 važi (proveri)
e(n) = 1 + 1/1 + 1/2 + 1/6 + 1/24 + ... + 1/n! < 1 + 1 + 1/2 + 1/4 + 1/8 + ... + 1/2^(n-1) =
= 1 + (1 – 1/2^n)/(1 – 1/2) = 1 + 2(1 – 1/2^n) < 3
jer je (1 – 1/2^n) < 1 pa je 2(1 – 1/2^n) < 2 itd. Zaključujemo da je vrednost broja e negde izmedju 2 i 3.
Postoje mnoge primene broja e. Na primer u biologiji se može koristiti da se izračuna broj ćelija po formuli
N(t)=N(0)*e^(w*t)
gde je
N(0) - broj ćelija u početnom momentu
N(t)- broj ćelija nakon vremena t.
w - odredjuje brzinu rasta.
U fizici i hemiji kod radikalskih reakcija itd.
Kakve veze ima broj e i obračun kamatne stope? Pretpostavimo da se kamata obračunava na glavnicu od 1 dinar u iznosu 100% na kraju godine. Tada se ukupno plaća 2=e(1) dinara. Ako se kamata obračunava dva puta godišnje tada se ukupno plaća 1*1.5^2=e(2)=2.25 dinara. Ako se kamata obračunava 4 puta godišnje tada se ukupno plaća 1*1.25^4 = e(4) = (1+1/4)^4 ≈ 2.44140625, itd.
[ SrdjanR271 @ 12.04.2011. 21:33 ] @
Da nema broja e mnoge diferencijalne jednačine ne bi bile rešive.
To je zbog sledećeg:
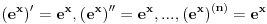
Npr. difierncijalna jednačina y'''+y''-y'-y=0 ima opšte rešenje 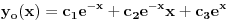 [Ovu poruku je menjao SrdjanR271 dana 12.04.2011. u 22:45 GMT+1]
[Ovu poruku je menjao SrdjanR271 dana 12.04.2011. u 22:45 GMT+1][ Nedeljko @ 12.04.2011. 22:34 ] @
Citat: fentalijana: Ako je e = (1 + 1/n)n kada je n = ∞ onda bi trebalo da bude e = 1 a ne 2,71828...
jer je 1/∞ = 0.
Ne,  nije 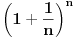 za 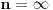 , već je 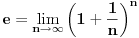 . Obnovi definiciju limesa. [ miki069 @ 13.04.2011. 07:21 ] @
Prekidno kapitalisanje podrazumeva da se kamata pripisuje glavnici kapitala tek posle isteka "obračunskog perioda".
Posle isteka n obračunskih perioda (m je broj obračunskih period u jednoj godini, p kamatna stopa na godišnjem nivou, t proteklo vreme), krajnja vrednost kapitala je:

gde je n = m*t
Pošto kapital ima uvećanu vrednost za kamatu i posle isteka 1 sekunde, onda m teži u beskonačnost i rešavanjem limesa, dobija se
krajnja vrednost neprekidnog kapitalisanja posle isteka vremena t:
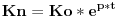
Znači u pravu je profesor i broj e je stvarno dobar za štediše.
Omogućava im da izračunaju vrednost kapitala u bilo kom trenutku.
[Ovu poruku je menjao miki069 dana 13.04.2011. u 12:42 GMT+1][ fentalijana @ 17.04.2011. 10:52 ] @
Vi ste se zaista potrudili, ja se zahvaljujem. Čekala sam da i Gost iznese svoje mišljenje,
ali, eto, nije. Zavezo mu se jezik. Pojela maca?
Bilo bi interesantnije jer bi se on, po svoj prilici, usprotivio pa bi diskusija bila mnogo
življa.
Kandorus je imao strpljenja da detaljno objasni broj e, ali mi se čini da nije sasvim u
pravu za biljke zato što se i kod biljaka njihov priraštaj odmah pretvara u veličinu biljke,
a veća biljka opet ima veći priraštaj i t. d. To bi bolje objasnio miki069 jer on kao i ja
“navijamo” za profesora.
Nedeljko me zbunio. Ja nisam baš tolika neznalica da ne znam šta je limes. On kaže da
je broj
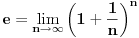
i ja to razumem, ali ne razumem ovo što je napisao da nije e. Ako nije e neka je neki
drugi broj, na primer neka je r pa je
 = 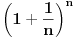 za 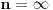
ili ovako:
 = 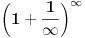 za 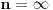
Sad ja ne znam kakav je to broj koji nije e, i ne znam šta pretstavlja taj broj i da li je
to uopšte broj. Sme li se tako pisati? Da li je tako napisan broj strogo određen ili nije? [ Nedeljko @ 17.04.2011. 17:25 ] @
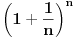 za 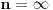 se sme pisati kao  . No, da vidimo koliko to iznosi:
 , a to je nedefinisano. Dakle, nema puno veze sa brojem  . [ kandorus @ 17.04.2011. 19:05 ] @
Citat: fentalijana
Kandorus je imao strpljenja da detaljno objasni broj e, ali mi se čini da nije sasvim u
pravu za biljke zato što se i kod biljaka njihov priraštaj odmah pretvara u veličinu biljke
Naveo sam da se broj e može povezati sa brojem ćeliija (a time i sa masom biljke). No to ne znači da broj e odredjuje kako će biljka rasti.
Rast biljke odredjuju prirodni faktori - vlažnost, temperaturura, zemljište, itd, itd. Na primer, ako nema dovoljno vlage da transportuje minerale iz korena u stablo džaba broj e, biljka staje s rastom. [ zzzz @ 17.04.2011. 23:33 ] @
Kada niko nije znao za broj e,a znali su šta je to eksponencijalna funkcija,neko je otkrio da za te funkcije vrijedi jedno interesantno pravilo:-Povucimo u bilo kojoj tački grafa takve funkcije tangentu i pogledamo gdje siječe x osu.Udaljenost ove tačke od vrijednosti x odabrane ordinate je uvijek ista.Ispada da je tangens ugla tangente proporcionalan sa vrijednosti funkcije.Dakle sadašnjim riječnikom rečeno prvi izvod je proporcionalan samoj funkciji.Neko se sjetio da ispita kad je taj koeficijent proporcionalnosti jednak 1.Za koju vrijednost baze eksponencijalne funkcije je to tako?"e" je jedinična baza eksponencijalnih funkcija.
[ Nedeljko @ 18.04.2011. 10:25 ] @
Kako izračunati približnu vrednost izaza 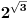 ? Jedan način je da se nađe racionalna aproksimacija  broja 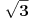 i da se onda izračuna 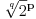 . Drugi, efikasniji način je preko reda
 .
Međutim, za to nam treba konstanta 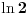 . Ona se može računati po formuli
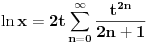 za 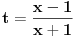 .
Eto kako se od proizvoljne osnove dolazi do osnove  .
[Ovu poruku je menjao Nedeljko dana 18.04.2011. u 14:00 GMT+1][ kandorus @ 18.04.2011. 10:47 ] @
Da li bi hteo da nam pokažeš kako si došao do jednakosti
 ? [ Nedeljko @ 18.04.2011. 11:00 ] @
Za  važi
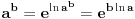 . [ kandorus @ 18.04.2011. 12:05 ] @
[ Nedeljko @ 18.04.2011. 13:00 ] @
Hvala, ispravljeno.
[ atelago @ 18.04.2011. 18:46 ] @
Vazi li ova jednakost?

[ zzzz @ 18.04.2011. 22:15 ] @
Citat: kandorus: Da li bi hteo da nam pokažeš kako si došao do jednakosti
 ?
Razvij 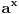 u Tejlorov red. [ kandorus @ 18.04.2011. 23:48 ] @
Ne znam št6a hoćeš da kažeš. To smo već razjasnili.
[ Nedeljko @ 19.04.2011. 08:34 ] @
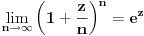 za svako 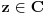 . [ kandorus @ 19.04.2011. 10:09 ] @
Mmm, da. Sad sam se setio. U vreme dok još nije bilo svih tih čuda tehnike upotrebljavane su Logaritamske Tablice. U njima su dati logaritimi sa osnovom 10.
Tada
e = 1o1/ln10
ew = 1ow/ln10
Zato umesto
Nt = N0ewt
zamenom k=w/ln10 korišćeno je
Nt = N01okt
Pa pozdravi profesora jer "biljke rastu prema broju 10".
U stvari, dugo (kao i danas) je primenjivana formula sa dekadnim eksponentom pa je istorijski put geneze formule bio obrnut, tj od stepena sa osnovom 10 do stepena sa osnovom e. Iz eksperimentalnih podataka konstruisani su dijagrami (na milimetarskom papiru) a dobijena prava linija je bila pogodna za lako očitavanje.
[ SrdjanR271 @ 19.04.2011. 16:18 ] @
Možda najlepša f-la 
I jedna jos luđa 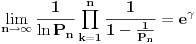 , 
Gde je 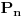 n-ti prost broj.
A 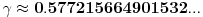 Ojler-Maskeronijeva konstanta
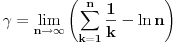 [ atelago @ 19.04.2011. 19:52 ] @
Ako bismo u ovu formulu
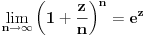
stavili da je z = 0 onda bi to odgovaralo katastrofalnoj suši, zar ne,jer bismo dobili e 0 = 1,
t.j. biljka stagnira nema prirasta, a osim toga profesor bi mogao da za bilo kakve uslove nađe
odgovarajući eksponent z i da ga u skladu sa uslovima menja tokom godine.
[ miki069 @ 19.04.2011. 23:31 ] @
Gde god je priraštaj dF direktno proporcionalan trenutnoj vrednosti veličine F (ne njenom kvadratu F^2 ili nečemu drugom) dobija se e:
dF = F*svašta
dF/F = svašta
ln(F) = integral (svašta) + C
F = K*e^(integral od svašta)
[Ovu poruku je menjao miki069 dana 20.04.2011. u 01:29 GMT+1]
[ zzzz @ 20.04.2011. 00:26 ] @
Kada zategnemo konopac on zbog svoje težine neće biti ravan već
povijen.U svakoj tačci tog konopca horizontalna komponenta sile je konstanta i jednaka je sili zatezanja konopca.To jako liči na konstantu
subtangente kod eksponencijalnih funkcija.Rješenje diferencijalne jednačine to dokazuje.
[ atelago @ 21.04.2011. 11:10 ] @
Nedeljko:

Ovo se može smatrati proizvoljnom ili čak pogrešnom tvrdnjom ukoliko se ne dokaže.
[ Nedeljko @ 21.04.2011. 11:36 ] @
Pa, dato ti je kompletno izvođenje. Naravno, korišćene su standardne operacije u pročirenom skupu realnih brojeva (konstantama  i 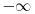 ).
Drugo je pitanje zašto su te operacije tako definisane, tj. zašto se radi baš sa takvim operacijama.
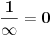 zato što je količnik niza koji teži jedinici i niza koji teži beskonačnosti niz koji teži nuli.
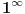 je nedefinisano jer ako je 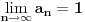 i 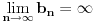 , limes od  može da bude svašta, pa i da ne postoji.
E, sad, tebi niko ne brani da definišeš neke svoje operacije na nekom skupu za koje će vaćiti drugačiji zakoni i da ih označiš nekim drugim simbolima. [ atelago @ 21.04.2011. 16:22 ] @
Da li je u zagradi binom 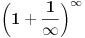 ili nije? [ edisnp @ 21.04.2011. 16:28 ] @
To bi trebalo da je jednako 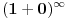 sto je jednako 
zato sto je 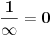 . [ SrdjanR271 @ 21.04.2011. 18:51 ] @
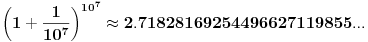
Probaj za 10^n , n>100
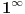 jedan kao broj 1. Onda jeste sve to =1.
Ali ako jedna stvar teži kecu, a u isto vreme se to "diže" na beskonacno onda može da bude šta god hoćeš.
Pa se zato kaže da je neodređeno.
U našem "e slučaju" 1+0>1 to je poenta. [ SrdjanR271 @ 21.04.2011. 19:02 ] @
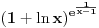
Ovo je direktnom zamenom x=1+ isto 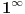
A ustvari je

Može i ovaj
 [Ovu poruku je menjao SrdjanR271 dana 21.04.2011. u 20:48 GMT+1]
[Ovu poruku je menjao SrdjanR271 dana 21.04.2011. u 20:48 GMT+1][ atelago @ 21.04.2011. 20:09 ] @
Ako važi binomni obrazac i kada je jedan od članova jednak nuli onda nije jasno
zašto su članovi tipa
k n1 ∞ - n0 n
kojih ima beskonačno mnogo izjednačeni sa nulom kad se vidi da su svi oni proizvodi
od beskonačno i nule što je takođe nedefinisano?
Od beskonačno mnogo članova uzet je samo prvi t.j. 1 ∞. Zašto?
Citat: Ali ako jedna stvar teži kecu, a u isto vreme se to "diže" na beskonacno onda
može da bude šta god hoćeš. Pa se zato kaže da je neodređeno.
Ne bi trebalo da je tako jer se uvek zna koja je to stvar i kako teži ka kecu.
Citat: U našem "e slučaju" 1+0>1 to je poenta.
Ako je tako onda je 1/∞ > 0 odnosno 1/∞ nije nula, ali Nedeljko kaže da jeste. [ SrdjanR271 @ 21.04.2011. 20:48 ] @
1/∞ teŽi nuli
[ kandorus @ 21.04.2011. 22:40 ] @

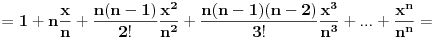
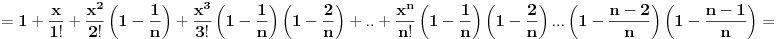
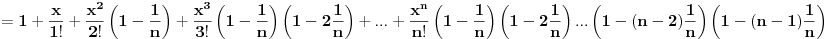
Ako se uzme da je (1/n)==0, tada
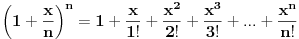
Ako je x=0 tada je zbir sa desne strane = 1, kao da se u zagradama stepenuje jedinica.
Ako je x>0 tada je zbir sa desne strane > 1, u zagradama se stepenuje izraz > 1.
Ako je x < 0 tada je zbir sa desne strane manji od 1, u zagradama se stepenuje izraz < 1.
2:1 za one koji tvrde da je rezultat različit od 1. :) [ Nedeljko @ 22.04.2011. 01:26 ] @
@atelago
Savetujem ti da naučiš realne brojeve.
Citat: kandorus:Ako se uzme da je (1/n)==0, tada
Xa, xa, xa! [ kandorus @ 22.04.2011. 06:34 ] @
Šta, ne verujete? Probajte:
Code:
#include <math.h>
void main( void )
{
double n = 1.7E308;
double y;
y = pow( 1+1/n, n );
printf( "\%lf", y );
}
Dobićete čistu jedinicu! [ SrdjanR271 @ 22.04.2011. 12:09 ] @
Da dobicemo, ali to nije matematika.
Matematika se ne dokazuje programiranjem.
[ kandorus @ 22.04.2011. 13:18 ] @
Prvo, ne dokazujem ništa. Samo sam pokazao kako neko rezonuje. Na primer tvorci C-a.
Drugo, mislim da su računari korišćeni pri dokazivanju nekih teorema i to nedavno, ali sad ne mogu tačno da citiram o čemu je reč.
[ Nedeljko @ 22.04.2011. 14:04 ] @
To samo pokazuje nesavršenost pokretnog zareza i to nema veze sa C-om, već sa fundamentalnom nemogućnošću da se u računaru predstavi svih beskonačno mnogo decimala realnog broja. U ovom slučaju je u principu bilo moguće koristiti tačno predstavljanje racionalnih brojeva (u obliku para brojilac, imenilac), ali bi bilo nepraktično jer bi brojilac i imenilac zahtevali veliki (mada konačan) memorijski prostor kakav je bar u nekoj doglednoj budućnosti neostvariv.
Računari se zaista koriste za dokazivanje teorema, ali ne tako kako si zamislio. Jedan od najstarijih ozbiljnih primera je problem četiri boje. Dokazana je teoreme po kojoj se svaki planaran graf može obojiti u četiri boje. Ljudi su najpre dokazali da se opšti slučaj svodi na izvestan konačan podslučaj. Naime, ako je svaki graf iz tačno određenog konačnog skupa planarnih grafova može obojiti sa četiri boje, onda se svaki planaran graf može obojiti u četiri boje. Zadatak računara je bio da grafove iz tog konačnog skupa oboji u četiri boje.
Naravno, upotreba računara je na tom polju odmakla mnogo od onda.
[ SrdjanR271 @ 22.04.2011. 14:05 ] @
Citat: kandorus: Prvo, ne dokazujem ništa. Samo sam pokazao kako neko rezonuje. Na primer tvorci C-a.
Drugo, mislim da su računari korišćeni pri dokazivanju nekih teorema i to nedavno, ali sad ne mogu tačno da citiram o čemu je reč.
Znam da se računari koriste i za nalaženje nula zeta f-je, i za dokazivanje (npr. Four color theorem). Ali to sa C-om je drugo.
Računari korišćeni pri dokazivanju nekih teorema koriste "dobre" algoritme.
pow je "dobar" ali ne zna limese, što nije njegov posao. [ edisnp @ 22.04.2011. 14:23 ] @
Culi ste svi za Dijsktrin algoritam za nalazenje najkraceg puta koji se
razvija i programiranje i matematickim putem preko nekakvih grafova.
[ kandorus @ 22.04.2011. 14:32 ] @
Citat: ^Nedeljko
ali ne tako kako si zamislio.
Šta sam zamislio?
Citat: ^SrdjanR271
pow je "dobar" ali ne zna limese
Pa sad, kako da ti kažem, taj c-program što sam napisao je samo računanje stepena a ne limesa. U stvari u celoj ovoj temi do sada nisam pomenuo limes.
Osim toga, forumule koje sam izveo treba da pokažu zašto se binom
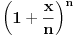
ne može svesti na 1 čak i za velike vrednosti n jer je dobijen izraz koji samo u specijalnom slučaju x=0 postiže vrednost 1.
Umesto da se diskusija širi u nepotrebnom smeru mogao bi neko da ospori izvodjenje ako može ili da pokaže na drugi način.
[Ovu poruku je menjao kandorus dana 22.04.2011. u 16:36 GMT+1][ SrdjanR271 @ 22.04.2011. 15:07 ] @
Citat: edisnp: Culi ste svi za Dijsktrin algoritam za nalazenje najkraceg puta koji se
razvija i programiranje i matematickim putem preko nekakvih grafova.
Jesmo. I šta sa njim? [ Nedeljko @ 22.04.2011. 16:54 ] @
Ni pow nije "dobar", jer pravi računsku grešku.
Pa, pomenuo si taj program i dokazivanje teorema pomoću računara. U tom dokazivanju se ne koriste "grešne" stvari kao što je FPU, osim kada je ta greška pod kontrolom.
Citat: kandorus: Osim toga, forumule koje sam izveo treba da pokažu zašto se binom
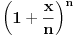
ne može svesti na 1 čak i za velike vrednosti n jer je dobijen izraz koji samo u specijalnom slučaju x=0 postiže vrednost 1.
Binom ima vrednost 1 i za 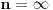 . Za konačne vrednosti  i 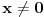 ne. Naravno, u prvom slučaju je beskonačan stepen jedinice nedefinisan. [ atelago @ 22.04.2011. 19:08 ] @
Nedeljko:
Citat: Savetujem ti da naučiš realne brojeve.
Hvala na savetu! Potrudiću se. U međuvremenu ću se poslužiti tvojim iskustvom iznetim ovde.
Nadam se da nemaš ništa protiv.U jednoj poruci napisao si ovo:
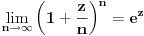 za svako 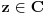
(Ova formula je baš zgodna za dokazivanje koliko je 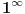 i koliko je 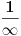 )
Neka je z = 0. Budimo malo i formalisti pa to i napišimo:
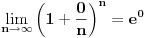
Vrednost u zagradi je, prema tome, jednaka 1 i ta vrednost se beskonačno puta množi sama sa sobom
i dobijamo da je rezultat jednak 1 zato što je 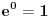
Zar može biti jednostavniji dokaz?
Međutim, ako ako umesto z = 0 stavimo da je z = 1 onda dobijamo 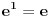 , a broj e nije
jednak 1 nego 2,71828… Odakle sad ta razlika od 1,71828… kad je po tvom iskustvu 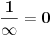
pa se ni u zagradi ni nad zagradom ništa nije promenilo ?
Stvar je potpuno jasna – 1/∞ se ne može poistovećivati sa nulom već je to beskonačno mala vrednost za koju
je izraz u zagradi veći od 1 i kad se taj izraz beskonačno puta pomnoži sa sobom dobija se broj e.
To takođe znači da je 1/∞ ≠ 2/∞ ≠ 3/∞ ≠ 5/∞ i t. d. Ako ne veruješ uveri se jer se po gornjoj
formuli dobijaju limesi 1, e, e 2, e 3, e 5
Dakle, ako je jedinica sama onda je 1∞ = 1, a ako nije sama onda rezultat zavisi od «društva» i
samo zbog tog društva kaže se da je 1 ∞ nedefinisano jer rezultat od njega zavisi tako kako je pokazano
i kako još može biti. [ Nedeljko @ 22.04.2011. 20:11 ] @
Citat: atelago: Hvala na savetu! Potrudiću se.
Pa, potrudi se. Ovako ne možemo da raspravljamo, jer ne poseduješ elementarna potrebna znanja. Nabavi bilo koji užbenik matematičke analize 1 za matematički fakultet. Tamo ćeš naći aksiome polja realnih brojeva, definiciju limesa, metode računanja itd.
Za početak, u polju realnih brojeva ne postoje beskonačno male veličine, a u proširenom skupu realnih brojeva je  jedna jedina konstanta, tj. nema razli;itih beskona;nosti. [ kandorus @ 22.04.2011. 23:17 ] @
Citat: atelago
To takođe znači da je 1/∞ ≠ 2/∞ ≠ 3/∞ ≠ 5/∞ i t. d. Ako ne veruješ uveri se jer se po gornjoj
formuli dobijaju limesi 1, e, e2, e3, e5
2/∞ = 2/(2*∞) = 1/∞ = 0
Budući da je limes proizvoda jednak proizvodu limesa dobija se:
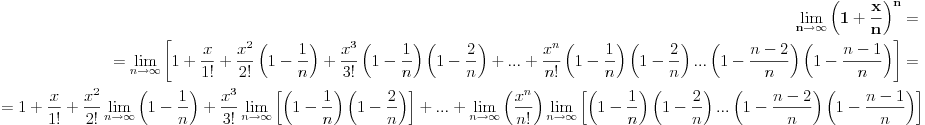
Iz poslednjeg izraza može se uočiti da su članovi (1-1/n), (1-2/n), ..., (1-(n-2)/n), (1-(n-1)/n) uvek prisutni bez obzira kolika je vrednost x. Vrednost stepena broja e odredjuje član x k/k!. Zato što, za male vrednosti k proizvod (1-1/n)(1-2/n), ..., (1-(k-1)/n) teži 1 a kad k->∞ tada proizvod (1-1/n)(1-2/n), ..., (1-(k-1)/n) teži 0 jer i n->∞. [ Nedeljko @ 23.04.2011. 00:20 ] @
Citat: kandorus: Budući da je limes proizvoda jednak proizvodu limesa
Samo ako imaš fiksan konačan broj činilaca, tj. za svako 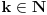 važi: Ako su  konvergentni nizovi, onda je niz  konvergentan i tačna je jednakost
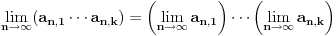 .
No, u načem slučaju je broj činilaca promenljiv i teži beskonačnosti. [ kandorus @ 23.04.2011. 07:47 ] @
Samo što taj beskonačni proizvod nije razlagan!
Obrati pažnju, razlaganje je izvršeno na dva člana!
[ Nedeljko @ 23.04.2011. 09:07 ] @
Jao, tek sad vidim šta si napisao. U poslednjem redu ti se pojavljuje n van limesa. To tek nema smisla.
Treba ti nešto ovako:
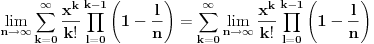 .
To važi pod uslovom da je
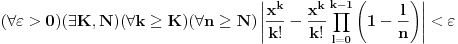
za svako  , što je svakako ispunjeno. [ kandorus @ 23.04.2011. 10:12 ] @
Gde se "pojavljuje n van limesa"?
[ Nedeljko @ 23.04.2011. 10:54 ] @
Opet nisam dobro video. Ne pojavljuje se van limesa, ali ne vidim da poslednji red ima smisla. Koliko imaš sabiraka u poslednjem redu? Obzirom da si napisao
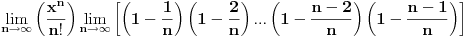
kao poslednji sabirak, reklo bi se da sabiraka ima konačno mnogo, ali nije jasno koliko. [ kandorus @ 23.04.2011. 11:35 ] @
Pa dodaću tri tačke i ako uvedem opšti k-ti član uz prelom reda onda je pogodnije za pregled:
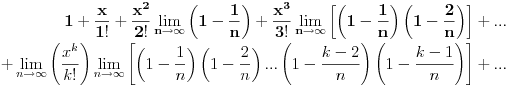 [ Nedeljko @ 23.04.2011. 11:54 ] @
Bezveze je što je 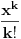 pod limesom, a 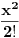 nije, pa zbunjuje, mada je to naravno isto.
Dakle, pikiraš na
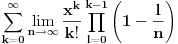 ,
a imao si
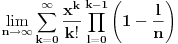 .
Za tu razmenu mesta limesa i sume ti treba onaj uslov koji sam napisao i koji je svakako ispunjen. [ atelago @ 23.04.2011. 12:20 ] @
Nedeljko:
Citat: Ovako ne možemo da raspravljamo, jer ne poseduješ elementarna potrebna znanja.
Znanja, pogotovu elementarna su svakako potrebna, ali su beskorisna ukoliko ne posedujemo
elementarnu moć rasuđivanja. Na primer nije bitno da li u polju realnih brojeva postoje
infinitezimale ili ne, ako nam one u konkretnom slučaju služe da rešimo neki problem. Kad
integrališ neku površinu onda je elementarna površina dF = f(x)dx. Koliki je diferencijal dx?
Koliko takvih diferencijala može stati na 1 cm dužine apscise? Stvarno ne razumem šta si
hteo da kažeš.
Drugo: Mislim da nigde nisam govorio o različitim beskonačnostima.
Treće: Ne govoriš o problemu odnosno o temi. Budi ljubazan pa mi kaži gde si našao greške
u mojoj prethodnoj poruci i saopšti ih. Bilo bi fer.To treba činiti u dobroj nameri.
Kandorus:
Citat: 2/∞ = 2/(2*∞) = 1/∞ = 0
Prihvatam šalu i dodajem: nije 2/∞ jednako 1/∞ nego 4/∞. Evo pogledaj 2/∞ = 2/(0,5*∞) = 4/∞.
Ovo je bila šala, ali ovo nije šala nego greška:
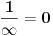
jer nije u saglasnosti s ovim:
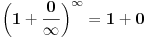
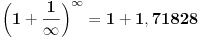
Sta je uzrokovalo drukčiji rezultat u drugoj jednačini?
Ovo su dva realna broja koja postoje nezavisno od toga da li su limesi nekih nizova ili nisu.
Pogrešno je reći «broj e je limes». Broj e je realan broj kao i ostali realni brojevi i on može
biti limes niza kao što i ostali realni brojevi mogu biti limesi nekih nizova. Broj e ne teži nikuda
on je konstanta koja se ne dobija kada «n teži ka beskonačno» nego kada n jeste beskonačno.
Težnja se odnosi na članove niza koji mu se približavaju a ne na njega, a on, konkretno,
čak i nije član toga niza. [ Bojan Basic @ 23.04.2011. 15:56 ] @
Atelago, mogu li samo priupitati šta je O u tvom imenu? Da li, kad se čita unatrag, stoji kao prvo slovo od osveta galeta, ili si neku drugu reč imao u vidu?
[ SrdjanR271 @ 23.04.2011. 16:45 ] @
Citat: Bojan Basic: Atelago, mogu li samo priupitati šta je O u tvom imenu? Da li, kad se čita unatrag, stoji kao prvo slovo od osveta galeta, ili si neku drugu reč imao u vidu?
Bravo. I da nije galet, svaka čast za zapažanje. Ne bi mi nikad palo na pamet. [ Nedeljko @ 23.04.2011. 17:21 ] @
I ja sam pomislio da je galet, ali me je pokolebao kada je na trenutak rekao da je voljan da uči! No, poslednjom porukom se razotkrio, pa mu nisam odgovarao.
[ kandorus @ 23.04.2011. 19:45 ] @
Citat: atelago
Ovo je bila šala, ali ovo nije šala nego greška:
1/∞ = 0
jer nije u saglasnosti s ovim:
(1 + 0/∞)∞ = 1 + 0
(1 + 1/∞)∞ = 1 + 1.71828
Sta je uzrokovalo drukčiji rezultat u drugoj jednačini?
Kad se uključi simbol ∞ onda taj izraz ne znači da se množenje i deljenje vrši kao u osnovnoj školi (n binoma se pomnoži) već se moraju uzeti u obzir pravila koja važe za granične vrednosti. Transformacijom izraza pre prelaska na granične procese vidi se zašto se dobijaju različiti rezultati. Upravo zato sam izdvojio opšti član:
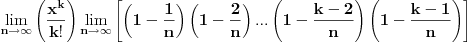
Ono što posebno odreduje vrednost stepena (e x) je član x k/k!.
Iz datog izraza se vidi da je promenljiva x (kojom se stepenuje e) izdvojena iz limesa proizvoda. Unutar limesa proizvoda se javljaju konstante nezavisne od x. Konstante su iz skupa {1, 2, ..., k-1} i iste su za svako x. Zato je vrednost limesa proizvioda ista za odgovarajući član sabirka i nezavisna od vrednosti promenljive x.
Nakon tih transformacija može da se predje na granični proces te se za opšti član sume dobija vrednost
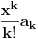
gde je 0 < a k < 1. Još jednom, a k ne zavisi od x. [ atelago @ 16.07.2011. 20:40 ] @
Citat: Bojan Basic:
Atelago, mogu li samo priupitati šta je O u tvom imenu?
Možeš! Upravo si to i učinio. U mom imenu nema slova O.
Citat: Da li, kad se čita unatrag, stoji kao prvo slovo od osveta galeta, ili si neku drugu reč imao u vidu?
Zašto bih ja osvećivao galeta? Da li sam mojim porukama nekom naneo zlo koje liči na osvetu?
Nekada sam živeo u Babinu Potoku pored Plitvica. Otuda i potiče "ate lago".
Pošto sam poistovećen sa galetom neko vreme nisam imao pristup ovde, pa nisam mogao da
odgovorim, slučajno sam otkrio da mogu da se ulogujem i to sada koristim ukoliko me sličnost sa
galetom ne diskvalifikuje. [ Nedeljko @ 17.07.2011. 09:48 ] @
Citat: atelago: Nekada sam živeo u Babinu Potoku pored Plitvica. Otuda i potiče "ate lago".
Pa, dobro, i galet je mogao da živi tamo. Stavovi su ti vrlo slični galetovim. [ SrdjanR271 @ 17.07.2011. 10:20 ] @
Citat: atelago:
Nekada sam živeo u Babinu Potoku pored Plitvica. Otuda i potiče "ate lago".
A jel "ate" znači baba, pošto je valjda "lago" na španskom jezero?
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|