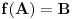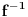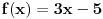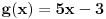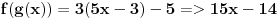|
|
[ demicM @ 15.04.2011. 14:55 ] @
|
| Pozdrav!
Oduvek sam imao problem da shvatim suštinu funkcije. Zapravo, u literaturi uvek sam se susretao sa različitim objašnjenjima koja su drugačija
Mene buni nekoliko stvari što se tiče funkcije.
Funkcija (kako sam učio u školi) je: preslikavanje svakog elementa skupa A sa tačno jednim elementom skupa B
Da li je ovo dobra definicija?
Dalje se kaže: kada se radi o preslikavanju a ne samo o relaciji kažemo da FUNKCIJA f PRIDRUŽUJE ELEMENTU X ELEMENT Y ILI DA f PRESLIKAVA X u Y
E sad, šta me buni ovde
1. Zar nije preslikavanje zavisno od relacije, kako se onda razdvajaju ova dva pojma ovde ?
2. Ako se element X iz skupa A preslikava u element Y skupa B, o kakvom PRIDRUŽIVANJU SE OVDE GOVORI???? Kakvo je to PRIDRUŽIVANJE ELEMENTA Y ELEMENTU X ???? Zapravo koja je razlika između PRESLIKAVANJA I PRIDRUŽIVANJA???? Ako se X preslika u Y, kako to da se Y pridruzi iksu???
Pojasnite mi ove funkcije jer nikad nisam mogao da ih razumem. Uvek sam ih zbog toga učio napamet i imao problema da shvatim daljnje gradivo iz matematike. Hvala!
EDIT:
pogledajte različite definicije funkcije koje me takođe bune, jer su neke kontradiktorne:
1. Iz udžbenika: u gornjem postu sam napisao
2. Iz jedne skripte: Funkcija je preslikavanje skupova. Imamo 2 neprazna skupa A i B. Pravilo ili propis po kojemu svakom elementu skupa A dodjeljujemo točno jedan element skupa B zove se funkcija. Kažemo da se skup A preslikava u skup B A->B ili f: A->B .
3. Sa wiki: Funkcija je, uopšte, pravilo pridruživanja jednog elementa iz skupa H (domen funkcije) drugom iz skupa U (kodomen funkcije).
4. Iz sveske (profesoricina) Funkcija A --> B je svako pridruživanje elemenata skupa A elementima skupa B, za koje vredi ono pravolo da za svako x iz skupa A postoji jedno y u skupu B.
5. Iz jedne druge skripte: Neka su D i K dva neprazna skupa. Preslikavanje koje svakom elementu skupa D pridružuje tačno jedan element skupa K zove se funkcija sa D u K, oznaka
f : D → K. |
[ SrdjanR271 @ 15.04.2011. 15:14 ] @
Kod funkcija, kao i kod relacija, uspostavlja se veza između elemenata dva skupa,
ali dok kod relacija jednom elementu x skupa A mogu odgovarati više elemenata skupa B,
kod funkcija jednom elementu x skupa A može odgovarati samo jedan elemenat y skupa B.
[ demicM @ 15.04.2011. 17:08 ] @
Srdjane, nije to problem nego ovo boldovano:
Kada se radi o preslikavanju, a ne samo o relaciji, onda umesto (x,y E f) pišemo y=f(x) i kažemo da funkcija f pridružuje elementu x element y ili da preslikava x u y.
Koja je razlika između preslikavanja x u y i pridruživanja y u x?
[ SrdjanR271 @ 15.04.2011. 17:16 ] @
Funkcija ili preslikavanje.
A kako bi ti rekao šta f-ja "radi" elementu x, nego pridružuje y.
[ demicM @ 15.04.2011. 17:23 ] @
zar ona ne preslikava element x iz skupa A u y skup B??
[ lonelyrider_44 @ 15.04.2011. 17:40 ] @
Vrtiš se oko jednog te istog. Za neko x iz skupa A, postoji y u skupu B. Znači postoji par (x,y) . Možeš reći da funkcija preslikava x u y, ili da x-u pridružuje y.
[ demicM @ 15.04.2011. 17:48 ] @
Citat: lonelyrider_44:
Vrtiš se oko jednog te istog. Za neko x iz skupa A, postoji y u skupu B. Znači postoji par (x,y) . Možeš reći da funkcija preslikava x u y, ili da x-u pridružuje y.
Ma jasno je to meni, nego nije mi jasno zašto se BAŠ kaže da se x-u pridružuje y... zašto se ne kaže da se ipsilonu pridruži iks, ili pak da funkcija uparuje x i y? meni je tako logičnije [ lonelyrider_44 @ 15.04.2011. 17:58 ] @
Ali baš nije logično. y se računa NA OSNOVU x vrednosti. y je zavisna promenljiva, jer zavisi od x-a pa se zato x-u pridružuje y, a ne y-u x, jer se kreće od x-a, a ne y-a.
[ demicM @ 15.04.2011. 18:05 ] @
hvala puno na odgovorima
da sumiramo... y se pridruzuje iksu iako se iks preslikava u y?
[ markob15 @ 16.04.2011. 05:28 ] @
Citat: demicM: Ma jasno je to meni, nego nije mi jasno zašto se BAŠ kaže da se x-u pridružuje y... zašto se ne kaže da se ipsilonu pridruži iks, ili pak da funkcija uparuje x i y? meni je tako logičnije
Da, y se pridruzuje x-u kada funkcija preslikava x u y.
Nemoj da te to buni, samo je terminologija u pitanju, sinonimi su:
x se slika u y
x se preslikava y
x-u odgovara y
x-u je PRIDRUZEN y
Dakle, kao sto je rekao lonelyrider_44, kada su funkcije u pitanju y ZAVISI OD x a ne obrnuto.
Npr. ako imas funkciju f(x) = 5x+2, (ili y = 5x+2 svejedno je)
za x =1 bice f(x)=7
za x =0 bice f(x)=2
za x = 1/5 bice f(x)=3 itd...
odnosno svakom elementu x pridruzuje se vrednost funkcije koja zavisi od tog iks-a,
ondnosno ipsilon zavisi od iks-a, t.j. ipsilon menja svoju vrednost u odnosu na promenu iks-a (ako je x=1 bice y=7, x=0 bice y=5...)
rec "pridruzivanje" samo je stvar terminologije, gledaj na to kao sto se zbiru brojeva 4 i 5 "pridruzuje" njihov zbir (odnosno broj 9), ili kao sto se nekoj jednacini pridruzuje njeno resenje...takav vid pridruzivanja...to je samo nacin da se kaze da su x i y u nekoj VEZI, nista vise..
tacno je da fukcija uparuje x i y, ali oni nisu "ravnopravni" (jer y zavisi od x) [ demicM @ 16.04.2011. 09:53 ] @
Citat: Da, y se pridruzuje x-u kada funkcija preslikava x u y.
Nemoj da te to buni, samo je terminologija u pitanju, sinonimi su:
x se slika u y
x se preslikava y
x-u odgovara y
x-u je PRIDRUZEN y
Dakle, kao sto je rekao lonelyrider_44, kada su funkcije u pitanju y ZAVISI OD x a ne obrnuto.
Npr. ako imas funkciju f(x) = 5x+2, (ili y = 5x+2 svejedno je)
za x =1 bice f(x)=7
za x =0 bice f(x)=2
za x = 1/5 bice f(x)=3 itd...
odnosno svakom elementu x pridruzuje se vrednost funkcije koja zavisi od tog iks-a,
ondnosno ipsilon zavisi od iks-a, t.j. ipsilon menja svoju vrednost u odnosu na promenu iks-a (ako je x=1 bice y=7, x=0 bice y=5...)
rec "pridruzivanje" samo je stvar terminologije, gledaj na to kao sto se zbiru brojeva 4 i 5 "pridruzuje" njihov zbir (odnosno broj 9), ili kao sto se nekoj jednacini pridruzuje njeno resenje...takav vid pridruzivanja...to je samo nacin da se kaze da su x i y u nekoj VEZI, nista vise..
tacno je da fukcija uparuje x i y, ali oni nisu "ravnopravni" (jer y zavisi od x)
Nije mi jasno jer izgleda imam pogrešnu percepciju šta je funkcija...

Zar nije f(a)=alfa?
Zar se ne preslikava element >a< iz DOMENA u element alfa u KODOMENU???
Zar se ovo ne čita: >a< se preslikava u >alfa<??? Ako da, šta se podrazumeva pod tim da se >a< preslikava u >alfa<? Šta je onda to PRESLIKAVATI? Ja sam mislio da preslikavati >a< u >alfa< znači da >alfa< ima vrednost koju je imala + vrednost >a<. Tako mi jezički logično zvuči da znači reč preslikati... Kao kad uzmeš poster pa ga preslikaš na papir.
f(a)=alfa - da li se u ovom slučaju >a< posle preslikavanja nalazi u skupu B, tj. da li se ta "preslikanost" nalazi u skupu B (šta se onda zbiva sa alfom), a originalu >a< dodaje vrednost alfa (šta se onda zbiva sa >a<)????
Ako vam nije mrsko, pojasnite mi funkciju ispočetka detaljnije. Upetljao sam se kao pile u kučine... ni sam više ne znam šta hoću da kažem....
[Ovu poruku je menjao demicM dana 16.04.2011. u 11:04 GMT+1]
[Ovu poruku je menjao demicM dana 16.04.2011. u 11:10 GMT+1]
[Ovu poruku je menjao demicM dana 16.04.2011. u 11:12 GMT+1]
[Ovu poruku je menjao demicM dana 16.04.2011. u 11:15 GMT+1]
[Ovu poruku je menjao demicM dana 16.04.2011. u 14:30 GMT+1][ demicM @ 16.04.2011. 10:30 ] @
Razlika između preslikavati i pridružiti je, ako sam dobro shvatio, u sledećem:
1. f(a)=alfa
Preslikavati
>a< ulazi u skup B i preslikava se u >alfa< (šta se onda zbiva sa alfom?)
2. f(a)=alfa
Pridružiti
alfa ulazi u skup A i pridružuje se vrednosti >a< (šta se onda zbiva sa a?)
Da li je to to?
Ja znam da je funkcija >a< ---> >alfa< zapravo skup koji se sastoji iz >a< i >alfa< - da li to saznanje trebam da koristim da bih shvatio funkciju?
Citat: Npr. ako imas funkciju f(x) = 5x+2, (ili y = 5x+2 svejedno je)
za x =1 bice f(x)=7
odnosno svakom elementu x pridruzuje se vrednost funkcije koja zavisi od tog iks-a,
ondnosno ipsilon zavisi od iks-a, t.j. ipsilon menja svoju vrednost u odnosu na promenu iks-a (ako je x=1 bice y=7)
F(x) = 5*1+2, F(x) = 7, y u slučaju f(x) je 7. Dakle y=7. Dobro.
Mene sad zanima i to koliko je y BEZ funkcije f(x). Da li je y = 2?
[Ovu poruku je menjao demicM dana 16.04.2011. u 11:45 GMT+1]
[ SrdjanR271 @ 16.04.2011. 12:13 ] @
Citat: Mene sad zanima i to koliko je y BEZ funkcije f(x). Da li je y = 2?
ako je y=2, možeš reći y(x)=2, ili f(t)=2, g(x)=2 ...... [ demicM @ 16.04.2011. 12:38 ] @
Citat: ako je y=2, možeš reći y(x)=2, ili f(t)=2, g(x)=2 ......
Hvala na odgovoru, ali nisam to pitao. Možda se nisam dobro izrazio pa si pogrešno razumeo.
Ja sam pitao koliko je y iz njegovog primera. Pri tome mislio sam na y bez funkcije f(x). F(x) = 7, dakle y = 7 - - - ali ja nisam to pitao, već se moje pitanje odnosi na vrednost y iz njegovog primera u slučaju da nema funkcije f(x). [ SrdjanR271 @ 16.04.2011. 12:52 ] @
Jel ovaj primer y=5x+2?
Ako da, onda je isto
y(x)= 5x+2 ili y(t)= 5t+2, ili f(x)= 5x+2 ili s(p)= 5p+2 ...
Pitanje koliko je y BEZ funkcije f(x) nema smisla.
Ono što je on napisao
za x=1, f(x)=5*1+2 nije ok jer treba ovako f(1)=5*1+2=7.
Možda te je to bunilo.
[ demicM @ 16.04.2011. 13:12 ] @
Citat: Jel ovaj primer y=5x+2?
Ako da, onda je isto
y(x)= 5x+2 ili y(t)= 5t+2, ili f(x)= 5x+2 ili s(p)= 5p+2 ...
Hvala na odgovoru, ali nisam to pitao...
Citat:
Ono što je on napisao
za x=1, f(x)=5*1+2 nije ok jer treba ovako f(1)=5*1+2=7.
Možda te je to bunilo.
Nije me to bunilo :). Znam to.
Citat: Pitanje koliko je y BEZ funkcije f(x) nema smisla.
otprilike nešto ovako sam pitao, mada ne verujem da se baš razumemo (mojom krivicom). vratiću se ponovo na to pitanje koje mi sada i nije toliko važno kao druga pitanja koja sam postavio u gornjim postovima (11 i 12 post na ovoj temi). Na ta pitanja bih voleo da dobijem odgovor kako bih shvatio funkciju(e).
[ lonelyrider_44 @ 16.04.2011. 13:18 ] @
Citat: demicM:
F(x) = 5*1+2, F(x) = 7, y u slučaju f(x) je 7. Dakle y=7. Dobro.
Mene sad zanima i to koliko je y BEZ funkcije f(x). Da li je y = 2?
[Ovu poruku je menjao demicM dana 16.04.2011. u 11:45 GMT+1]
F(1)=5*1+2
F(1)=7
(x,y)=(1,7)
isto tako,
F(0)=5*0+2
F(0)=2
ili
y=2
(x,y)=(0,2)
E sad, nije mi baš najjasnije na šta si ciljao kad si pitao koliko je y BEZ f-je f(x). Ako nema f-je f(x), onda se gubi pravilo preslikavanja (5*x+2), nema ga, jer to je f(x).
A y je 2, samo ako je x = 0, na osnovu f(x).
Nisam siguran šta je tačno ono što te zbunjuje, ne obraćaj toliko pažnje na terminologiju. Jednostavno, par (x,y) prema nekoj f-ji f(x) mora da bude takav da x i y zadovoljavaju jednakost definisanu tom funkcijom.
U ovom konkretnom primeru, (x,y) mora da zadovoljava f-ju y = 5x+2 .
Pomenuto je već da se y računa na osnovu x-a, ali može i obrnuto. Što znači, ako uzmeš da je y = 2, onda treba odrediti x.
2 = 5 * x + 2
Ako NEMA f(x), onda nema ni y-a, zar ne? Jer, y = f(x) = 5x+2 (u ovom konkretnom slučaju) , tj. tada je y obična promenljiva koja može da ima bilo koju vrednost, i nema nikakve povezanosti sa x-om.
Znači, uređen par (0,2) pripada f-ji, a recimo (0,7) ne pripada datoj f-ji.
[ demicM @ 16.04.2011. 15:48 ] @
Hvala vam što se trudite da mi objasnite
Vratimo se na preslikavanje i pridruživanje, molim vas!!! Odgovorite mi na 11-ti i 12-ti post
Samo bih još nešto dodao što se tiče 11-tog i 12-tog posta
http://upload.wikimedia.org/wikipedia/sr/3/3d/Funkcija.gif
Funkcija (a) = alfa, f(a)=alfa
E sad,
ovo znači da se >a< PRESLIKAVA iz domena A u kodomen B (u element >alfa<) - Je li tako???
onda se kaže da se element >alfa< iz kodomena PRIDRUŽUJE elementu >a< u DOMEN - Je li tako??????
Ako je tako, kako je moguće da se >alfa< pridruži nečemu što se već preslikalo u njega samo (element >a<)???
Da li to znači da skup A sadrži i >alfu<? Da li to znači da skup B sadrži >a<???, odnosno da je ta relacija funkcija
Koja je suštinska razlika i koja su svojstva PRESLIKAVANJA i PRIDRUŽIVANJA????? Molim vas da mi to pojasnite.
(vidi 11-ti i 12-ti post)
možda sam debil, ali stvarno ne razumem. ili sam pogrešio negde u startu ili sam nešto zanemario...
hvala [ markob15 @ 16.04.2011. 20:26 ] @
11. post:
Citat: Zar nije f(a)=alfa?
Zar se ne preslikava element >a< iz DOMENA u element alfa u KODOMENU???
Da preslikava se. Samo tvoje tumacenje pojma "preslikavati" nije ispravno.
Citat: Ja sam mislio da preslikavati >a< u >alfa< znači da >alfa< ima vrednost koju je imala + vrednost >a<.
NE
Citat: f(a)=alfa - da li se u ovom slučaju >a< posle preslikavanja nalazi u skupu B,
NE
Citat: tj. da li se ta "preslikanost" nalazi u skupu B (šta se onda zbiva sa alfom), a originalu >a< dodaje vrednost alfa (šta se onda zbiva sa >a<)????
Vidis ako se >a< iz domena preslikava u >alfa< iz kodomena, to NE ZNACI da je >a< proshetao iz domena i infiltrirao se medju redove elemenata kodomena i postao >alfa<
element >a< nije mrdnuo iz svog skupa (t.j. domena) kao sto ni >alfa< nije nigde utekao.
Rec preslikavanje samo oznacava da su elementi a i alfa u nekoj vezi, odnosno elementu >a< iz domena odgovara element >alfa< iz kodomena.
Mozda je jednostavnije te osnove shvatiti na nekom "zivotnijem primeru", evo jednog:
Npr. imas neki fudbalski tim, i trebas svakom igracu da dodelis dres sa odgovarajucim brojem.
Dakle imas skup igraca (domen) i skup brojeva (kodomen),
e sad jedan igrac zeli da nosi dres sa brojem 5, drugi hoce 10 itd..
Dakle, ti svakom igracu (t.j. element >a< iz domena) dodelis, t.j. pridruzis mu odgovarajuci broj (po njegovoj zelji i pod uslovom da je broj slobodan naravno) odnosno element >alfa< iz kodomena.
Kao sto vidis niti je igrac (t.j. >a<) postao broj (t.j. >alfa<) niti je broj postao igrac, jednostavno su se povezali, sada kada komentator kaze: "igrac sa brojem 15" ti tacno znas o kom je igracu rec i obrnuto.
Moras da shvatis jedno: preslikavanje = pridruzivanje, to su sinonimi ,samo je nekad zgodnije reci "preslikavanje" a nekad "pridruzivanje" (kao sto sam ja koristio u predhodnom primeru)
Dakle funkcija je pre svega zakon (pravilo) pomocu kog svakom elementu domena pridruzis njemu odgovarajuci (u odnosu na taj zakon) element kodomena.
Prilikom preslikavanja ( pridruzivanja) nista se ne dogadja sa polaznim skupovima, samo se definise veza izmedju njih.
E sad, ako ta veza svaki element domena poveze (pridruzi, preslika) sa samo jednim elementom kodomena, onda se ta veza naziva funkcija.
Npr. ovakve veze JESU funkcije:
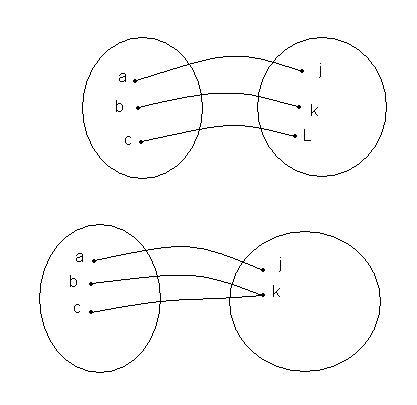
ovakve NISU:
 [Ovu poruku je menjao markob15 dana 16.04.2011. u 22:04 GMT+1]
[Ovu poruku je menjao markob15 dana 16.04.2011. u 22:04 GMT+1][ markob15 @ 16.04.2011. 21:37 ] @
12. post:
Citat: Mene sad zanima i to koliko je y BEZ funkcije f(x). Da li je y = 2?
Ne.
Kao sto rekoh, funkcija je pravilo po kojem dovodimo u vezu elemente domena sa elementima iz kodomena.
U ovom primeru to pravilo glasi: "na osnovu izabranog x-a t.j. elementa domena, nadji takav element y iz kodomena koji odgovara formuli f(x)=5x+2"
t.j. "nadji takav y da je jednak broju dobijenom kada se x pomnozi sa 5 i doda mu se 2".
ta funkcija graficki izgleda ovako:
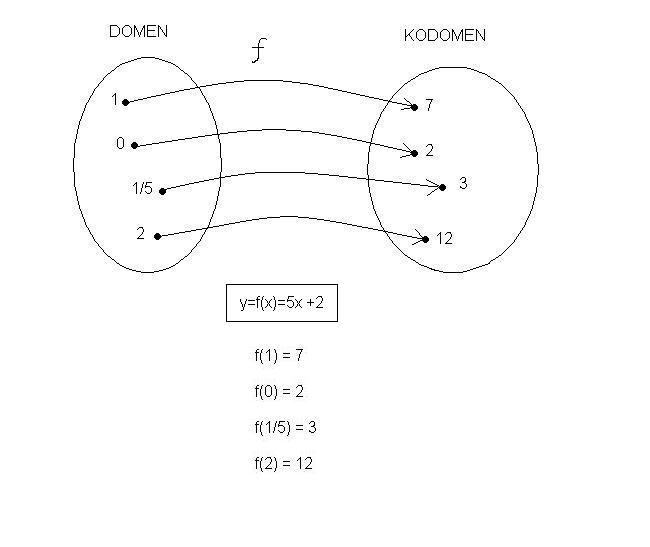
Pitanje koliko je y bez funkcije f(x) nema smisla.
Zapis f(x) znaci "primeni pravilo f na element x". Kada se to pravilo primeni, dobije se elemet y. Dakle y=f(x).
Evo jos jednog primera:
f(x)=5
to znaci da se svi elementi x "slikaju" u broj 5.
x=1 sledi y =5
x=2 sledi y =5
x=3 sledi y =5
to je takodje funkcija, jer svaki x ima tacno jedan y (niko nije rekao da mora svaki da x da ima razlicit y) i izgleda ovako:
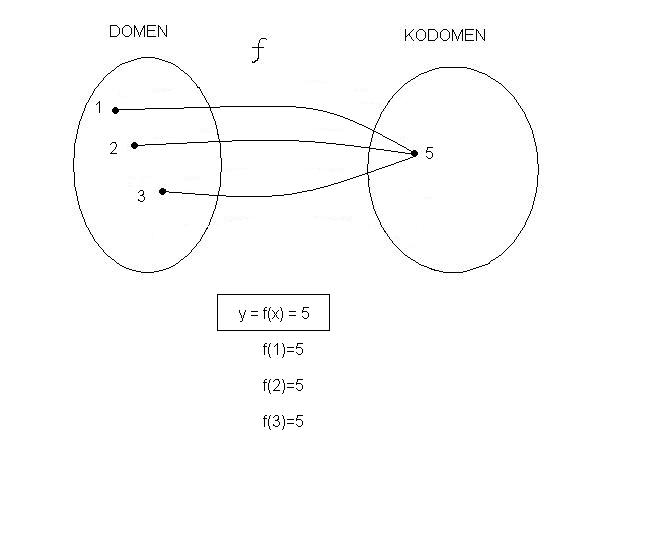 [ demicM @ 16.04.2011. 21:56 ] @
CARE, veliko ti hvala !! Sve mi je sada jasno!
HVALA JOŠ JEDNOM ! Hvala i ostalima! :*
[ markob15 @ 17.04.2011. 03:23 ] @
Ziv bio! Zato smo tu, da pomazemo jedni drugima i sticemo saznanja..
Ajd pa da i ti sledeci put nekog "prosvetlis" ;)
[ miki069 @ 17.04.2011. 09:48 ] @
Provera znanja.
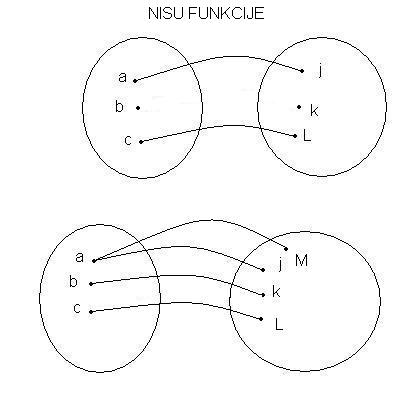
Ako je sve jasno, objasni zašto ova dva preslikavanja nisu funkcije.
 [ demicM @ 17.04.2011. 11:40 ] @
Citat: Provera znanja.
Ako je sve jasno, objasni zašto ova dva preslikavanja nisu funkcije. 
Mislis ova dva preslikavanja?
Kod prve varijante nisu svi elementi domena preslikani. Zapravo, da bi se ostvarila funkcija A u B, za svaki element iz skupa A mora postojati neki element iz skupa B
Kod druge varijante isto ne mozemo da kazemo da je skup A funkcija u B, zato sto svaki element iz domena moze imati samo jednu relaciju sa nekim elementom B.
U ovom slucaju a je vezan i sa m i sa j, odnosno ima dve relacije (dva preslikavanja). [ zzzz @ 17.04.2011. 12:11 ] @
Odličan!Sjedi.
[ miki069 @ 17.04.2011. 12:38 ] @
Odličan.
Sledeće dva preslikavanja jesu funkcije.
Šta druga funkcija ne ispunjava u odnosu na prvu i šta ona nema, a prva funkcija to ima?
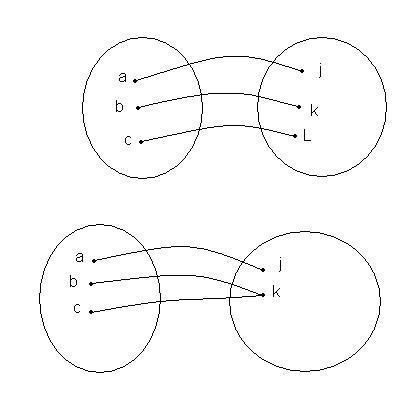 [ demicM @ 17.04.2011. 15:35 ] @
Citat:
Sledeće dva preslikavanja jesu funkcije.
Šta druga funkcija ne ispunjava u odnosu na prvu i šta ona nema, a prva funkcija to ima?
Prva funkcija je bijekcija (svaki element skupa A preslikava se u neki poseban element skupa B, tako da je svaki element skupa B samo u jednoj relaciji sa nekim elementom iz A). Bijekcija je u isto vreme i injekcija i surjekcija.
Druga funkcija je surjekcija. Njoj takoreći fali jedan element u kodomenu, a dva elementa iz domena su u funkciji sa jednim istim elementom kodomena. :) [ miki069 @ 18.04.2011. 01:22 ] @
Vrlodobar.
Sve je tačno, ali nedostaje poenta da prva funkcija ima inverznu funkciju, a druga nema.
Šansa za odličnu ocenu je da navedeš konkretan primer 2 realne funkcije Y=f(X), X je bilo koji realan broj, tako da:
prva bude bijekcija i ima inverznu funkciju, a druga surjekcija i nema inverznu funkciju.
[ demicM @ 18.04.2011. 14:44 ] @
Citat: Sve je tačno, ali nedostaje poenta da prva funkcija ima inverznu funkciju, a druga nema.
Šansa za odličnu ocenu je da navedeš konkretan primer 2 realne funkcije Y=f(X), X je bilo koji realan broj, tako da:
prva bude bijekcija i ima inverznu funkciju, a druga surjekcija i nema inverznu funkciju.
Moze pojasnjenje sta je to inverzna funkcija?? [ edisnp @ 19.04.2011. 00:14 ] @
Ako ti je 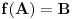 ,bijektivno preslikavanje ,tada sa 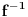 oznacavamo
preslikavanje skupa B u skup A.U tom slucaju 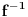 se naziva inverzno preslikavanje
preslikavanja f. [ markob15 @ 19.04.2011. 01:26 ] @
primetices da je domen inverzne funkcije 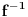 zapravo kodomen polazne funkcije 
(zbog toga je bitno da je funkcija  bijekcija)
[ edisnp @ 19.04.2011. 02:01 ] @
@demicM
da li sad shvatio sta je uospte inverzna funkcija
ako je jesi onda bi se moglo preci na neke prakticne delove
tj.na resavanje nekih zadataka.
[ demicM @ 19.04.2011. 20:46 ] @
edisnp, markob15,
Hvala :)
Citat: miki069
Šansa za odličnu ocenu je da navedeš konkretan primer 2 realne funkcije Y=f(X), X je bilo koji realan broj, tako da:
prva bude bijekcija i ima inverznu funkciju, a druga surjekcija i nema inverznu funkciju.
1. To može biti primer koji je Markob15 dao :)
2. Po mom shvatanju surjekcija ne može nikada biti inverzna, osim ako se radi o bijekciji??
Primer: f: A --> B
---(1 2 3)---
f=
---(a c a)---
Imam još jedno pitanje vezano za jedno objašnjenje iz literature.
Parafraziram: funkcija koja preslikava skup realnih brojeva u sebe definisana je formulom f(x)=2x+4. Ispitati da li se radi o injekciji i bijekciji?
Onda se daje objašnjenje: Iz f(x1) = f(x2), tj. 2x1+4=2x2+4 => x1 = x2, što znači da je funkcija injekcija (1-1). Sa druge strane, ako je y proizvoljan realan broj, onda iz y=2x+4 sledi x = y/2 - 2, što znači da se radi i o bijektivnom preslikavanju.
Meni ovo uopšte nije jasno, jer injekcija znači da se svako različito x preslikava u različito y, odnosno da f(x1) i f(x2) nisu jednaki. A ovde se kaže da su f(x1) i f(x2) jednaki... Može pojašnjenje??
Uzgred, kako su došli do zaključka da je x = y/2 - 2 bijektivno preslikavanje???
Ima još jedna stvar. Ovde se pominju x, x1, x2 i y.
x1 i x2 su elementi, a šta su onda posebno x i posebno y? [ edisnp @ 19.04.2011. 22:36 ] @
Pa vrati se na definicu kad je funkcija injekcija ili 1-1.
[ miki069 @ 19.04.2011. 23:21 ] @
f(x) = 2*x + 4 je bijekcija i ima inverznu funkciju.
f(x) = x^2 nije bijekcija, jer f(2) = f(-2) = 4 i nema inverznu funkciju.
[ demicM @ 29.05.2011. 12:44 ] @
Citat: edisnp: @demicM
da li sad shvatio sta je uospte inverzna funkcija
jesam
----------
Ima tu još par stvari koje mi nisu jasne.
Prva stvar koja mi nije jasna tice se surjekcije i injekcije.
Dakle ja shvatam šta su surjekcija i injekcija sa stanovišta koje ste mi vi objasnili na ovoj temi (graficki) i sa stanovišta reci (kako to objašnjavaju definicije), ali nije mi nije jasno kako je to objasnila literatura (knjiga), pa vas molim da mi objasnite.
Naime u literaturi stoji:

e sad, ja znam da je injektivno preslikavanje takvo preslikavanje da svako razlicito x domena se preslikava u razlicito y kodomena. gornja formula u knjizi kaže da svaki x1 i x2 koje pripada skupu A a pritom je to x1 različito od x2 implicira da f(x1) nije isto kao i f(x2) >>> to je razumljivo, ali problem je u sledećoj "nelogičnosti": ako nam činjenica f(x1) različito od f(x2) govori da se radi o injekciji, zašto se onda spominje da f(x1)=f(x2) implicira da je x1 = x2 ??? ovo je kontradiktorno sa injekcijom
a da stvar bude još zbunjivija za mene, u primeru 2° (podvučeno plavim), upravo to f(x1) JEDNAKO f(x2) se koristi kao način na koji testiramo da li je zadata formula injekcija... ??????? na koji način činjenica x1=x2 i f(x1)=f(x2) govori da se ovde radi o tome da svako različito x u različito y (što se inače naziva injekcija)...
Može pojašnjenje?
----------
Druga stvar koja mi nije jasna tice se jednog zadatka:
Dat je skup A = {a,b,c,d}
f = {(a,b),(b,a),(c,d),(d,c)}
g = {(a,c), (b,a), (c,a), (d,d)}
prvi deo zadatka pita da li su skupovi f i g preslikavanje A u A. JESU i to mi je sasvim jasno
drugi deo zadatka traži da se odrede: f(f(a)), f(f(b)), itd... To mi je jasno, odredio sam.
treci deo zadatka mi nije jasan! tu se traži da rešim jednacinu f(x) = f(g) >>>>>> e taj deo me buni... može pomoc? piše u rešenju da je rešenje b [ demicM @ 29.05.2011. 12:54 ] @
ima još jedna stvar. šta je to g°f (g kružić f)? da li je to preslikavanje funkcije g u funkciju f?
[ edisnp @ 29.05.2011. 13:30 ] @
Evo ti jedan primjer:
Kaze se Naci f kruzic g,ako je 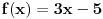 i 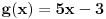 .
Idemo znaci ovako:f kruzic g je isto sto i 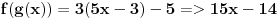 .
I to je to.
Probaj sad da odradis sam neke slicne primjerei bice ti jasno.Kad se f preslikava u g
i kad je obratno. [ demicM @ 30.05.2011. 08:03 ] @
jasno mi je to sad :)
Moze pojasnjenje za 35-ti post?
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|