[ MarijaKg88 @ 17.04.2011. 23:47 ] @
| Mucu me levi i desni limes!Za y=xe^(1/1-x) levi limes u tacki 1(Df je za svako x iz skupa R osim za 1) je + beskonacno a desni je 0.Kako???HITNO |
|
[ MarijaKg88 @ 17.04.2011. 23:47 ] @
[ MarijaKg88 @ 18.04.2011. 00:17 ] @
Ja imam resen zadatak ali ga ne razumem!I nije y=0 vec x=1 asimtota i to samo sa leve strane!!!Horizontalnu i nema jer ima kosu!!!!!!!!Mene samo interesuje kako da resim levi a kako desni limes
[ markob15 @ 18.04.2011. 00:24 ] @
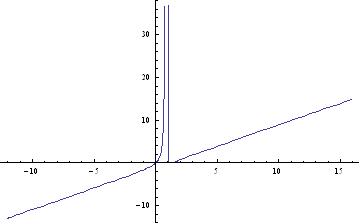
Ovako izgleda tvoja funkcija:
 Kao sto vidis, levi limes u tacki 1 je +beskonacno (odnosno kako se priblizavamo vrednosti x=1 sa leve strane, f(x) se "penje gore"), desni limes u tacki 1 je 0 (jer kada se priblizavamo vrednosti x=1 sa desne strane, f(x) "silazi" do nule). Tako da si tacno izracunala. Takodje, kao sto vidis, ova funkcija ima dve asimptote: vertikalnu (x=1) i kosu. [ SrdjanR271 @ 18.04.2011. 00:29 ] @
U 1+0 limes je 0 i to je ok. Vidi sliku.
 [ markob15 @ 18.04.2011. 00:47 ] @
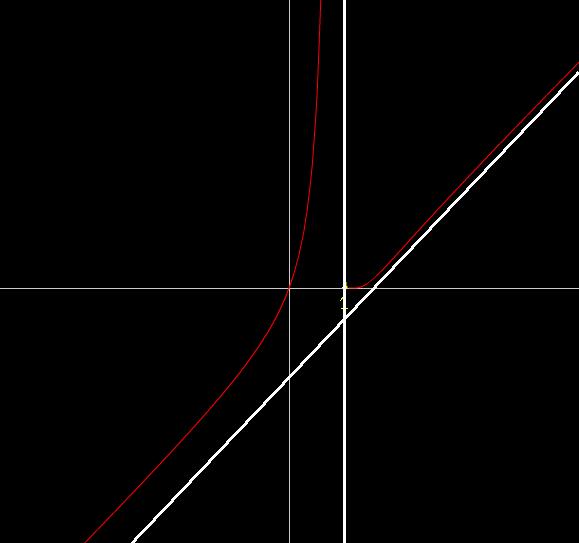
asimptote izgledaju ovako:
 [ miki069 @ 18.04.2011. 01:33 ] @
X=1 je vertikalna asimptota.
Nema veze sa horizontalnom/kosom to šte se za X=1.00...001 dobije da je Y teži ka 0+. Bitno je da se za X=0.999.... dobije Y teži u plus beskonačno. Ne moraju oba limesa biti beskonačno. Dovoljno je jedan da bude beskonačno da bi prekid bio vertikalna asimptota. Oba limesa su određena. Za X=0.999... Y teži ka 1*e^(plus beskonačno) = plus beskonačno. Za X=1.00...001 Y teži ka 1*e^(minus beskonačno) = nula plus. [ MarijaKg88 @ 18.04.2011. 17:09 ] @
Ma ja imam resen zadatak i iscrtan grafik,mene je jedino bunilo kako da izracunam levi tj. desni limes ali sad mi je jasno.
[ miki069 @ 20.04.2011. 00:14 ] @
Šta studiraš i jel u KG-u?
Interesuje me jer je ovo pre Bolonje bio mnogo lak zadatak sa ispita na bilo kom tehničkom fakultetu. Sada je vanredni događaj ako ovakav zadatak padne na ispitu na mašinskom, fizici, hemiji... Moguć je samo na ekonomskom kod Drenovaka ili iz Analize na smeru matematika (informatika) na PMF-u, ako je sa ispita. Komentar je vezan samo za KG. Ne mislim na ETF, FON, građevinu, arhitekturu, saobraćaj... i ostale BG-NS-NIŠ fakultete. Tamo je od matematike nešta i ostalo. Interesuje me kako si odradila n iz kose asimptote Y=k*X + n. To je jedina interesantna stvar u celom zadatku. [ MarijaKg88 @ 20.04.2011. 19:34 ] @
Sto se tice faksa studiram matematiku i informatiku na Pmf u Kg...A sto se tice kose asimtote,nju sam razvila po Tejloru i dobijem je direktno ne radim kao lim f(x)/x za a i lim(f(x)-ax) za b meni je generalno lakse preko Tejlora jer odmah znam kad je grafik iznad a kad ispod kose asimtote.
[ devetkamp @ 22.12.2011. 16:27 ] @
Jel moze neko da mi da funkciju koja ima sve tri asimptote. I horizontalnu i vertikalnu i kosu ?
[ devetkamp @ 22.12.2011. 17:43 ] @
Hvala, pitam, jer nisam bio siguran postoji li funkcija sa svim asimptotama. Cak i ovde na forumu, vidim tvrde, da ako funkcija ima horizontalnu, znaci da nema kosu. Uslov je, valjda, ako funkcija ima horizontalnu asimptotu i u + beskonacno i u - beskonacno, onda sigurno nema kosu. Jel tako?
[ Sini82 @ 22.12.2011. 19:43 ] @
http://matematiranje.com/4_godina.html
Možeš pogledati ovdje i na mnogim drugim mjestima, da ako funkcija ima horizontalnu onda nema kosu asimptotu. Pogledaj formule po kojima se računaju ove dvije asimptote i obrazloži zašto je to tako. [ Sini82 @ 22.12.2011. 20:26 ] @
Lapsus. Tvrđenje koje sam maloprije napisao vrijedi ako funkcija ima horizontalnu asimptotu sa obe strane (i u + i u - beskonačno). Nisam se dovoljno precizno izrazio, ne može sa iste strane da ima i horizontalnu i kosu asimptotu. Navedeni primjer nema horizontalnu asimptotu sa obe strane.
[ devetkamp @ 23.12.2011. 12:50 ] @
E, to je sad u redu. Ako funkcija ima horizontalnu asimptotu samo u + beskonacno, onda moze da ima kosu u - beskonacno. :D
[ devetkamp @ 25.12.2011. 12:01 ] @
I jos nesto: Tvrdjenje da funkcija nema kosu ako ima horizontalnu, vazi za neprekidne funkcije? Jel tako?
[ devetkamp @ 25.12.2011. 12:16 ] @
Nisam ni rekao da jeste. Ova je prekidna, ima sve tri asimptote. Pitanje je bilo, da li to vazi i za neprekidne. tj, da li moze da ima sve tri i neprekidna funkcija?
[ SrdjanR271 @ 25.12.2011. 22:46 ] @
Ako je neprekidna nema vertikalnu.
[ devetkamp @ 28.12.2011. 14:21 ] @
[ darkosos @ 28.12.2011. 14:29 ] @
[ SrdjanR271 @ 28.12.2011. 17:46 ] @
Ima prekid u nuli.
[ Nedeljko @ 28.12.2011. 18:12 ] @
Izvinjavam se, ali moram da intervenišem.
Neprekidnost funkcije se definiše samo na domenu funkcije. U tačkama u kojima funkcija nije definisana ona nije ni neprekidna ni prekidna. Ova funkcija je neprekidna, tj. neprekidna na celom svom domenu, a definisana je samo na pozitivnim realnim brojevima. [ Nedeljko @ 28.12.2011. 18:24 ] @
Citat: SrdjanR271: Ako je neprekidna nema vertikalnu. Pardon, ako je realna funkcija definisana na celom R i neprekidna, onda nema vertikalnu asimptotu. Funkcija 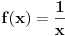 je neprekidna i ima vertikalnu asimptotu je neprekidna i ima vertikalnu asimptotu  . .[ SrdjanR271 @ 28.12.2011. 18:40 ] @
Slažem se, ali 1/x u nuli ima prekid.
[ Sonec @ 28.12.2011. 19:20 ] @
[ SrdjanR271 @ 28.12.2011. 20:39 ] @
Šta onda kažemo za tačku x=0, za f-ju 1/x?
[ Sonec @ 28.12.2011. 20:43 ] @
Citat: Nedeljko:U tačkama u kojima funkcija nije definisana ona nije ni neprekidna ni prekidna. [ SrdjanR271 @ 28.12.2011. 21:00 ] @
Kako onda definišemo prekide? Ili prekidi ne postoje?
Da li se asimptota računa u prekid? Pitam jer mi nije jasno, a ne da bih trolovao. EDIT: Pročitao sam celu temu http://www.elitesecurity.org/t...je-vezi-neprekidnosti-funkcija http://www.elitesecurity.org/p2717644 Citat: Jok, prekid je upravo tačka domena u kojoj funkcija nije neprekidna. On je prve vrste ako postoje oba limesa i konačni su (inače je prekid druge vrste), a otklonjiv ako se vrednost u toj tački može promeniti tako da funkcija bude neprekidna. Vidi definiciju. Može li neki primer takvog prekida? Znači da prekid bude tačka domena, a da nije otklonjiv. [Ovu poruku je menjao SrdjanR271 dana 28.12.2011. u 22:33 GMT+1] [ Sonec @ 28.12.2011. 21:41 ] @
Uzmi na primer funkciju
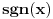 , ona je ocito prekidna funkcija. , ona je ocito prekidna funkcija.Evo, morao sam da uzmem Kadelburga da tacno citiram: Definicija 5.1.2. Za tacku  kazemo da je tacka prekida funkcije kazemo da je tacka prekida funkcije 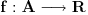 ako ako  nije neprekidna u toj tacki. nije neprekidna u toj tacki.Naglasimo da u skaldu sa ovom definicijom tacka u kojoj neka funkcija nije definisana ne moze biti njena tacka prekida (makar bila i tacka nagomilavanja njene oblasti definisanosti). Tako na primer, tacka  nije tacka prekida funkcije nije tacka prekida funkcije 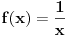 , jer, u skladu sa nasom konvencijom datom u odeljku 4.1, za tu funkciju podrazumevamo da joj je domen , jer, u skladu sa nasom konvencijom datom u odeljku 4.1, za tu funkciju podrazumevamo da joj je domen 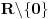 . .Na osnovu stava 5.1.1, tacke prekida realne funkcije  (medju tackama domena koje su ujedno tacke nagomilavanja tog domena) su bilo one tacke (medju tackama domena koje su ujedno tacke nagomilavanja tog domena) su bilo one tacke  kod kojih kod kojih 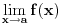 ne postoji, bilo one kod kojih on nije jednak vrednosti ne postoji, bilo one kod kojih on nije jednak vrednosti 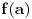 . Uobicajeno je da se tacke prekida klasifikuju na sledeci nacin. . Uobicajeno je da se tacke prekida klasifikuju na sledeci nacin.Definicija 5.1.3. Neka je 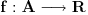 i i  tacka prekida funkcije tacka prekida funkcije  . Kaze se da je u tacki . Kaze se da je u tacki  : :1. prekid prve vrste funkcije  ako postoje konacne granicne vrednosti ako postoje konacne granicne vrednosti 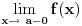 i i 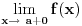 ; ako je ; ako je  tacka nagomilavanja samo jednog od skupova tacka nagomilavanja samo jednog od skupova 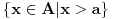 , , 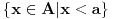 , zahteva se samo postojanje jednog (odgovarajuceg) od tih limesa; specijalno, takav prekid je otklonjiv ako je jos , zahteva se samo postojanje jednog (odgovarajuceg) od tih limesa; specijalno, takav prekid je otklonjiv ako je jos 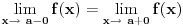 , tj. postoji , tj. postoji 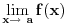 ; ;2. prekid druge vrste funkcije  ako nije prve vrste. ako nije prve vrste.Stav 5.1.1 Neka je 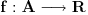 funkcija realne promenljive i funkcija realne promenljive i  tacka nagomilavanja skupa tacka nagomilavanja skupa  . Tada su sledeca tvrdjenja ekvivalentna: . Tada su sledeca tvrdjenja ekvivalentna:1. funkcija  je neprekidna u tacki je neprekidna u tacki  ; ;2. 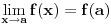 ; ;3. za svaki niz 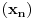 , , 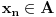 , za koji je , za koji je 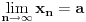 , vazi , vazi 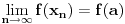 . .Ne mogu sad da pisem ceo odeljak 4.1. Citat: SrdjanR271: Pitam jer mi nije jasno, a ne da bih trolovao. Ti si poznat po tome [Ovu poruku je menjao Sonec dana 28.12.2011. u 23:06 GMT+1] [ Sonec @ 28.12.2011. 21:49 ] @
Citat: SrdjanR271: Može li neki primer takvog prekida? Znači da prekid bude tačka domena, a da nije otklonjiv. Funkcija 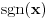 ima u tacki ima u tacki  prekid prve vrste koji je neotklonjiv. Dok funkcija prekid prve vrste koji je neotklonjiv. Dok funkcija 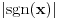 u toj tacki ima otklonjiv prekid. u toj tacki ima otklonjiv prekid.[ miki069 @ 28.12.2011. 22:28 ] @
Ovi decidno kažu da funkcija 1/x u tački x=0 ima prekid druge vrste: http://sh.wikipedia.org/wiki/N...im_vrstama_ta.C4.8Daka_prekida
Ko je sad tu merodavan? Zabuna je u frazi "funkcija je definisana u tački....". [Ovu poruku je menjao miki069 dana 28.12.2011. u 23:43 GMT+1] [ SrdjanR271 @ 28.12.2011. 22:36 ] @
Hvala na trudu Sonec.
Shvatio sam, sta hocete ti i Nedeljko da kažete. Ja i dalje neke stvari ne kapiram, ali nemam više pitanja. [ Sonec @ 28.12.2011. 22:38 ] @
Citat: miki069: Ovi decidno kažu da funkcija 1/x u tački x=0 ima prekid druge vrste: http://sh.wikipedia.org/wiki/N...im_vrstama_ta.C4.8Daka_prekida Ko je sad tu merodavan? Pa u tacki  i jeste prekid druge vrste, nigde nisam (nismo) ni rekli da je prve vrste. i jeste prekid druge vrste, nigde nisam (nismo) ni rekli da je prve vrste.Citat: Nema na cemu [ SrdjanR271 @ 28.12.2011. 22:41 ] @
Citat: Sonec: Pa u tacki i jeste prekid druge vrste, nigde nisam (nismo) ni rekli da je prve vrste. Onda se može reći da je prekidna na R, a neprekidna na R\{0}? [ Sonec @ 28.12.2011. 22:44 ] @
[ miki069 @ 28.12.2011. 22:50 ] @
Nisam ni ja nigde rekao da je prekid prve vrste.
Ako je prekid bilo koje vrste, onda valjda nemamo neprekidnost. Negacija prekidnosti je neprekidnost. Negacija neprekidnosti je prekidnost. Da uprostim pitanje: jel funkcija 1/x prekidna ili neprekidna u x=0? Ili je sva zabuna nastala od one sintagme "ako je funkcija definisana u tački...", a pre toga se ne obrazlaže dobro šta znači da je funkcija definisana u tački...? Imam i ja obe knjige. Kečkić se na kraju poglavlja tako zaplete, da ne verujem da zna i sam šta je hteo da kaže. "Onda se može reći da je prekidna na R, a neprekidna na R\{0}?" Mislim da je ovo jedini ispravan odgovor. [ Sonec @ 28.12.2011. 22:59 ] @
Evo dopuna vezana za poglavlje 4.1:
Pod realnom funkcijom realne promenljive podrazumevacemo svaku funkciju 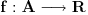 , definisanom na nekom podskupu , definisanom na nekom podskupu  skupa R realnih brojeva i sa vrednostima u R. skupa R realnih brojeva i sa vrednostima u R..... Dogovorimo se odmah o sledecem: ako nije drugacije receno, pod domenom realne funkcije  realne promenljive date analitickim izrazom realne promenljive date analitickim izrazom  podrazumeva se maksimum (u smislu inkluzije) podskupa skupa R koji taj izraz dopusta, tj. podrazumeva se maksimum (u smislu inkluzije) podskupa skupa R koji taj izraz dopusta, tj. 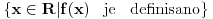 . .Za tacku  sam vec rekao. sam vec rekao.[ Sonec @ 28.12.2011. 23:02 ] @
Citat: Profesor Dragoljub Keckic nije napisao udzbenik iz Analize I. [ SrdjanR271 @ 28.12.2011. 23:05 ] @
Sa http://en.wikipedia.org/wiki/Continuous_function
Citat: Ovo iznad se uklapa u Nedeljkovu, Sonecovu, Kadelburgovu priču. Ali ako ja dobijem zadatak da ispitam i nacrtam ovu f-ju? Ja kod asimptote računam levi i desni limes (petljam oko neprekidnosti), ali ne proveravam da li su jednaki, niti spominjem (nipošto) neprekidnost. Malo mi je ovo mutno. [ miki069 @ 28.12.2011. 23:27 ] @
Od Jovana Kečkića ima knjigu.
Za Dragoljuba sam večeras čuo. Ipak sam ja 1969. godište. Saglasan sam Nedeljkom i Sonecom, ali mu opet deluje šupljo zbog one sintagme. Više me Kečkić uverio u delu kada dokazuje da je Lajbnic poreklom Srbin (lužički), neko kada na kraju poglavlja počne da objašnjava ovo što ste i vi večeras. Možda sam i zaboravio nešta. Idem da čitam Kurepu. Ipak je njegova pretpostavka da je Lajbnic Srbin zbog načina na koji se potpisivao. Kaže da je Nemac ne bi se tako potpisiva. Našta oko onog ich na kraju. Pozdrav. [Ovu poruku je menjao miki069 dana 29.12.2011. u 00:50 GMT+1] [ Nedeljko @ 29.12.2011. 17:06 ] @
SrdjanR271
Slobodno možeš da proveravaš da li su limesi jednaki itd. ali računanje limesa nije isto što i ispitivanje neprekidnosti. To su povezani, ali ne i isti pojmovi. [ darkosos @ 30.12.2011. 08:11 ] @
Citat: Ja kod asimptote računam levi i desni limes (petljam oko neprekidnosti), ali ne proveravam da li su jednaki, niti spominjem (nipošto) neprekidnost. Malo mi je ovo mutno. Jedino sto se u navedenom slucaju moze pitati je da li se funkcija moze dodefinisati tako da bude neprekidna ili slicno, kao npr. 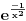 Naravno, ako je takav slucaj, onda neces ni reci da je x=0 asimptota, iako ova tacka prirodno ulazi u pricu o mogucim asimptotama. [ devetkamp @ 01.01.2012. 11:13 ] @
Vi ste se bas potrudili oko ovoga. Svaka vam cast :D
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|