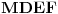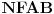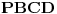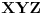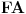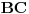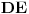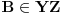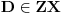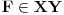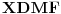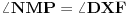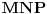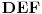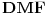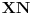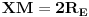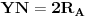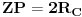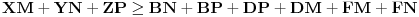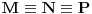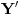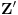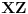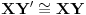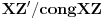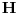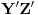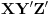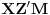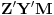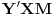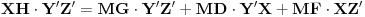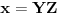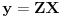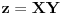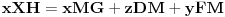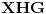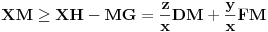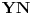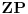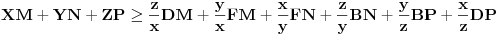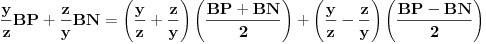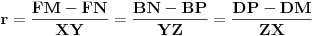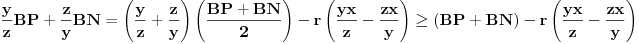Neka pomoć? Recimo - poluprečnik opisane kružnice trougla u funkciji dužina stranica trougla?

Uputstvo za resavanje zadatka:
treba nesto produziti i onda se resava preko sinusne teoreme

Stavio si zvučan naslov, a zadatak je smešno lak, nije mi trebalo više od 20 min. da ga uradim, mada sam možda nešto prevideo jer rešenje stvarno izgleda prosto.

Kao što znamo, za trougao ABC važi da je 2R=a/sinA=b/sinB=c/sinC. U ovom zadatku to koristimo ovako: 2R1=AC/sinB, 2R2=CE/sinD, 2R3=AE/sinF.

Produžimo stranice AF i CD do preseka sa normalama na njih kroz tačke B i E. Tako dobijamo pravougaonik. Očigledno je AC >= stranica koja sadrži tačku B. Dužinu stranice kroz B možemo izraziti na sledeći način: ABsinA+BCsinC. Slično, stranica kroz E je jednaka: DEsinD+EFsinF. Kako su te dve stranice jednake, možemo pisati:
2AC>=ABsinA+BCsinC+DEsinD+EFsinF

Slično, konstruišemo pravougaonike produživanjem preostala dva para stranica, i dobijamo:
2CE>=CDsinC+DEsinE+ABsinB+AFsinF
2AE>=BCsinB+CDsinD+EFsinE+AFsinA

Deljenjem prve jednakosti sa sinB, druge sa sinD i treće sa sinF i sabiranjem dobijamo:
2AC/sinB + 2CE/sinD + 2AE/sinF >= AB(sinA/sinB+sinB/sinD) + BC(sinC/sinB+sinB/sinF) + CD(sinC/sinD+sinD/sinF) + DE(sinD/sinB+sinE/sinD) + EF(sinF/sinB+sinE/sinF) + AF(sinF/sinD+sinA/sinF)

Sada se podsetimo da su naspramne stranice paralelne, što bi značilo jednakost uglova: A=D, B=E, C=F. Posle ovoga postaje očigledno da svaki izraz u zagradi na desnoj strani jednakosti ima oblik k+1/k, a poznato je da je minimalna vrednost svakog izraza ovog oblika jednaka 2, kada je k=1. Znači, sve se svodi na:
4R1 + 4R2 + 4R3 = 2AC/sinB + 2CE/sinD + 2AE/sinF >= onaj dugačak izraz >= 2(AB + BC + CD + DE + EF + AF) = 2P, što je i trebalo dokazati.

Smatram da je ovo korektno rešenje, iako mi i dalje izgleda previše jednostavno za zadatak sa Olimpijade.

U pravu si da je lak kad imas uputstvo,samo sto toga nema na Olimpijadi i niko se nije setio da produzi stranice sem tog jednog lika iz Rumunije koji je 4 godine za redom imao max br. poena na olimpijadama!!!

Evo još jednog rešenja ovog zadatka.

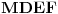
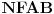
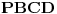
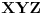
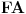
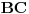
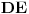
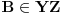
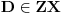
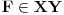
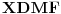
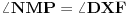
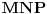
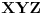
Konstruišimo u datom šestouglu tačke , i takve da su četvoroguli , i paralelogrami. Neka je trougao čije su stranice linije kroz , i normalne na , i , redom, tako da , , . Četvorougao je tetivan pa iz toga sledi da je , i analogno za ostale uglove, pa dobijamo da su trouglovi i slični.

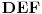
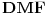
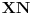
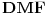
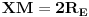
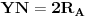
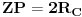
Trouglovi i su podudarni, pa im je poluprečnik opisane kružnice isti. Sa druge strane, je prečnik kružnice opisane oko trougla pa je . Slično, i . Zadatak se sada svodi na dokazivanje sledeće relacije:



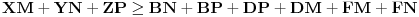
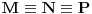
U slučaju ovo zapravo predstavlja Erdeš-Mordelovu nejednakost. U opštem slučaju postupamo na sledeći način.

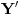
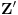
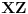
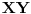
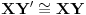
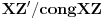
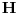
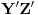
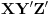
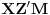
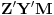
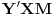
Neka su i tačke na stranicama i , redom, takve da je i . Neka su i podnožja normala iz tačaka , , redom, na . Pošto je površina trougla jednala zbiru površina trouglova , i možemo zapisati ovako:

. \

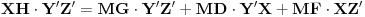
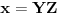
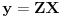
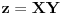
Radi lakšeg zapisa označimo , , . Tada ova relacija postaje:



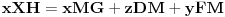
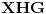
Dalje, pošto je trougao pravougli imamo da je



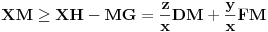
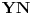
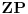
Saberimo ovo sa analognim relacijama za i i dobijamo:



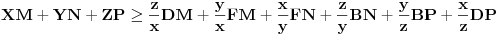
Sad je bitno zapaziti sledeću jednakost:



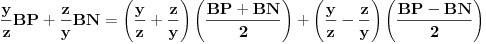
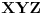
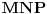
Pošto smo na početku konstatovali da su trouglovi i slični, možemo zapisati:



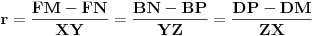
Na osnovu nejednakosti između aritmetičke i geometrijske sredine imamo da je



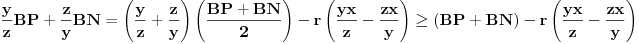
Sabiranjem ovoga sa dve preostale analogne relacije članovi koji sadrže umnožak se međusobno pokrate i ostane nam upravo ono što treba dokazati, čime je zadatak rešen.

a kako to ide na olimpijadi?dobivaš zadatke na engleskom ili na svom jeziku?šta ako netko ne zna engleski??

Dobijas zadatke na svom i engleskom jezika. Resenja pises na kom hoces...

EE ja sam uradio to bez ikakvog sinussa i teorije samo logika i jednacine, ako hoce neko stavicu sliku sa fjesa.

Stavi

mada nisu svi tu koraci neki su ostali na maramici za naocale

_{[Ovu poruku je menjao gygasync dana 23.06.2011. u 20:20 GMT+1]}

Bravo, rešio si slučaj kada je šestougao pravilan. Još samo da rešiš sve ostale slučajeve.

U to se nije ni sumnjalo