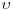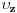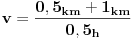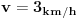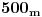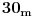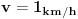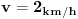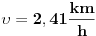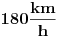[ tszabac @ 21.04.2011. 21:32 ] @
|
| momci malo sam tanak iz izvoda.ko ume neka resi ovaj zadetak.
resenje imam ali nisam do njega dosao racunski.
ide ovako : kolona vojnika dugacka 1 km. krece se brzinom od 1km/h. na kraju kolone se nalazi komandant i on kaze svom zameniku :idi do celnog u koloni i kazi mu...(nebitno za zadatak) i vrati se do mene za tacno sat vremena.
kojom ravnomernom brzinom treba da se krece zamenik da bi se video sa komandantom za tacno jedan sat
pozdrav.... |
[ petarm @ 21.04.2011. 22:17 ] @
Zadatak jeste za decu. Treba znati samo klasicni zakon sabiranja brzina.
Znaci ako definisemo brzinu kolone sa 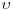 , a brzinu zamenika sa 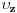 , kojom se relativnom brzinom zamenik u odnosu na kolonu krece u jednom, a kojom u drugom smeru? To ispises i samo treba da nadjes brzinu zamenika 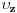 . Vreme je poznato i poznata je duzina kolone koju zamenik prodje 2 puta samo sa drugacijom relativnom brzinom. [ edisnp @ 21.04.2011. 22:18 ] @
Za pola sata kolona ce da predje pola kilometra i sad ako uzmemo da
zamenik treba da krene do cela kolone i da stigne do vrha nje za pola sata
imamo 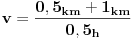 iz ovoga sledi
da nam je za 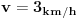 zamenik stigao do vrha kolone i posto treba
da prodje jos pola sata on treba da se vrati nazad za 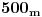 za 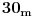
tj.treba da se vrati brzinom 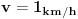 i tad ce da stigne opet na kraj kolone
znaci da on treba da se krece ravnomernom brzinom 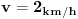 .
Nadam se da je tacno posto zadatak je kao vise za fizicare. [ tszabac @ 22.04.2011. 09:17 ] @
momci zamenik se krece istom brzinom u oba smera.
zadatak jeste komplikovan zbog nepoznanice mesta sastanka sa celnim kolone
pozzzz
[ pctel @ 22.04.2011. 10:22 ] @
Brzine ne treba posmatrati kao apsolutne vec kao relativne (brzina zamenika u odnosu na kolonu). Ta brzina je u jednom smeru v-1 a u drugom v+1. U tom slucaju, relativni predjeni put je u oba smera po 1km.
t=s1/v1+s2/v2=1
1/(v-1) + 1/(v+1)=1 |*(v-1)(v+1)
v+1+v-1=(v-1)(v+1)
2v=v2-1
v2-2v-1=0
v2-2v+1-2=0
v2-2v+1=2
(v-1)2=2
v-1=sqrt(2)
v=sqrt(2)+1
v=2.41 km/s priblizno
Provera:
t1=S/v1=1/(v-1)=1/1.41=0.71h
t2=S/v2=1/(v+1)=1/3.41=0.29h
t1+t2=1h
[ tszabac @ 22.04.2011. 14:32 ] @
cestitam. odgovor je tacan mada mi jos nije jasno tvoje resenje priznajem da je tacno.
pre nekih 5 godina jedan lik (zavrsio fax etf) mi je resio ovaj zadatak preko izvoda.
zaboravio sam postavku resenja ali sam zapamtio rezultat 1+koren iz 2 je brzina zamenika
svaka cast
postavio sam jedan drugi zadatak pogledaj #jedan tezak zadatak#
sa srecom
pozzzz........
[ Shadowed @ 22.04.2011. 14:39 ] @
Citat: tszabac: cestitam. odgovor je tacan mada mi jos nije jasno tvoje resenje priznajem da je tacno.
Koristi kolonu kao referentni sistem. Na taj nacin, zamenik treba da ode 1km i 1km nazad, pri cemu se zna da ce mu brzina u povratku biti za 2km/h veca nego u odlasku. Kada mu izracunas brzine, to su brzine u odnosu na kolonu. Posle je lako samo prebaciti se na okolinu kao koordinatni sistem tako sto dodas/oduzmes brzinu kolone. [ petarm @ 22.04.2011. 17:50 ] @
Citat: pctel: Brzine ne treba posmatrati kao apsolutne vec kao relativne (brzina zamenika u odnosu na kolonu). Ta brzina je u jednom smeru v-1 a u drugom v+1. U tom slucaju, relativni predjeni put je u oba smera po 1km.
t=s1/v1+s2/v2=1
1/(v-1) + 1/(v+1)=1 |*(v-1)(v+1)
v+1+v-1=(v-1)(v+1)
2v=v 2-1
v 2-2v-1=0
v 2-2v+1-2=0
v 2-2v+1=2
(v-1) 2=2
v-1=sqrt(2)
v=sqrt(2)+1
v=2.41 km/s priblizno
Greska se potrala u jedinicama
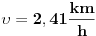 [ petarm @ 22.04.2011. 22:08 ] @
Citat: tszabac: cestitam. odgovor je tacan mada mi jos nije jasno tvoje resenje priznajem da je tacno.
pre nekih 5 godina jedan lik (zavrsio fax etf) mi je resio ovaj zadatak preko izvoda.
zaboravio sam postavku resenja ali sam zapamtio rezultat 1+koren iz 2 je brzina zamenika
svaka cast
postavio sam jedan drugi zadatak pogledaj #jedan tezak zadatak#
sa srecom
pozzzz........
Stvarno ne vidim da ovaj zadatak moze da se resi primenom izvoda. [ miki069 @ 26.04.2011. 14:10 ] @
Možda na ETF-u sve rešavaju preko izvoda.
Nisi obratio pažnju na "lik završio fax ETF".
Zadatak je iz Fizike za Osnovna školu. Maksimalno I godinu srednje škole.
[ petarm @ 26.04.2011. 17:24 ] @
 Pa ok. Moze se od Novog Sada do Zrenjanina doci i preko Zlatibora  Nego ja nemam uopste ideju kako bih ovo resio preko izvoda. Naravno slazem se potpuno da je zadatak za 6. razred Osnovne skole. [ tszabac @ 27.04.2011. 14:23 ] @
momci u opste ne razumem sta je v+1 i v-1 brzina. mozda je pomanjkanje obrazovanja krivo ne nih znao, ali ako zadatak postavis klasicno :
v1=s1/t
v2=(s1+2x)/t
t=1h =cons.
x=put koji ce preci celni dok ga ne stigne zamenik
s1=1km =cons
dobijamo:
t=s1/v1=(s1+2x)/v2
v2*s1=v1*(s1+2x)
v2=v1*(s1+2x)/s1
v2=v1*s1/s1+v1*2x/s1
v2=v1+v1*2x/s1
v2=v1(1+2x/s1)
ovo vec jako lici na resenje. problem je u 2x/s1
zato mislim da je izvod resenje.
pozzzzz.......
[ miki069 @ 27.04.2011. 16:15 ] @
Brzina je vektorska veličina. Ima intenzitet, pravac i smer.
Dve brzine se sabiraju, oduzimaju ili množe kao i svi drugi vektori.
Ne razumem šta nije jasno u rešenju koje je dao PCtel?
V km/h je brzina zamenika u odnosu na referentni sistem (zemlja).
1 km/h je brzina kolone u odnosu na referentni sistem (zemlja).
Pošto su istog pravca: brzina zamenika (V) i brzina kolone (1 km/h) one se sabiraju (oduzimaju) samo zavisno od smera.
(V-1) km/h je brina zamenika u odnosu na kolonu kada ide od komandanta prema čeonom.
(V+1) km/h je brina zamenika u odnosu na kolonu kada ide od čeonog prema komandantu.
Prvi izvod reguliše intervale monotonosti (rašćenja i opadanja) i extremne vrednosti neke zavisne veličine.
To što si ti sa X krstio "put koji ce preci celni dok ga ne stigne zamenik", nema nikakve veze sa izvodima.
Mogao si ga krstiti i sa Y ili Z.
[ petarm @ 28.04.2011. 00:04 ] @
@ tszabac
Zaboravi na kolonu. Vozis auto konstantom brzinom od 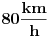 u odnosu na put.To je brzina koja ti je pokazana u automobilu. Pored tebe prolazi u istom smeru automobil konstantnom brzinom 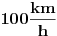 u odnosu na put. On se od tebe udaljava brzinom od 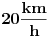 . A da ti je dolazio u susret priblizavao bi ti se brzinom 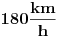 . Da li je sada jasno? [ tszabac @ 29.04.2011. 13:59 ] @
jeste. na taj nacin nisam imao prilike da radim zadatke. ipak sam samo studirao visu etf i imao poklonjeno 6 iz matematike.
jasan je sistem rada. svaka cast. zadovoljstvo je cuti i videti majstore na delu...
samo napred. ako neki zadatak zanimljiv iscackam stavicu na mrezu
pozzz.....
[ tszabac @ 26.01.2012. 22:05 ] @
crv u glavi mi nije dao mira pa sam posle nekog vremena seo i resio zadatak klasicno analiticki.
ako posmatramo brzine jednog i drugog do momenta kada zamenik dodje do celnog imamo:
V1=brzina kolone
V2=brzina zamenika
s=1km
x=tacka susreta zamenika i celnog
V1=x/t
v2=(s+x)/t
kada izjednacimo preko t dobijemo: x/V1=(s+x)/v2 V2=V1(s+x)/x V2=V1(1+s/x)
ako sada gledamo brzinu od momenta kada je zamenik stigao celnog pa do susreta sa komandantom imamo:
V1=(s-x)/t
V2=x/t
kada izjednacimo preko t imamo (s-x)/V1=x/V2 V2=V1x/(s-x) V2=V1(x/(s-x))
iz uslova zadatka brzina u oba pravca je ista pa imamo
V1(1+s/x)=V1(x/(s-x)) 1+s/x=x/(s-x) (x+s)/x=x/(s-x) (s+x)/x=x/(s-x) s*2-x*2=x*2 s*2=2x*2
x=s/sqrt(2)
ako sada uvrstimo x u jednu od jednacina imamo: V2=V1(1+s/x) V2=V1(1+sqrt(2)s/s) V2=V1(1+sqrt(2))
sto je krajnje resenje.
pozzz....
[ kandorus @ 27.01.2012. 03:48 ] @
Za vreme t[h] (< 1) zamenik će stići prvog vojnika na čelu kolone. Za isto vreme t vojnik na čelu kolone će preći t[km] puta pa je ukupan put koji zamenik ima da predje dok ne stigne prvog vojnika (1+t)[km]. Zato je brzina kretanja zamenika
v = (1+t)/t
Zamenik mora da se vrati t[km] i to za vreme (1-t)[h] pa je
t = v(1-t)
Odnosno
t/(1-t) = (1+t)/t
t² = 1 - t²
t = 1/√2
v = (1 + 1/√2) / (1/√2) = 1 + √2
Da, stvarno zadatak za osnovnu.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|