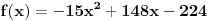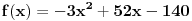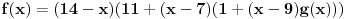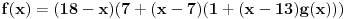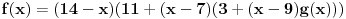[ nikolinv @ 22.04.2011. 20:15 ] @
|
| Petar: "Gde si dobio taj ružan polinom f(x) sa tako mnogo nepoznatih koeficijenata? Izgleda užasno".
Pavle: "To je polinom sa celobrojnim koeficijentima i jedan od njegovih korena je tačno broj godina moje ćerke Marije".
Petar: "Bilo kako bilo izgleda mučno. Daj da izračunam f(7). Nažalost, dobio sam 77, a ne nulu".
Pavle: "Ti ne znaš koliko je Marija stara, ali ona ima više od 7 godina".
Petar: "Tada daj da pokušam sa godinama mog sina Jovana. Gle, dobih 85!"
Pavle: "Pazi Petre, Marija je starija nego tvoj sin".
Koliko godina ima Jovan, a koliko Marija?
|
[ SrdjanR271 @ 23.04.2011. 13:51 ] @
Evo jedno rešenje.
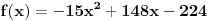
I u ovom slucaju Jovan ima 3 , a Marija 8
[ nikolinv @ 23.04.2011. 15:18 ] @
Izvinjenje Srđanu, ali i Jovan ima više od 7 godina, tj. poslednja rečenica glasi:
Pavle: "Pazi Petre, Marija je starija nego tvoj sin, mada i on ima više od 7 godina".
Rešenje je jedinstveno, ali polinom nije.
[ SrdjanR271 @ 23.04.2011. 16:38 ] @
No problemo.
Onda je
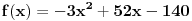
Marija ima 14, a Jovan 9 godina.
[ Nedeljko @ 23.04.2011. 17:16 ] @
Koliko vidim, ima dva rešenja.
1. Marija ima 14, Jovan 9 godina, a polinom je oblika
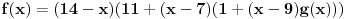
,
2. Marija ima 18, Jovan 13 godina, a polinom je oblika
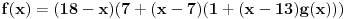
.
U oba slučaja je
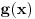
proizvoljan polinom sa celim koeficijentima.
[ SrdjanR271 @ 23.04.2011. 17:38 ] @
@Nedeljko
Mislim da će tvoj polinom "davati" 65 umesto 85. A za ostalo daje dobar rezultat (77 i 0).
Ovako je ok za prvi umesto jedan treba da bude 3.
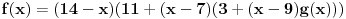
A drugi mislim da ne može, tj. da je jedinstveno rešenje 14 i 9.
A kao što si ti napisao g(x) je proizvoljan.
Za g(x)=0 dobija se polinom koji sam ja napisao
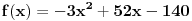 [Ovu poruku je menjao SrdjanR271 dana 23.04.2011. u 18:59 GMT+1]
[Ovu poruku je menjao SrdjanR271 dana 23.04.2011. u 19:00 GMT+1]
[Ovu poruku je menjao SrdjanR271 dana 23.04.2011. u 18:59 GMT+1]
[Ovu poruku je menjao SrdjanR271 dana 23.04.2011. u 19:00 GMT+1][ Nedeljko @ 23.04.2011. 19:57 ] @
Da, da, moja greška je bila što sam računao da je 85/5=17. Eto, šta da se radi.
[ nikolinv @ 23.04.2011. 23:22 ] @
Konačno sam našao elementarno rešenje ovog zadatka:
m - Miličine godine
j - Jovanove godine
f - polinom
u,v - pomoćni polinomi
Važi:
f(m) = 0
f(7) = 77
f(j) = 85
m > j > 7
0. Neka je f neki polinom i neka f(a) = b , (a i b brojevi) tada se polinom f može zapisati:
f(x) = (a - x)*g(x) + b
gde je g takođe polinom. Specijalno, ako je k koren polinoma (f(k) = 0), onda:
f(x) = (k - x)*g(x)
1. Kako je m koren polinoma f imamo:
f(x) = (m-x)*u(x)
gde je u polinom sa celobrojnim koeficijentima.
Za x = 7,
f(7) = (m - 7)*u(7)
77 = (m - 7)*u(7)
(m-7) | 77 (*)
Za x = j,
f(j) = (m - j)*u(j)
85 = (m - j)*u(j)
(m - j) | 85 (**)
2. Kako je f(7) = 77, to na osnovu 0. možemo funkciju f zapisati i ovako:
f(x) = (x - 7)*v(x) + 77
Za x = j,
f(j) = (j - 7)*v(j) +77
85 = (j - 7)*v(j) + 77
8 = (j - 7)*v(j)
(j - 7) | 8 (***)
Na osnovu (*) zaključujemo da je m element skupa {14,18,84}
Na osnovu (***) zaključujemo da je j element skupa {8,9,11,15}
Kako i uslov (**) mora biti zadovoljen, formiramo sve razlike kandidata za m i za j. Dobija se skup 3,5,6,7,9,10,69,73,74,76 gde je jedino broj 5 deli broj 85. Kako smo 5 dobili kao razliku brojeva 14 i 9, to je
m = 14 , j = 9
što je očigledno i jedino rešenje zadatka.
Polinom je moguće sada tražiti u obliku kvadratnog trinoma (partikularno rešenje), jer znamo tri njegove vrednosti, ali se to u zadatku i ne traži.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.