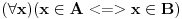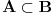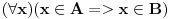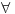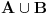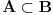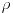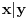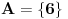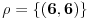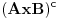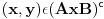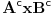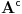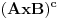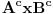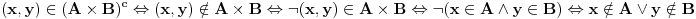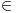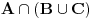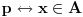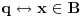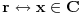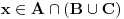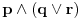|
|
[ Hari Haler @ 24.04.2011. 10:25 ] @
|
| pozdrav svima,
imam par pitanja pa bih zamolio sve upućene da odgovore kad nađu vremena.
na koji način "čitamo" (tumačimo) ovakav zapis:
A=B ako i samo ako (∀x)(x∈A ⇔ x∈B)
A⊂B ako i samo ako (∀x)(x∈A ⇒ x∈B)
interesuje me i ovo.
teorema: za skupove A i B važi: A=B ako i samo ako A⊂B i B⊂A.
kao dokaz, navodi se da je dovoljno to što je iskazna formula
(p⇔q)⇔(p⇒q)⋀(q⇒)
tautologija.
pretpostavljam da smo do formule došli jednostavno zamjenjujući x∈A sa p i x∈B sa q u gornjim formulama i zbog znaka jednakosti u teoremi stavili logički veznik ⇔?
svako dobro
[Ovu poruku je menjao Hari Haler dana 25.04.2011. u 20:33 GMT+1] |
[ edisnp @ 24.04.2011. 11:37 ] @
A=B ako i samo ako 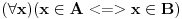
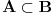 ako i samo ako 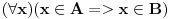
da bi mogao ovako nesto da procitas morao bi da znas sta znace kvantifikatori univerzalni
i egzistencijalni 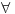 - univerzalni kvantifikator a  -znaci za svako x. [ Hari Haler @ 24.04.2011. 12:04 ] @
znam šta znače univerzalni kvantifikatori, a i logički veznici ili operacije ekvivalencije i implikacije, ali zanima me kako "čitamo" drugi dio u zagradi.
[ Hari Haler @ 24.04.2011. 12:12 ] @
ustvari, kad bolje razmislim, pretpostavljam da bi se to moglo protumačito kao: A=B ako i samo ako, je za svaki x tačna logička formula ekvivalencije iz zagrade, odnosno kada su oba izraza sa lijeve i desne strane znaka ekvivalencije ili tačni ili netačni. u drugom slučaju pretpostavljam da se može rezonovati slično: implikacija neće biti tačna samo ako x∈A, ali x∉B.
[ edisnp @ 24.04.2011. 12:17 ] @
A=B ako i samo ako 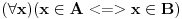
ovo citamo kao:skup A je jednak kskupu B ako i samo ako je za svako x koje je elemenat skupa A sledi da je i x elemenat skupa B i obratno.
a drugi iskaz znaci:Skup A je podskup skupa B ako i samo ako vazi za svako x koje je elemanat skupa A sledi da je i x elemenat skupa B , naravno u ovoj situaciji ne vazi i obrnuta relacija jer je u pitanju implikacija a kod prve vazi jer je u pitanju ekvivalencija.Nadam se da je jasno.  [ Hari Haler @ 24.04.2011. 13:35 ] @
crystal clear 
slobodno nastavi dalje sa odgovorima  [ edisnp @ 24.04.2011. 13:54 ] @
I'm os glad.
kakvim odgovorima.
[ Nedeljko @ 24.04.2011. 18:59 ] @
Odatle sledi da je {1,2}={1,1,2,2}. Skup ne zna za ponavljanja, nego samo da li nekog objekta ima ili nema.
[ edisnp @ 24.04.2011. 19:41 ] @
To bi bio isto kao kad bi se trazila na primer unija dva skupa A i B
A={1,1} i B={2,2}, 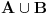 ={1,2} a ne bi bilo 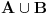 ={1,1,2,2}. [ Nedeljko @ 24.04.2011. 22:06 ] @
Obzirom da je A={1,1}={1} i B={2,2}={2}, njihova unija je {1,2}={1,1,1,1,2,2,2} itd.
Dakle, unija im se može napisati na oba načina - kao {1,2} i kao {1,1,2,2}.
[ edisnp @ 24.04.2011. 22:59 ] @
Znaci li na primer ako pravimo razliku skupa A i skupa B tj.
da li se pise samo A razlika B={1,1} ili samo {1} ili {1,1,1,1,1 itd}.
[ Nedeljko @ 25.04.2011. 12:05 ] @
Obično se svaki element navodi po jedanput, ali nije nikakva greška navesti ga više puta.
[ Hari Haler @ 25.04.2011. 19:42 ] @
nije mi jasno zašto je relacija jednakosti relacija parcijalnog uređenja? očigledno je refleksivna, simetrična i tranzitivna, ali nije mi jasno zašto je i antisimetrična?
uzgred, edisnp, mislio sam da nastaviš sa odgovorima koje sam postavio na početku temu. ako ih znaš. nedeljko i tvoji odgovori su dobrodošli. obrisao sam primjer iz prvog posta pošto sam napravio grešku u kucanju, a ovo za elemente skupa ("skup ne zna za ponavljanje") i proizilazi iz definicije jednakosti dva skupa. dobro je da si ukazao na to.
[ edisnp @ 25.04.2011. 20:48 ] @
Relacija  je refleksivna ,antisimetricna i tranzitivna i naziva se relacija parcijanog uredjenja .
Ako su u relacija parcijalnog uredjenja  bilo koja dva elementa uporediva onda kazemo da je skup tom relacijom potpuno uredjen dok relaciju  nazivamo relacijom totalnog uredjenja.
A za pitanje da dokazes da za skupove A i B vazi A=B ako i samo ako je 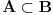 i  predlazem ti da dokaz izvedes najednostavnije moguce a to je pomocu Ojler-Venovih dijagrama.I jos za relacije koje se odlikuju osbina:refleksivnost antisimetricnost i tranzitivnost nazivaju se relacijama poretka. [ Nedeljko @ 25.04.2011. 22:23 ] @
Zašto je jedankost antisimetrična? Pa, probaj da to utvrdiš po definiciji antisimetričnosti. Da li iz a=b i b=a sledi a=b?
[ edisnp @ 25.04.2011. 22:53 ] @
Evo napisao sam ti jedan zadatak:
Dat je skup  ={6,6}, i u njemu je definisana relacija 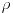 sa 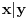 Ispitati osbinu relacije 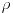 . [ Nedeljko @ 26.04.2011. 09:30 ] @
Dakle, 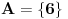 , 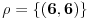 . Ova relacija je zapravo jednakost na jednočlanom skupu. Ima osobine refleksivnosti tranzitivnosti simetričnosti i antisimetričnosti. [ Hari Haler @ 26.04.2011. 10:52 ] @
Citat: Nedeljko: Zašto je jedankost antisimetrična? Pa, probaj da to utvrdiš po definiciji antisimetričnosti. Da li iz a=b i b=a sledi a=b?
slijedi. ali nekako mi je, ne znam..to slijedi odmah iz prvog a=b :)
Citat: Nedeljko: Dakle, 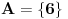 , 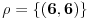 . Ova relacija je zapravo jednakost na jednočlanom skupu. Ima osobine refleksivnosti tranzitivnosti simetričnosti i antisimetričnosti.
tranzitivnosti?
uzgred, kako pišete formule da vam izgledaju tako?
[ Hari Haler @ 26.04.2011. 11:50 ] @
našao sam da je po definiciji uređeni par (a,b)={{a},{a,b}}. u tom slučaju, mislim da mi je jasno zašto je relacija rho={(6,6)} tranzitivna. da li se uređeni par i definiše na taj način da bi između elemenata jednog uređenog para postojala relacija poretka?
[ edisnp @ 26.04.2011. 11:58 ] @
Iz definicije antisimetricnosti ili koja je definisana na sledeci nacin dakle svako x i y koji
su elemnti nekog skupa A gde je x u relaciji sa y i y u relaciji sa x naravno iz ovoga sledi da je x=y
na onom primeru sto sam ti napiso imas da je relacija ro definisana sa x|y tj. da se x sadrzi u y i
ro={(6,6)} posto je uzmi sad da ti je prvi broj u relaciji tj. 6=x a y drugi tj.isto y=6 iz ovoga sledi da se
x sadrzi u y a posto je x=y sledi i da se y sadrzi u x i time je uslov antisimetricnosti ispunjen naravno relacija
ima i sve ostale osobine ali sam je napisao jer si na njoj odma mogo da uvidis antisimetricnos.A sto se tice pitanja
oko formula moras koristi Latex sve vezano za to mozes naci ovdje http://www.elitesecurity.org/t35291-Sve-La-TeX-na-ovom-forumu. [ Nedeljko @ 26.04.2011. 13:28 ] @
Citat: Hari Haler: slijedi. ali nekako mi je, ne znam..to slijedi odmah iz prvog a=b :)
Pa? U čemu je problem?
Citat: Hari Haler: našao sam da je po definiciji uređeni par (a,b)={{a},{a,b}}. u tom slučaju, mislim da mi je jasno zašto je relacija rho={(6,6)} tranzitivna. da li se uređeni par i definiše na taj način da bi između elemenata jednog uređenog para postojala relacija poretka?
To je jedan od mogućih definicija uređenog para. Ujedno je i najpopularnija, jer je najjednostavnija. Međutim, suština uređenog para je us ledećem:
1. Od ma kakvih objekata a i b mogu da formiram objekat koji označavam sa (a,b).
2. Objekti (a,b) i (c,d) su jednaki akko je a=b i c=d. [ Hari Haler @ 28.04.2011. 15:29 ] @
valjda ni u čemu :)
ako biste još bili ljubazni da odgovorite i na drugi dio prve poruke.
svako dobro
p.s edisnp, hvala za link.
[ Sini82 @ 28.04.2011. 16:57 ] @
edisnp ti je odgovorio.
[ Hari Haler @ 28.04.2011. 23:34 ] @
Citat: Sini82: edisnp ti je odgovorio.
edisnp je odgovorio da dokaz izvedem pomoću ojler-venovih dijagrama. a moje pitanje je išlo ovako:
za skupove A i B važi: A=B ako i samo ako A⊂B i B⊂A.
kao dokaz, navodi se da je dovoljno to što je iskazna formula
(p⇔q)⇔(p⇒q)⋀(q⇒p)
tautologija.
pretpostavljam da smo do formule došli jednostavno zamjenjujući x∈A sa p i x∈B sa q u gornjim formulama i zbog znaka jednakosti u teoremi stavili logički veznik ⇔?
[ Nedeljko @ 29.04.2011. 08:59 ] @
Da.
[ Hari Haler @ 29.04.2011. 10:31 ] @
zahvaljujem 
i moram priznati momci da ste prilično teški za saradnju 
čujemo se ponovo.
svako dobro
[Ovu poruku je menjao Hari Haler dana 29.04.2011. u 20:03 GMT+1][ cikin @ 22.10.2012. 16:44 ] @
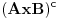 e sad iz ovog sledi 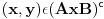 ( e sad ne znam ove sve imbole pa zato cu ovako) sad znam da x ne pripada A, tj. da pripadaju  tako i za y... e sad mi je probem da dokazem da za pocetnu formulu vazi 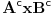 ... probem mi je kako da zapisem ovo x...npr , x pripada 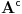 (ovde znam sta) y pripada  [Ovu poruku je menjao cikin dana 22.10.2012. u 19:11 GMT+1]
[Ovu poruku je menjao cikin dana 22.10.2012. u 19:11 GMT+1][ darkosos @ 23.10.2012. 10:09 ] @
Napisao si sve to malo zbrda-zdola i ne vidi se jasno sta u stvari dokazujes? Pocinjes bez ikakvog uvoda izrazom 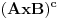 a odatle nista ne sledi...
Posto pominjes 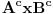 i odnos ovog izraza sa onim sa pocetka, prepostavicu da pokusavas da dokazes da je to isto... Ali to nije isto. Mozda ti pomogne ovakvo rezonovanje:
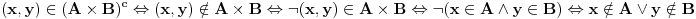 [ cikin @ 03.11.2012. 11:10 ] @
samo da pitam ove skupovne indentite kako da dokazujem... da ove preseke, unije zamenjujem sa konjunkcijom, dosjunkcijom itd.... ili ovako... jer kako sam cuo ne smem da koristim oznako za 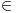 jer ne postoji u logici....al opet ne znam kako bih napisao AxB
[Ovu poruku je menjao cikin dana 03.11.2012. u 12:31 GMT+1][ darkosos @ 04.11.2012. 14:21 ] @
Za ovu metodu moras koristiti znak pripadnosti skupu, ali na sledeci nacin:
Npr. skupovni izraz 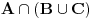 prebacujes u logicki tako sto stavis da je 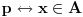 , 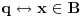 i 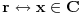 .
Tako se 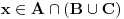 prebacuje u 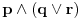 .
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|