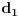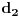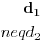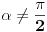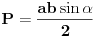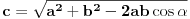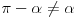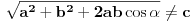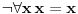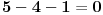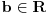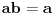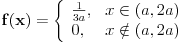|
|
[ nikolinv @ 30.04.2011. 20:20 ] @
|
| Neka su a i b stranice paralelograma ABCD, a d1 i d2 njegove dijagonale. Trouglovi ABC (sa stranicama a, b i d1) i ABD (sa stranicama a, b i d2) su jednake površine, ista stranica a i ista visina h.

Neka je H(p,q,r) Heronov obrazac za trougao čije su stranice p,q i r. Tada važi:
H(a,b,d1) = H(a,b,d2)
iz čega zaključujemo da važi:
d1=d2
tj. svaki paralelogram je ustvari pravougaonik!!!
|
[ igorpet @ 30.04.2011. 20:51 ] @
Ako dva trogla imaju dve strane iste i visinu (tj. imaju iste povrsine) ne znaci da ce im i treca strana biti jednaka, jer to zavisi od ugla koje one zaklapaju a u ovom slucaju su to razliciti uglovi.
Tako da d1 nije jednako d2.
Ili mozda ja negde gresim?
[ edisnp @ 30.04.2011. 21:53 ] @
Naravno da gresis.Kad su dijagonale kod paralelograma jednake nikad
ako su jednake onda je to pravougaonik ili kvadrat.U situaciji
koju je postavio nikolinv nisu dijagonale jednake jer posmatrajmo trouglove
ABC i ABD da bi dokazo da su dijagonale jednake moras dokazati da su
trouglovi ABC iABD podudarni znaci imamo da su ime jednake po dve stranice jednake
i sad nam fali treci element kojeg nikad necemo naci jer ga nema jer nijedan od uglova datog trougla
unutrasnjih nije isti.
[ pexi92 @ 30.04.2011. 22:49 ] @
H nije 1-1
tu gresis
[ edisnp @ 30.04.2011. 23:00 ] @
Kako to mislis nije 1-1 ako mislis za visinu trouglova ABC i ABD onda onda su im visine jednake .
[ pexi92 @ 30.04.2011. 23:26 ] @
ne ti nikolinv gresi
funkcija H nije 1-1 pa iz H(a,b,d1)=H(a,b,d2) ne sledi d1=d2
[ vincent33 @ 30.04.2011. 23:30 ] @
Neka je F funkcija = x^2+2x.
F(-2)=F(0)
Da li to znači da je -2 jednako 0? Ne.
Citat: Kako to mislis nije 1-1 ako mislis za visinu trouglova ABC i ABD onda onda su im visine jednake . [ nikolinv @ 30.04.2011. 23:36 ] @
Ali funkcija H je 1-1, zašto ne bi bila?
[ pexi92 @ 30.04.2011. 23:46 ] @
To bi onda znacilo da dva trougla sa istim povrsinama imaju iste strane
H nije 1-1 to se moze i analiticki proveriti vrlo lako
[ Nedeljko @ 01.05.2011. 01:25 ] @
Evo kako izgleda funkcija h(1,1,x) na intervalu (0,2). Očigledno nije 1-1.
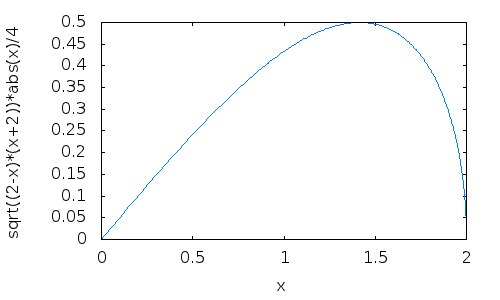 [ dusan2309 @ 01.05.2011. 09:34 ] @
Evo lakseg nacina za objasnjenje zasto je pravougaonik vrsta paralelograma.
Definicija paralelograma glasi: Paralelogram je cetvorougao cije su naspramne stranice paralelne.
Paralelogram ciji su svi uglovi pravi naziva se pravougli paralelogram (tj. pravougaonik)
Znaci, pravougaonik je vrsta paralelograma.
Kvadrat je specijalni pravougaonik, tj. kvadrat je pravougaonik koji ima sve stranice jednake.
Znaci, pravougaonik je vrsta paralelograma, a kvadrat je vrsta pravougaonika.
[ edisnp @ 01.05.2011. 12:09 ] @
Romb je isto vrsta paralelograma cije su sve strane jednake
prosto receno romg je kosougli kvadrat.:)
[ nikolinv @ 01.05.2011. 12:40 ] @
Heronov obrazac možemo zapisati kao:
P2 = s(s-a)(s-b)(s-c), s=(a+b+c)/2
16P2=(a+b+c)(-a+b+c)(a-b+c)(a+b-c)
Potrebno je malo algebre da se pokaže da vredi:
16P2=2[(ab)2+(bc)2+(ca)2]-(a4+b4+c4)
Iz H(a,b,d1)=H(a,b,d2) imamo:
2[(ab)2+(bd1)2+(d1a)2]-(a4+b4+d14)=2[(ab)2+(bd2)2+(d2a)2]-(a4+b4+d24)
2d12(a2+b2)-d14=2d22(a2+b2)-d24
2(a2+b2)(d12-d22)=(d14-d24)
i konačno:
2(a2+b2)(d12-d22)=(d12+d22)(d12-d22)
Iz poslednjeg izraza sledi da dijagonale d1 i d2 nisu nužno jednake.
Kuriozitet je da ako s razlogom predpostavimo da d1<>d2 i poslednji izraz podelimo sa (d12-d22), dobijamo tzv. Parallelogram Law:
2(a2+b2)=(d12+d22)
[ Nedeljko @ 01.05.2011. 13:39 ] @
Izvođenje ti nije kompletno, jer nisi dokazao da postoje  i  takvi da postoje 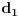 i 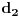 tako da je 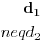 i da je takav paralelogram moguć.
Neka su  i  dužine ivica trougla koje zaklapaju ugao 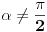 . Površina tog trougla je 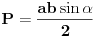 a preostala stranica 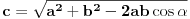 . Ako uočimo trougao sa dvema stranicama dužina  i  koje zaklapaju ugao 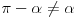 , onda je površina odgovarajućeg trougla ista, a preostala stranica je 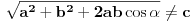 . [ nikolinv @ 01.05.2011. 15:15 ] @
Nedeljko, uz svo poštovanje, mislim da se otišlo predaleko. Naime, do sada smo utvrdili aklamacijom da je u "Paradoksu" implicitno podrazumevano da je funkcija H (Heronov obrazac) ustvari 1-1. Onda si ti grafikom pokazao da funkcija H(1,1,x) nije 1-1. Moje poslednje izvođenje dokazuje to isto, samo opštije, tj. za funkciju H(a,b,x), tako da je ovo čisto algebarski problem, pa ne treba dokazivati egzistenciju nikakvog paralelograma, jer smo geometriju isključili iz rasprave, zar ne?
[ poligonX @ 01.05.2011. 17:38 ] @
Neki su vec pominjali paradoks u matematici...i bili su banovani. Nedeljko je lepo objasnio na toj temi, da paradoks u matematici ne postoji. Bilo bi glupo da se opet vracamo na to. Cisto da znas sta bi moglo da te snadje.
[ Nedeljko @ 01.05.2011. 17:54 ] @
Po Bojanovom obrazloženju, nisu banovani zbog onoga o čemu su pričali, već zbog toga kako su pričali. [ igorpet @ 01.05.2011. 18:21 ] @
Citat: poligonX: Neki su vec pominjali paradoks u matematici...i bili su banovani. Nedeljko je lepo objasnio na toj temi, da paradoks u matematici ne postoji. Bilo bi glupo da se opet vracamo na to. Cisto da znas sta bi moglo da te snadje.
Ovu tvoju tvrdnju bih uzeo sa rezervom.
Mi ovde govorimo o Euklidskoj geometriji i relativno malim geometrijskim figurama.
Npr. paradoks moze biti da zbir uglova u trouglu nije uvek 180 stepeni ili da Pitagorina teorema ne vazi bas za sve trouglove i u svim slucajevima.
Ali ovi paradoksi (ili mozda je bolje reci specijalni slucajevi) su vec prouceni i dokazani, pa zato i nisu paradoksi, ali ako su neki postojali sa kojom verovatnocom mozemo tvrditi da vise ne postoji ni jedan paradoks?
Revolucija koja je u matematici napravljena, i u fizici, koja je nastala otkrićem teorije relativnosti i kvantne mehanike a kojoj je prethodilo otkrice ne-Euklidskih geometrija je dovela do nekih paradoska u matematici koji do tada nisu bili poznati. [ poligonX @ 01.05.2011. 18:36 ] @
Citat: igorpet: Ovu tvoju tvrdnju bih uzeo sa rezervom.
Mi ovde govorimo o Euklidskoj geometriji i relativno malim geometrijskim figurama.
Npr. paradoks moze biti da zbir uglova u trouglu nije uvek 180 stepeni ili da Pitagorina teorema ne vazi bas za sve trouglove i u svim slucajevima.
Ali ovi paradoksi (ili mozda je bolje reci specijalni slucajevi) su vec prouceni i dokazani, pa zato i nisu paradoksi, ali ako su neki postojali sa kojom verovatnocom mozemo tvrditi da vise ne postoji ni jedan paradoks?
Revolucija koja je u matematici napravljena, i u fizici, koja je nastala otkrićem teorije relativnosti i kvantne mehanike a kojoj je prethodilo otkrice ne-Euklidskih geometrija je dovela do nekih paradoska u matematici koji do tada nisu bili poznati.
Pa dobro i ja sam malo bio zbunjen zato sto je Nedeljko utvrdio da su matematicka i filozofska logika isto, a onda, da paradoks u matematici ne postoji. A filozofska logika priznaje postojanje paradoksa. (Inace ta rec ne bi ni postojala?). Samo sam hteo da upozorim korisnika nikolinv da su neki bili banovani zato sto su tvrdili da postoji paradoks u matematici, kako god, i na koji nacin oni to rekli, jer mozda nije procitao tu temu. [ igorpet @ 01.05.2011. 18:40 ] @
Citat: poligonX: Pa dobro i ja sam malo bio zbunjen zato sto je Nedeljko utvrdio da su matematicka i filozofska logika isto, a onda, da paradoks u matematici ne postoji. A filozofska logika priznaje postojanje paradoksa. (Inace ta rec ne bi ni postojala?). Samo sam hteo da upozorim korisnika nikolinv da su neki bili banovani zato sto su tvrdili da postoji paradoks u matematici, kako god, i na koji nacin oni to rekli, jer mozda nije procitao tu temu.
Ne, banovani su jer nisu znali da navedu primer a tvrdili su da paradoksi postoje
Ja sam naveo cak 2 primera, pa se nadam da nisam kandidat za banovanje  [ poligonX @ 01.05.2011. 18:46 ] @
Hm...vidim da nisi procitao celu temu. Boxxter je naveo Curryev paradoks.
http://www.elitesecurity.org/t...-matematicke-filozofske-logike[ igorpet @ 01.05.2011. 18:50 ] @
Primer nije bio ubedljiv i osporen je kao paradoks 
Ja sam dao jacu argumentaciju  [ Nedeljko @ 01.05.2011. 19:13 ] @
Citat: igorpet: sa kojom verovatnocom mozemo tvrditi da vise ne postoji ni jedan paradoks?
Pitanje je vrlo zanimljivo i pokušaću da na njega odgovorim.
Današnja matematika je zasnovana na aksiomatskoj teoriji skupova (obično se uzima ZFC sistem), koja je zasnovana na predikatskom računu prvog reda, koji je zasnovan na svojim aksiomama i pravilima izvođenja. Dakle, imamo pravila izvođenja predikatskog računa prvog reda, aksiome predikatskog računa prvog reda i aksiome teorije skupova. Svi ostali pojmovi (osim skupa) su definisani preko pojma skupa.
Paradoks bi bio način da se po tim pravilima izvede neka formula i negacija te formule ili ekvivalentno da se dobije npr. formula 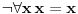 konačnom primenom pravila izvođenja predikatskog računa prvog reda na aksiome predikstskog računa prvog reda i teorije skupova. Takva (eventualna) mogućnost se zove protivrečnost teorije skupova.
Današnji matematičari (uz možda neke vrlo retke izuzetke) čvrsto veruju da je matematika neprotivrečna, odnosno da takvo izvođenje nije moguće, jer bi u protivnom menjali zasnivanje matematike. Međutim, tu neprotivrečnost niko nije dokazao prihvatljivim sredstvima. Štaviše, Kurt Gedel je dokazao da takav dokaz nije ni moguć istim takvim sredstvima, pa samim tim ni slabijim. Štaviše, dokazao je da je bilo kakav eventualni pokušaj zasnivanja matematike unapred osuđen ili na protivrečnost ili na nepotpunost uz nemogućnost dokazivosti neprotivrečnosti istim, odnosno slabijim sredstvima.
Kakve su onda perspektive za ispitivanje neprotivrečnosti zasnivanja matematike? Pa, matematičari svakoga dana dokazuju sve veći broj teorema. Ako bi paradoks postojao, postoji mogućnost da bi ga se neko setio. Međutim, to se nije desilo. To je jedna vrsta empirijske potvrde da paradoksa nema, ali naravno, ne i matematički dokaz (kakav po Gedelu nije ni moguć).
Sa druge strane, ako uz ZFC pretpostavimo postojanje slabo nedostižnih kardinala (WIC), odnosno pojačamo sredstva za dokazivanje, onda možemo da dokažemo (takvim, jačim sredstvima) da je ZFC neprotivrečan sistem.
Međutim, ko nam garantuje da je ta teorija neprotivrečna. Možda je ZFC protivrečna teorija, pa samim tim i ovakvo proširenje, pa pomenuti dokaz ne znači mnogo. Možda je pritom izvođenje protivrečnosti u ZFC toliko teško da ga se niko nije setio, ali bi onda u izvođenje kontradikcije u jačem sistemu ZFC+WIC bilo lakše. Ipak, ni izvođenja kontradikcije u tom sistemu se niko nije setio.
OK, možda je i to teško. Hipotezu o slabo nedostižnim kardinalima možemo zameniti još jačom hipotezom o postojanju jako nedostižnih kardinala (SIC), pa bi izvođenje protivrečnosti u sistemu ZFC+SIC bilo još lakše i bilo bi još lakše izvesti protivrečnost, odnosno bilo bi još izvesnije da se neko toga seti. Međutim, ni toga se niko nije setio.
Ako SIC zamenimo hipotezom o postojanju merljivih kardinala (MC), onda možemo dokazati da je ZFC+SIC neprotivrečna teorija. No, onda bi i ZFC+MC bila protivrečna teorija sa još lakšim načinom dolaženja do kontradikcije, jer smo pojačali sredstva, pa bi bilo još verovatnije da bi se neko setio takvog izvođenja kontradikcije. Međutim, ni toga se niko nije setio.
E, sad, postoje još veći tipovi kardinala u smislu da postojanje kardinala većeg tipa povlači da postoji ispod njega kardinal manjeg tipa, odakle sledi da se postojanje većeg povlači neprotivrečnost teorije skupova sa postojanjem manjeg kardinala. Postoji desetine tipova kardinala u toj hijerarhiji. Ni uz pretpostavku postojanja najvećih od njih niko još nije uspeo da izvede kontradikciju, što znači da je "običan" ZFC najverovatnije stvarno neprotivrečan.
U svakom slučaju, ako neko i pronađe protivrečnost unutar nekog od tih sistema, to neće biti nivo euklidske, pa ni neeuklidskih geometrija, jer je taj deo vrlo čvrsto zasnovan preko realnih brojeva, koji se na kraju zasnivaju preko prirodnih, već će se takva (eventualna) protivrečnost nalaziti u mnogo apstraktnijim slojevima. [ Nedeljko @ 01.05.2011. 19:23 ] @
Citat: igorpet: Ne, banovani su jer nisu znali da navedu primer a tvrdili su da paradoksi postoje
Ja sam naveo cak 2 primera, pa se nadam da nisam kandidat za banovanje :)
Ne, nisu banovani zbog toga, već iz drugih razloga. Primera radi, na toj temi se boxxter pozivao spisak referenci od kojih po svoj prilici nijednu nije ni nabavio, a nekmoli pročitao. [ igorpet @ 01.05.2011. 19:32 ] @
Nedeljko, o ovome sto si napisao ja ne mogu argumentovano da diskutujem jer moj nivo znanja nije na tom nivou (bolje reci mnogo je ispod).
Ali postoji odredjena samosvesnost koju mogu iskoristiti da barem pricam o ovome  (naravno, bez neke posebne argumentacije)
Ali ako je neko (tj. vise njih) posle 1.000 godina opovrglo npr. Euklidsku geometriju a bilo je ja mislim i drugih primera, ja bih ipak uzeo sa rezervom da danasnje teorije nece neko da opovrgne (ili bolje reci pronadje specijalne slucajeve kad ne vaze) za npr. 1.000 godina.
Nasa spoznaja o vremenu i prostoru i mestu u sirem kosmosu u kome zivimo nije jos uvek potpuno proucena i shvacena pa samim tim ja polazim od pretpostavke da se ne moze tvrditi da ovo sto je do sada otkriveno vazi uvek, svugde i u svim prilikama i ne vezano samo za nas prostor i vreme.
Ocigledno je da cetvrta dimenzija nije i poslednja dimenzija koja postoji, pa ce mozda ljudi kroz odredjeno vreme shvatiti (biti svesni) da u stvari zive u pet ili sest dimenzija i pitanje je da li ce sve ovo vaziti i tada.
Ja o ovome mogu diskutovati tek na laickom nivou, ali mislim da ljudi koji o ovome mogu govoriti na strucnom nivou mogu se prbrojati na prstima ruke.
[Ovu poruku je menjao igorpet dana 01.05.2011. u 20:55 GMT+1][ Nedeljko @ 01.05.2011. 20:23 ] @
Lepo je što razmišljaš o tome. Međutim, ne mogu da se složim sa tim da je euklidska geometrija opovrgnuta. Naprotiv, dokazana je njena neprotivrečnost. Druga je stvar što su ljudi shvatili da su pored nje moguće i druge geometrije. To ne znači da euklidska ne valja (naprotiv, i dan danas se uči i primenjuje), već samo da su moguće i druge.
Poređenje radi sa današnjom matematikom bih napravio ovako: U narednih 1000 godina će biti otkrivene nove važne matematičke teorije koje danas ne poznajemo, ali to ne znači da današnje ne valjaju.
[ poligonX @ 01.05.2011. 20:36 ] @
Citat: igorpet: Primer nije bio ubedljiv i osporen je kao paradoks :)
Ja sam dao jacu argumentaciju ;)
Gde je osporen kao paradoks? Ko je dao matematicku formulaciju Curryevog paradoksa? Mislio sam da je to otvoreno pitanje u matematici. Daj neki link.
Kao i u temi gde su prozvali one koji ispituju beta verzije windows-a, volim ponekad da stanem na stranu onih koji ulazu energiju u ovaj forum. Makar ih banovali, i prozivali da nemaju pojma, ili nazivali "zaludnim popovima koji krste jarice". [ igorpet @ 01.05.2011. 20:45 ] @
Citat: Nedeljko: Lepo je što razmišljaš o tome. Međutim, ne mogu da se složim sa tim da je euklidska geometrija opovrgnuta. Naprotiv, dokazana je njena neprotivrečnost. Druga je stvar što su ljudi shvatili da su pored nje moguće i druge geometrije. To ne znači da euklidska ne valja (naprotiv, i dan danas se uči i primenjuje), već samo da su moguće i druge.
Poređenje radi sa današnjom matematikom bih napravio ovako: U narednih 1000 godina će biti otkrivene nove važne matematičke teorije koje danas ne poznajemo, ali to ne znači da današnje ne valjaju.
Da, pogresno sam se izrazio, utvrdjeno je da ne vazi bas uvek i u svim prilikama (mislim da je peti postulat u pitanju).
A ja samo sumnjam da ce za 1.000 godina sadasnje teorije vaziti bez ogranicenja (mislim pojedine, ne bas sve).
To je ono sto ja mogu samo nagadjati, a to bas i nije neka matematika pa mozda je bolje da ovde stanem.
Mozda bi Fermijev paradoks bio nesto sto bi bilo analogno nekim mojim tvrdjenjima i sumnjama ( http://sr.wikipedia.org/sr-el/...%D0%B0%D0%B4%D0%BE%D0%BA%D1%81)
Mada neka moja licna ubedjenja su da pojedinci u rukama imaju veca znanja nego cime svet trenutno raspolaze i oni ne zele da ih stave na raspolaganju iz razlicitih razloga, ali ovo vec prevazilazi ovaj forum tako da samo iznosim svoje misljenje bez namere da se diskusija nastavi u ovom pravcu.
[ igorpet @ 01.05.2011. 20:50 ] @
Citat: poligonX: Gde je osporen kao paradoks? Ko je dao matematicku formulaciju Curryevog paradoksa? Mislio sam da je to otvoreno pitanje u matematici. Daj neki link...
Pa u istoj temi u Nedeljkovoj poruci ... http://www.elitesecurity.org/p2689782
Ne ulazim u istinitost iskaza, sam zakljucuj ...
A moj odgovor je bio vise saljive prirode ... nadam se da ste primetili  [ Nedeljko @ 01.05.2011. 21:31 ] @
Citat: igorpet: utvrdjeno je da ne vazi bas uvek i u svim prilikama (mislim da je peti postulat u pitanju).
A ja samo sumnjam da ce za 1.000 godina sadasnje teorije vaziti bez ogranicenja (mislim pojedine, ne bas sve).
Teorija, ako je aksiomatski zasnovana, počiva na nekim polaznim pojmovima i polaznim stavovima (aksiomama). Model jezika je svaka interpretacija polaznih pojmova. Model teorije je model njenog jezika u kome važe sve njene aksiome. U tom smislu su samo neki modeli jezika teorije ujedno i modeli teorije. Kada bi bili svi, aksiome bi bile nepotrebne (ako se ne radi o formalnom sistemu, već o "običnom" aksiomatskom sistemu). Aksiome su tu upravo da se iz svih modela jezika izdvoje neki. Kod praktičnih primena neke matematičke teorije imamo neku interpretaciju polaznih pojmova i moramo proveriti da li su pri toj interpretaciji zadovoljene aksiome te teorije. Upravo je to kriterijum primenljivosti te teorije u tom slučaju.
U tom smislu nijedna teorija ne važi bez ograničenja. Pogrešno je uverenje da teorija tvrdi da su njeni stavovi univerzalno tačni. Teorija zapravo garantuje da su svi stavovi teorije tačni u svakom modelu u kome važe sve aksiome te teorije, a aksiome se pre primene teorije moraju proveriti.
Primera radi, u teoriji izračunljivosti se obično razmatraju sistemi izračunljivosti ekvivalentni sa Tjuringovim mašinama, kojima računari kakve imamo samo približno odgovaraju jer za razliku od Tjuringovih mašina imaju konačnu memoriju. [ igorpet @ 01.05.2011. 22:20 ] @
Mislio sam na ovo:
Citat:
Zbir uglova u trouglu, zajedno sa pojmovima peti postulat, tj. shvatanjem paralelnosti, zatim ugao i odnos obima i prečnika kruga je jedna od najbezazlenijih tema iz geometrije, a sa druge strane to je jedno od najkrupnijih mesta celokupnog razvoja matematike.
U Euklidovim Elementima, knjiga I navodi se sledeća teorema
Teorema 32
U trouglu, ako se jedna stranica produži, tada je spoljašnji ugao jednak zbiru dva unutrašnja a suprotna ugla, a takođe zbir sva tri unutrašnja ugla trougla je jednak dva prava ugla.
Dokaz ove teoreme je posredno zavisan od V postulata, što za posledicu ima da u neeuklidskim geometrijama važi drugačija zakonitost. Zbir uglova u trouglu, u zavisnosti od vrste zakrivljenja prostora, može biti veći ili manji od dva prava ugla.
A sve ovo jer:
Citat:
Euklidska geometrija je u filozofskim i metafizičkim diskusijama vekovima navodjena kao primer savršene organizacije ljudskog mišljenja i njegove rigorozne formalizacije. Zasnovana na definicijama osnovnih objekata i pet aksioma, ili postulata, ona je pokazala kako se sve druge tvrdnje i teoreme geometrije mogu iz ovih formalno-logički izvesti. Rečju, Euklidska geometrija je navodjena kao ideal ljudske racionalnosti, destilovano razumevanje prostornih dimenzija i odnosa, a vrhunac i cilj svake naučne teorije bi trebao da bude njena finalna aksiomatizacija po uzoru na geometriju. (Ovo je postignuto u klasičnim disciplinama fizike - mehanika, termodinamika, elektrodinamika, itd., se mogu na ovaj način formulisati).
Mi osnovne geometrijske pojmove - tačka, prava, ravan i njihove odnose - predajemo djacima u osnovnoj školi, jer su ovi koncepti intuitivno jasni čak i deci koja su tek početnički pismena. Peti Euklidov postulat, na primer, kaže da, ako u ravni imamo pravu P, i tačku A van nje, onda se kroz tu tačku A može konstruisati samo jedna prava koja je sa pravom P paralelna. Ovo je intuitivno jasno i osnovcima.
Ili, kao drugi primer, tvrdnja da je najkraće rastojanje izmedju dve tačke prava linija se intuitivno razume kao "ako treba da predjem put odavde do tamo, onda mi je najkraće da idem pravo''.
Medjutim, upravo je Peti Euklidov postulat vekovima bio predmet preispitivanja (svi su izgledi da ni sam Euklid nije bio njime zadovoljan) jer se smatralo da je on tvrdnja koja se može iz ostala četiri postulata izvesti kao teorema i nije ga potrebno postavljati kao aksiom. Tek je tokom XIX veka pokazano da ovo nije tačno - Peti postulat je nezavistan od ostala četiri, i mi, barem formalno-logički gledano, imamo slobodu da ga formulišemo kako želimo. U tom smislu postoje tri mogućnosti: ako imamo pravu P, i tačku A van nje, onda se kroz tačku A može konstruisati:
1.) Samo jedna prava koja je sa pravom P paralelna
2.) Nijedna prava koja je sa pravom P paralelna, ili
3.) Više pravih (beskonačno mnogo njih, zapravo) koje su sa pravom P paralelne
Svaka od ovih opcija nam daje nezavistan aksiomatski sistem sa svim formalno-logičkim posledicama i teoremama koje unutar njega slede. Prva opcija nam daje standardnu Euklidsku geometriju, dok nam druge dve daju ne-Euklidske geometrije. Konkretno, druga opcija daje eliptičku geometriju (još zvanu i Riemannova geometrija), dok treća daje hiperboličku geometriju.
Mislim da smo se razumeli, tako da mozemo da stanemo ovde, ipak je tema o necem drugom
[Ovu poruku je menjao igorpet dana 02.05.2011. u 08:01 GMT+1][ poligonX @ 02.05.2011. 08:44 ] @
Pa taj Nedeljkov odgovor i jeste za salu i za smeh.
[ Sini82 @ 02.05.2011. 11:13 ] @
^
Kako kome.
[ petarm @ 02.05.2011. 11:28 ] @
Citat: poligonX: Pa taj Nedeljkov odgovor i jeste za salu i za smeh.
Ja nisam video neki smesan odgovor ovde. Prosto npr. recenica
Februar ima 28 dana.
nije iskaz. Iskaz je recenica koja moze imati samo jedno od dva svojstva
1) tacna je
2) netacna je
Februar moze imati i 29 dana, tako da boldovana recenica nije iskaz. [ Nedeljko @ 02.05.2011. 11:35 ] @
Iskazi su
Svaki februar u gregorijanskom kalendaru ima 28 dana
i
bar jedan februar u gregorijanskom kalendaru ima 28 dana.
Karijev paradoks je ilustracija jedne od nesavršenosti prirodnog jezika. U prirodnom jeziku ne možemo znati da je rečenica iskaz samo po konstrukciji rečenice, bez ulaženja u njeno značenje i analizu tog značenja, dok u formalnom matematičkom jeziku imamo garantovanu ispravnost formula već na osnovu njihove konstrukcije.
[ poligonX @ 02.05.2011. 14:24 ] @
Citat: petarm: Ja nisam video neki smesan odgovor ovde. Prosto npr. recenica
Februar ima 28 dana.
nije iskaz. Iskaz je recenica koja moze imati samo jedno od dva svojstva
1) tacna je
2) netacna je
Februar moze imati i 29 dana, tako da boldovana recenica nije iskaz. Citat: Nedeljko: Iskazi su
Svaki februar u gregorijanskom kalendaru ima 28 dana
i
bar jedan februar u gregorijanskom kalendaru ima 28 dana.
Karijev paradoks je ilustracija jedne od nesavršenosti prirodnog jezika. U prirodnom jeziku ne možemo znati da je rečenica iskaz samo po konstrukciji rečenice, bez ulaženja u njeno značenje i analizu tog značenja, dok u formalnom matematičkom jeziku imamo garantovanu ispravnost formula već na osnovu njihove konstrukcije.
Karijev paradoks je poznat i po tome sto je objasnjiv i deci iz osnovne skole.
-" Ako je ova recenica istinita, ova tri posta gore su pisana kineskim slovima "
_" Jel ti jasna ta recenica, jel u redu to da ako je ta recenica istinita, onda je i tvrdnja istinita?
-" Pa...da. Tacno je tako. To je istina.
- "Pa onda je ta recenica istinita?"
-" Pa...da. Jeste.
-"Ok. onda su oni gore postovi napisani kineskim slovima."
U cemu je stvar ovde? Ovde je stvar u tome sto ste vi sa lakocom resili otvoren problem u matematici oko koga se dvoume naucnici sa Stanforda, i iz celog sveta. Kad vam je predoceno koliko obimna literatura se bavi tim problemom, vi ste banovali korisnika pod izgovorom da ne razume sta tu pise, a s kilometra se videlo da je cilj bio samo da se ukaze na kompleksnost problema, i koliko naucnika se bavi sa tom materijom, koju ste vi resili u tri recenice. Verovatno smatrate da smo i mi deca, ili debili.
[ Sini82 @ 02.05.2011. 15:46 ] @
Citat: http://e.math.unizg.hr/math_e_...plavcic_skrtic_pavrlisak/index
Tokom istorije matematike, od antičkih vremena do danas, pojavljivali su se brojni problemi, kontradikcije i paradoksi, koji su doveli do preispitivanja tada prevladavajućih teorija, poticali traženje novih rješenja, te zaokupljajući misli tadašnjih matematičara ostavili svoj trag u istoriji matematike. Neki od njih samo su logički trikovi, neki su matematički tačne tvrdnje koje se intuitivno čine pogrešnima, a neki su ukazali na nepotpunosti u samim temeljima matematičkih teorija, zahtijevajući vrlo kreativno razmišljanje ne bi li ih se riješilo.
Uopšte paradoksom nazivamo tvrdnju ili grupu tvrdnji koje vode do kontradikcije ili situacije koja je u suprotnosti s intuicijom.
Rezultati pokazuju da je, kad je matematičko zaključivanje u kontradikciji s iskustvima iz stvarnog svijeta, najvjerojatnije je riječ o pogrešci. No, dok ne pronađemo pogrešku, suočeni smo s paradoksom. Citat:
poligonX:
Pa taj Nedeljkov odgovor i jeste za salu i za smeh.
Kako kome. Kakvi su tvoji odgovori na postavljenu temu? Paradoks paralelograma uopšte nije paradoks, već nečija greška u logičkom zaključivanju, koju smo otklonili. Kada bi tako pristupali rješavanju matematičkih problema, cijela matematika bi bila paradoks.
Ako želiš da raspravljaš o matematičkim paradoksima, otvori novu temu. [ poligonX @ 02.05.2011. 16:30 ] @
Ne, ne pada mi napamet da otvaram novu temu. Ona koja je bila otvorena o tome, zakljucana je, a korisnici su banovani.
Koliko treba da bude sujetan covek, i da samozadovoljno objavi resenje u par nebuloznih recenica, o problemu o kojem je napisano toliko kompleksne i strucne literature, od strane vrhunskih naucnika?
A i vas dvojica ste se tako fino slozili sa njim. Pravite nas majmunima da uzalud trosimo energiju, a za vas su otvorena pitanja u matematici vec resena. Zasto onda da gubimo vreme i da pricamo o tome, kada su vekovne rasprave o dualnosti istine za vas glupost.
Citat: Nedeljko@ Obzirom da nisu sve rečenice istinite, navedena rečenica se svodi na "Ja sam neistinita", a to nije iskaz jer nema tačno jednu od dve istinitosne vrednosti - tačno ili netačno. Opet nema nikakvog paradoksa. To je samo primer rečenice koja nije iskaz.
Genijalno.
Citat: petarm: Ja nisam video neki smesan odgovor ovde. Prosto npr. recenica
Februar ima 28 dana.
nije iskaz. Iskaz je recenica koja moze imati samo jedno od dva svojstva
1) tacna je
2) netacna je
Februar moze imati i 29 dana, tako da boldovana recenica nije iskaz.
Ovo je jos bolje.
I zavrsio bih sa ovim:
Citat: Nedeljko: Karijev paradoks je ilustracija jedne od nesavršenosti prirodnog jezika.
Bas ste kompleksno obradili problem.
Necu vise pisati o ovome. Sve je receno. [ Nedeljko @ 02.05.2011. 16:54 ] @
@poligonX
A, ti li si boxxter-u!
Citat: Nedeljko: No, pošto pretpostavljam da si prikupio i pročitao literaturu na koju se pozivaš, molim te da mi citiraš relevantne pasuse iz tih publikacija. Bez toga se ne može argumentovano tvrditi šta u toj literaturi piše, a šta ne.
Dakle, bilo je očigledno da je samo lupio link koji je izguglao i da nije nijednu od tih referenci nikada ni držao u ruci, a nekmoli čitao. Uostalom, to je bio obrazac njegovog ponašanja, što se može videti i ovde:
Citat: boxxter: Ostala resenja su interesantna primena Carpet-ove teoreme. Citat: Bojan Basic: Urnebesno. Dakle, ako je neko dosad i sumnjao da li ti samo prenosiš razne stvari koje iskopaš po Internetu — praveći se da znaš o čemu govoriš, a u stvari ne razumevajući ni najosnovnije pojmove — upravo si izuzetno efektno dokazao da je zaista tako. Ti teoremu koja se na engleskom zove Carpets Theorem, u prevodu teorema o tepisima, ovde nazivaš „Carpet-ova teorema“. Urnebesno. Citat: boxxter: He he. Naseli ste. Zato sam i namerno dodao taj post na kraju. Da vidim ko me najvise voli. [ poligonX @ 02.05.2011. 17:33 ] @
Nisam ja nikakav boxxter. Iskljucujem se. Uzivaj u svom samozadovoljstvu.
[ MarijaKg88 @ 02.05.2011. 17:37 ] @
Posto vidim da vodite zucnu raspavu,da li mi neko od vas moze reci da li je paradoks 2*2=5 to je matematicki ispravno a svi smo ucili drugacije?sto se tice paralelograma naravno da dijagonale nisu jednake,jel ni svi uglovi nisu jednaki.
[ pexi92 @ 02.05.2011. 17:44 ] @
Nek odgovori Nedeljko on sve zna najbolje
[ Nedeljko @ 02.05.2011. 18:26 ] @
Citat: MarijaKg88: 2*2=5 to je matematicki ispravno.
A zašto misliš da je matematički ispravno? [ kandorus @ 02.05.2011. 18:51 ] @
Možda je neka algebarska struktura u kojoj je 5 rezultat operacije * na (2,2).
[ MarijaKg88 @ 03.05.2011. 00:09 ] @
Prosto i jednostavno dokazuje se!
[ MarijaKg88 @ 03.05.2011. 00:21 ] @
Dokaz ide ovako:
neka je A=4,B=5 i C=1 tada imamo
C=B-A
kaka levu i desnu stranu pomnozimo sa B-A imamo
C(B-A)=(B-A)(B-A)
CB-CA=B^2-2AB+A^2
zatim oduzmemo A^2
CB-CA-A^2=B^2-2AB
zatim dodamo AB
CB-CA+AB-A^2=B^2-AB
zatim oduzmemo CB
AB-CA-A^2=B^2-AB-CB
odavde sa leve strane izvucemo A a sa desne B i imamo
A(B-C-A)=B(B-C-A)
skratimo sa B-C-A levu i desnu i dobijemo
A=B
odnosno
4=5 a to je 2*2=5
[ petarm @ 03.05.2011. 00:31 ] @
Zar ne primecujes da si delila nulom?
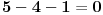 [ SrdjanR271 @ 03.05.2011. 02:21 ] @
@MarijaKG88
To ti je ovo:
a=0.
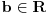
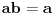
0=0.
Ili po tvom "dokazu" podelimo sa a=0 i dobijamo b=1.
Znači moze se dokazati da je svaki broj jednak 1, kad deliš nulom. [ Nedeljko @ 03.05.2011. 08:19 ] @
Samo jedna ispravka. Reč "dokazati" treba u tom kontekstu da bude pod znacima navoda.
[ MarijaKg88 @ 03.05.2011. 11:45 ] @
Sa navodimo ili bez totalno je nebitno,skracivane je dozvoljeno kad sve izmnozim dobijem 0=0 to je tacno ali ako mi je B-C-A=t imam pravo da skratim levu i desnu stranu,meni je lako bilo cudno kad sam ovo morala ucim za ispit.Mislim da i mi matematicari ucimo mnogo nepotrebnih stvari
[ the_tosic @ 03.05.2011. 11:52 ] @
Skracivanje je dozvoljeno kada to sto skracujes nije 0.
Ti si napisala 4*0 = 5*0 sto nista ne pokazuje!
Btw u 2. razredu osnovne skole se uci da deljenje nulom nije dozvoljeno.
[ pexi92 @ 03.05.2011. 12:08 ] @
Citat: MarijaKg88: .Mislim da i mi matematicari ucimo mnogo nepotrebnih stvari
XaXaXa
Neces se ti od matematike leba najesti [ Nedeljko @ 03.05.2011. 12:29 ] @
Citat: MarijaKg88: Mislim da i mi matematicari ucimo mnogo nepotrebnih stvari
Strašno je ako si ti sa takvim znanjem "matematičarka" a ne neko ko želi da nauči matematiku. [ petarm @ 03.05.2011. 12:47 ] @
Citat: MarijaKg88: Sa navodimo ili bez totalno je nebitno,skracivane je dozvoljeno kad sve izmnozim dobijem 0=0 to je tacno ali ako mi je B-C-A=t imam pravo da skratim levu i desnu stranu,meni je lako bilo cudno kad sam ovo morala ucim za ispit.Mislim da i mi matematicari ucimo mnogo nepotrebnih stvari
Na kojoj si ti godini studija? [ the_tosic @ 03.05.2011. 12:51 ] @
[ edisnp @ 03.05.2011. 13:00 ] @
A sta ako je to bila sala da je na trecoj.
[ igorpet @ 03.05.2011. 13:15 ] @
Citat: edisnp: A sta ako je to bila sala da je na trecoj.
A sta ako nije bila sala!? [ edisnp @ 03.05.2011. 13:21 ] @
E ako nije bila sala onda bruka.
[ kandorus @ 03.05.2011. 13:58 ] @
Čija bruka? Fakulteta i profesora?
Osim ako je prepisivala na ispitima.
MarijaKg88, jesi prepisivala?
[ edisnp @ 03.05.2011. 14:01 ] @
I fakulteta i nje same a sto se tice profesora niko nije savsren
kod svakog moze da se prepise tako da i ne treba sve svaljivati profesora.
Ozbiljno jesi li prepisevala na ispitima.
[ kandorus @ 03.05.2011. 14:21 ] @
Ja sam ubedjen da Marija ne prepisuje na ispitima. Ali nisam siguran da profesor ne sriče iz nekih beleški dok drži nastavu.
Pogledajte recimo sledeći primjer zadatka koji je riješio "profesor" (jedan od elitnih faksova):
Citat: x:U(a, 2a)
a) Odrediti ...
b) Odrediti ...
Rešenje:
a) f(x)=1/(3a)
...
b) f(x)=1/a
...
I gle čuda, dobije se da je ocena parametra i efikasna i postojana, baš kako se poželjeti može.
Xa Xa Xa. Statistika, nasa dika, što pozeliš to naslika... [ Nedeljko @ 03.05.2011. 15:40 ] @
Ja ne vidim šta je tu problem.
[ kandorus @ 03.05.2011. 16:08 ] @
Problem je što je prof. definisao funkciju gustine raspodele apsolutno neprekidne ravnomerne raspodele sa:
f(x)=1/(b-a), a <= x <= b
f(x)=0, inče.
Ali pri rešavanju zadatka do pola koristi f(x)=1/(b+a) a od pola koristi f(x)=1/(b-a). Nije u pitanju omaška jer se zadatak na nekoliko strana rešava pola ovako pola onako.
[ Nedeljko @ 04.05.2011. 08:47 ] @
Pa, ako su te polovine delovi pod a) i b), koji imaju yasebne formulacije, onda ništa nije čudno.
Kako uopšte glasi ceo zadatak?
[ kandorus @ 04.05.2011. 11:54 ] @
Za odredjivanje funkcije verodostojnosti može se poći od funkcije gustine raspodele. Data je slučajna promenljiva X sa uniformnom raspodelom X:U[a, 2a], a > 0. I čovek lepo ispiše:
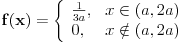
Što nije u skladu sa definicijom funkcije gustine raspodele.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|