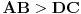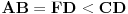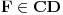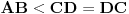[ nikolinv @ 02.05.2011. 21:13 ] @
| Dat je trapez ABCD, tačka E na pravoj AB tako da BE = DC = b, tačka F na pravoj CD takva da FD = AB = a. Tačka G je presek dijagonala, a H je presek dijagonale BD i duži EF. Obeležimo duži DG = x, HG = y i BH = z.  Trouglovi ABG i CDG su slični, pa važi: b/a = x/(y+z) Drugačije napisano: x = (b/a)(y+z) (*) Dalje, trouglovi BEH i DFH su takođe slični, pa imamo: b/a = z/(x+y) Ako izrazimo z dobijamo: z = (b/a)(x+y) (**) Odzimajući (*) i (**) zaključujemo: x-z = (b/a)(z-x) Ako sada podelimo poslednji izraz sa (z-x) i uzmemo absolutnu vrednost dobićemo: |b|/|a|=1 i konačno a = b. Ali ovo je moguće samo ako je četvorougao ABCD paralelogram. Da li je ovo paradoks ili nešto drugo? Ovde možete diskutovati o paradoksima generalno. Unapred hvala. |