Tačna (ne približna) kvadratuta kruga je nemoguća lenjirom i šestarom u konačnom broju koraka. To je dokazao Lindeman 1882. godine i ispravnost tog dokaza su proverili mnogi matematičari tokom ovih 129 godina. Pored ostalih, i moja malenkost se lično uverila u ispravnost toga. Stoga mi ne pada na pamet da čitam "dokaze" da to nije tačno. Isti odnos imaju svi ozbiljni matematičari (u koje sebe ne svrstavam, da se razumemo).

Druga je stvar npr. velika Fermaova teorema, koja je skoro četiri veka bila nedokazana, ali pri čemu niko nije u tom periodu ni dokazao da je netačna, pa su se pozabavili Vajlsovim dokazom.

Covek dokazao i objavio (u ne bas toliko strucnoj dnevnoj stampi) a ti i dalje ne verujes!!??

Ako neko dokaže ono što je dokazano da se ne može dokazati - onda se to zove paradoks
A za to već imamo otvorenu temu, pa ovo možes prebaciti tamo sa sve grafičkom metodom dokaza, nego malo mu slika sitna pa se dokaz ne vidi baš najjasnije, ali nećemo biti baš toliko sumnjičavi ... kad je ekskluzivnost u pitanju

Evo dokaza kvadrature kruga.
http://www.krug.in.rs/dokaz1.html

Na slici se iz aviona vidi da trouglovi CRD i CMO nisu slični, kao što se tvrdi pod 2).

Slični su kao pravougli sa zajedničkim oštrim uglom kod temena C.

No, ja i dalje ne vidim kako je on konstruisao sve one tačke na slici 2. Dok se to ne ispravi, nemam šta više da se udubljujem.

Hmmm,
pod 2. kaze da su trouglovi CRD i CMO slični
a pod 4. kaze da su i trouglovi CRB i CMO slični

E sad ... nista od paradoksa, osim ako u prvom slucaju ne podrazumeva geometriju Lobacevskog (ili cak neku noviju) a u drugom slucaju imamo samo Euklidsku geometriju ...
Izgleda da nisam dorastao da protumacim ovaj dokaz ...

Opet sličnost sledi iz toga što su ti trouglovi pravougli sa jednim zajedničkim oštrim uglom.

No, sama konstrukcija nije jasna i tu se ovakvi slučajevi zatvaraju.

Gdje sam ja gledao. Ciljano sam išao na to da nađem grešku, logiku sam skroz isključio.

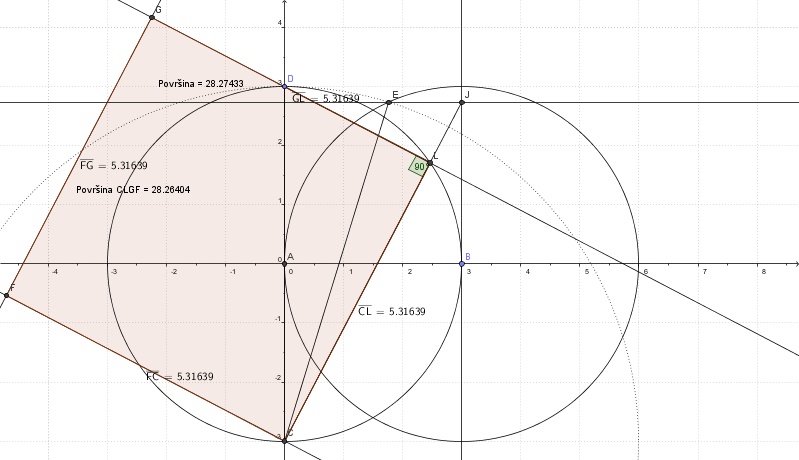
Ja sam na trenutak pomislo da ugao kod temena R (L) nije 90 stepeni, ali pogresih.
Ipak se povrsine ne slazu za malo, barem kako GeoGebra kaze.

imam problem da razlučim smerove dokazivanja, tj. izgleda mi da se pod pretpostavkom da je nešto jednako dolazi do zaključka da je to jednako, a ne poznajem dovoljno ni osobine zbira realnih brojeva da bih sve ispratila



_{[Ovu poruku je menjao berazorica dana 07.05.2011. u 23:27 GMT+1]}

Što se onog dokaza tiče, GeoGebra tvrdi da je u slučaju da je početni krug jediničnog poluprečnika, jedna od površina za koje se tvrdi da su jednake približno 7.1416, a druga približno 7.1419. Razlika je mala, ali ipak dovoljna da se ne može objasniti računskom greškom (GeoGebra računa sa 16 značajnih cifara).

Izveo sam proračun priložene konstrukcije u intervalnoj algebri, tako da je potpuno izvesno da se odstupanje ne može objasniti greškom računa.

,

.

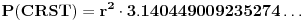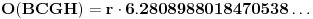Kad ja kažem da se ovakve stvari ne isplati gledati, ne veruje mi se.

Evo od sad ti verujemo.xD

Ima jedan veliki biser u računskom deku dokaza. Drugi red iza P1=P2 ima jedankost u obliku: A + B = C + D.
Kaže: pošto D nije jednako A, onda je D= B? Zašto? C i A nisu jednaki.