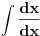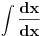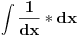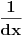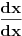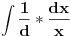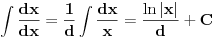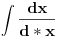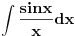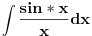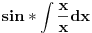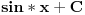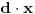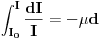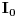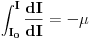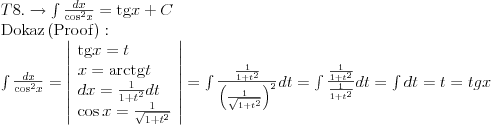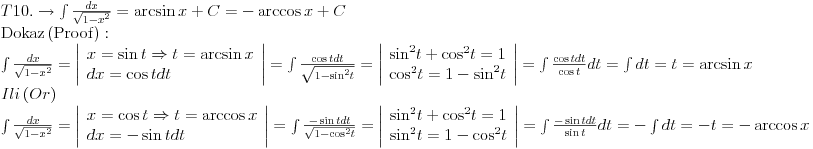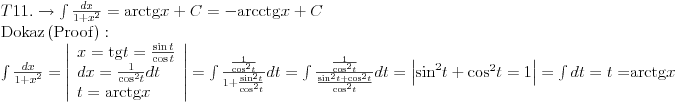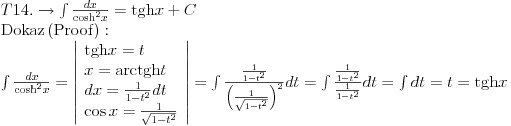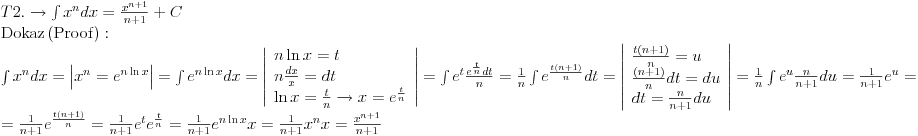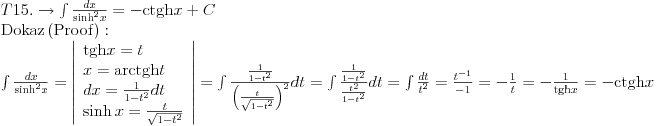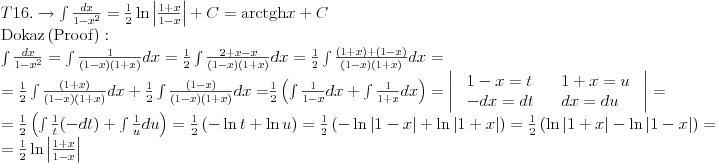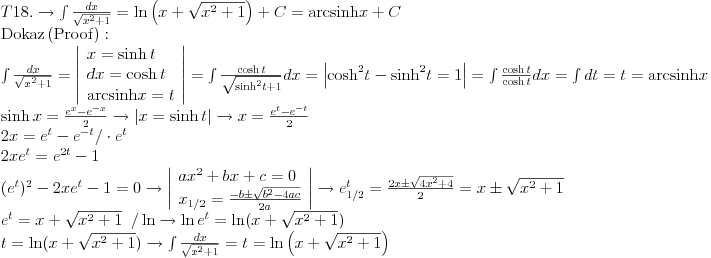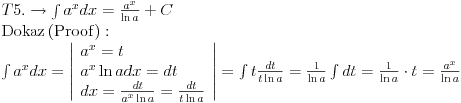[ igorpet @ 09.05.2011. 08:39 ] @
|
[ miki069 @ 09.05.2011. 09:03 ] @
[ igorpet @ 09.05.2011. 09:36 ] @
[ igorpet @ 09.05.2011. 10:01 ] @
Da, Nedeljko tako si i onu uradili i dali resenje ali sta je ovde 1/d, dato ovako samo?
Osim ako nisu mislili da je 1/d konstanta!? [Ovu poruku je menjao igorpet dana 09.05.2011. u 11:43 GMT+1] [ miki069 @ 09.05.2011. 11:10 ] @
[ igorpet @ 09.05.2011. 11:25 ] @
Slazem se, zato sam i pitao sta podrazumeva ovo d!
[ Nedeljko @ 09.05.2011. 11:33 ] @
[ igorpet @ 09.05.2011. 13:43 ] @
Ako su hteli da zbune, uspeli su
Ali mislim da bi bilo vise fer da su ovako napisali zadatak: 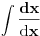 Ipad ona konstanta d je trebala biti data u formatu tekst a ne kao Math stil, no dobro. Mislim da ovakav trivijalan zadatak na ispitu ne bi uspelo da uradi velika vecina studenata, jer ono d asocira mnogo vise na diferencijal nego na konstantu, iako je formalno sve u redu sa zadatkom. [ petarm @ 09.05.2011. 13:46 ] @
[ igorpet @ 09.05.2011. 13:55 ] @
Citat: petarm: Fizicari rade nesto zbog cega se pojedini matematicari jeze... Pa izgleda da tu i lezi sustina odgovora na moje pitanje Mislim da je upravo ovo primer iz jedne knjige koju je pisao profesor fizike ... [ petarm @ 09.05.2011. 14:41 ] @
[ Bojan Basic @ 09.05.2011. 18:19 ] @
Citat: igorpet: Ako su hteli da zbune, uspeli su :) Ali mislim da bi bilo vise fer da su ovako napisali zadatak: 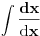 Ipad ona konstanta d je trebala biti data u formatu tekst a ne kao Math stil, no dobro. Nikad nisam video da se jednoslovne promenljive obeležavaju u tekstualnom formatu. Kada bih video 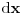 , nikad ne bih pomislio da to predstavlja proizvod dve promenljive, gde smo eto tako prvu obeležili regularom a drugu kurzivom. Naprotiv, ako bismo želeli da zadatak formulišemo na manje zbunjujuć način, verovatno bi trebalo upravo obratno: , nikad ne bih pomislio da to predstavlja proizvod dve promenljive, gde smo eto tako prvu obeležili regularom a drugu kurzivom. Naprotiv, ako bismo želeli da zadatak formulišemo na manje zbunjujuć način, verovatno bi trebalo upravo obratno: 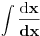 (obeležavanje diferencijala regularnim (obeležavanje diferencijala regularnim 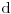 nije toliko neobično). nije toliko neobično).[ igorpet @ 09.05.2011. 18:35 ] @
Citat: Bojan Basic: Nikad nisam video da se jednoslovne promenljive obeležavaju u tekstualnom formatu. Kada bih video 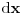 , nikad ne bih pomislio da to predstavlja proizvod dve promenljive, gde smo eto tako prvu obeležili regularom a drugu kurzivom. Naprotiv, ako bismo želeli da zadatak formulišemo na manje zbunjujuć način, verovatno bi trebalo upravo obratno: , nikad ne bih pomislio da to predstavlja proizvod dve promenljive, gde smo eto tako prvu obeležili regularom a drugu kurzivom. Naprotiv, ako bismo želeli da zadatak formulišemo na manje zbunjujuć način, verovatno bi trebalo upravo obratno: 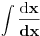 (obeležavanje diferencijala regularnim (obeležavanje diferencijala regularnim 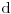 nije toliko neobično). nije toliko neobično).Pa kako god, ali da ih nekako razdvojimo ... kad su obe u kurzivu sansa da neko uoci d kao konstantu su prilicno male. Mozda je ovo dobra fora, da se isproba nacin na koji razmisljaju studenti ... bas me interesuje koji procenat bi se setio fore [ Nedeljko @ 09.05.2011. 18:50 ] @
Citat: petarm: Fizicari rade nesto zbog cega se pojedini matematicari jeze 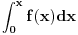 :) Ocito da se pojavljuju dva  -a koja nisu ista :) -a koja nisu ista :) Tesko je naci na primer neku knjigu iz nuklearne fizike gde nemate slucaj: 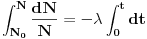 Ovo je zakon radioaktivnog raspada. Da, javljanja promenljive u granicama su slobodna (bar u smislu da nisu pod dejstvom integrala, već ničega ili eventualno nečega spolja), a javljanja promenljive po kojoj se vrši integracija pod integralom i u okviru diferencijala su vezana, tj. ograničena. Formalno je 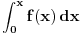 ispravno i potpuno ekvivalentno sa ispravno i potpuno ekvivalentno sa 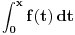 . Međutim, preporučljivo je izbegavati prvi način pisanja da bi se manje grešilo. Zato profesori to ne daju studentima - da bi manje padali na ispitima. Iz istog razloga se često zabranjuje primena Sarusovog ili Lopitalovog pravila, ondnosno formula . Međutim, preporučljivo je izbegavati prvi način pisanja da bi se manje grešilo. Zato profesori to ne daju studentima - da bi manje padali na ispitima. Iz istog razloga se često zabranjuje primena Sarusovog ili Lopitalovog pravila, ondnosno formula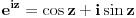 , ,koja važi u celoj kompleksnoj ravni, navodi se samo u realnom slučaju (jer liči na rastavljanje kompleksnog broja na realni i imaginarni deo, što je tačno samo u realnom slučaju). [ igorpet @ 11.05.2011. 07:14 ] @
Posto sam ovde poceo sa nekim elementarnim integralom mozda bi bilo interesantno pozabaviti se i tablicnim integralima.
Svojevremeno sam se bavio raznim vrstama integrala i dosao sam na ideju da resim tj. uradim tablicne integrale. To je bilo jednako zanimljivo kao i kad se rade neki daleko slozeniji. Zadatk sam postavio kao: Koristeci osnovna pravila i metode za integraljenje uraditi tablicne integrale. Tablica integrala je bila: 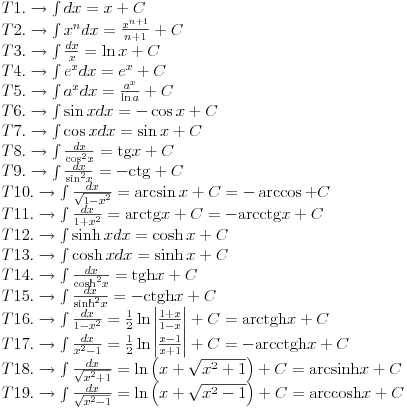 Uspeo sam sve ove da uradim, ali za pocetak sam uzeo da kao tablicni jedino koristim (na kraju sam se za T1 najvise i namucio 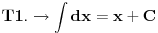 Nije bilo tesko uraditi: 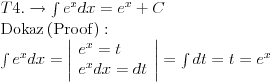 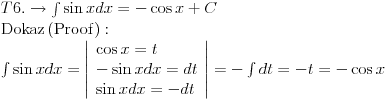 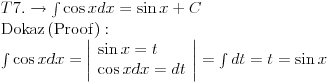 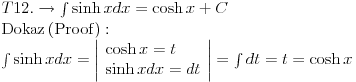 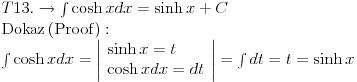 O ostalim u narednoj poruci... [ igorpet @ 11.05.2011. 08:40 ] @
[ miki069 @ 11.05.2011. 13:11 ] @
Zadnji je baš žongliranje.
Smena: (X^(n+1))/(n+1) = t X^n*dX = dt i u jednom redu se dobije rezultat. Svi predhodni su tako bili "urađeni". Krene se od rešenja i dokaže se izvodom da je tačno rešenje. Ništa tu nije rađeno, već je proveravano rešenje koje piše u rezultatu. Ajde probaj žonliranjem da uradiš T18 ili T19. [ igorpet @ 11.05.2011. 14:24 ] @
Citat: miki069: Zadnji je baš žongliranje. Smena: (X^(n+1))/(n+1) = t X^n*dX = dt i u jednom redu se dobije rezultat. Svi predhodni su tako bili "urađeni". Krene se od rešenja i dokaže se izvodom da je tačno rešenje. Ništa tu nije rađeno, već je proveravano rešenje koje piše u rezultatu. Ajde probaj žonliranjem da uradiš T18 ili T19. A ne, ne necemo da prejudiciramo resenje Idemo skroz zaobilaznim putem tj. putem kojim se redje ide [ igorpet @ 11.05.2011. 14:33 ] @
[ miki069 @ 11.05.2011. 17:43 ] @
T18 je urađen onako kako sam i rekao. Uzeo si da je t = rešenju i onda ga izdiferenciraš.
To što ga ti zoveš arcsinh(x) a ne ln(x+koren(x*x + 1)) je presipanje iz šupljeg u prazno. Nema tu ništa od žongliranja. Žongliranje bi bila smena tg(x) = t. [ pexi92 @ 12.05.2011. 02:09 ] @
Citat: Hm... Ti si ovde koristio T2 koji se resio koristeci T1, a sada koristis T2 da dokazes za T1... Ae probaj opet Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|