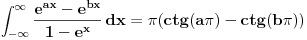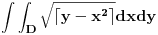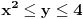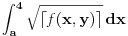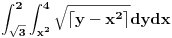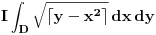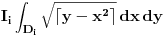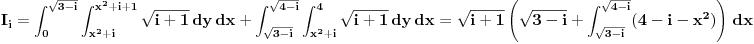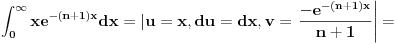[ SrdjanR271 @ 11.05.2011. 00:50 ] @
|
[ SrdjanR271 @ 11.05.2011. 02:24 ] @
[ Bojan Basic @ 11.05.2011. 02:57 ] @
[ miki069 @ 11.05.2011. 18:08 ] @
[ SrdjanR271 @ 11.05.2011. 18:39 ] @
[ SrdjanR271 @ 11.05.2011. 19:24 ] @
[ miki069 @ 11.05.2011. 19:52 ] @
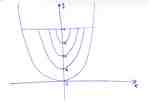
Srđane podintegralna funkcija ti je konstantna vrednost u određenim zonama.
Jel dobra ona moja podela na zone po Bojanovoj ideji? Ako jeste da ti izračunam. [ SrdjanR271 @ 11.05.2011. 19:54 ] @
Ja mislim da jeste dobra podela.
[ Nedeljko @ 11.05.2011. 20:00 ] @
[ miki069 @ 11.05.2011. 20:14 ] @
[ SrdjanR271 @ 11.05.2011. 20:50 ] @
Hvala svima, uradio sam sad konačno.
Citat: Nedeljko, mislim da ti u drugom dvostrukom integralu ne valja gornja granica za X. Nije fiksno 4 već koren(4-i). Ne valja. Sa granicom 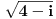 je sve ok. je sve ok.Hvala još jednom. Izvinite ako sam malo bio dosadan, ali nisam stvarno nikad radio integral sa floor ili ceil. [ Nedeljko @ 11.05.2011. 21:20 ] @
Hvala, kolega. Pazite na času. ;-) Ispravljeno.
[ SrdjanR271 @ 12.05.2011. 13:34 ] @
[ petarm @ 12.05.2011. 19:53 ] @
Mislim da ne može
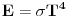 , gde je , gde je 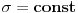 http://www.elitesecurity.org/t380828-0 Ono što možeš je da iskoristiš definiciju gama funkcije 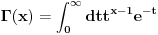 [Ovu poruku je menjao petarm dana 12.05.2011. u 21:04 GMT+1] Za 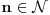 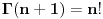 [Ovu poruku je menjao petarm dana 12.05.2011. u 21:05 GMT+1] [ SrdjanR271 @ 12.05.2011. 21:24 ] @
I ja mislim da ne može drugačije. Ali za ovaj gamma ne pomaže, jer je meni u imeniocu + .
A za taj tvoj može, zbog ovoga 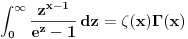 Ovaj integral sam prvi put video u Rimanovom radu iz 1859-e "On the Number of Prime Numbers less than a Given Quantity". Samo Riman tu piše 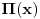 za gammu, mislim da je i Gaus tako pisao gammu. za gammu, mislim da je i Gaus tako pisao gammu. Razlika nije samo u slovu 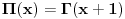 [ petarm @ 12.05.2011. 21:59 ] @
Citat: SrdjanR271: I ja mislim da ne može drugačije. Ali za ovaj gamma ne pomaže, jer je meni u imeniocu + . A za taj tvoj može, zbog ovoga 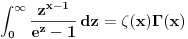 Ovaj integral sam prvi put video u Rimanovom radu iz 1859-e "On the Number of Prime Numbers less than a Given Quantity". Samo Riman tu piše 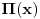 za gammu, mislim da je i Gaus tako pisao gammu. za gammu, mislim da je i Gaus tako pisao gammu. Razlika nije samo u slovu 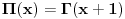 Citat: Mislio sam u ovom delu 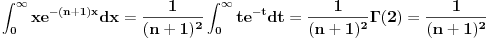 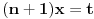 [ SrdjanR271 @ 12.05.2011. 22:09 ] @
Nisam te razumeo. To dosta skraćuje rešenje. Nisam razmišljao u tom pravcu.
Hvala za ideju! Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|