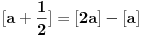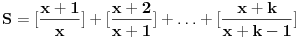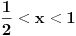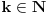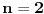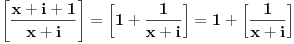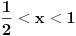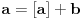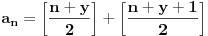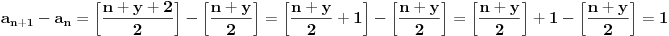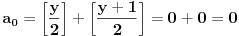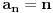Formiraj niz

Za je , a inače je za svako , odakle je . Prva jednakost je specijalan slučaj ove za .

Sa druge strane, u drugom zadatku je očigledno .

E, sad, izračunaj koliko je kada je i . Nije teško.

Sto se tice prvog zadatka nije mi bas najbolje jasno Nedeljkovo resenje evo ga neko lakse:..
Proveravanjem se dobija tacnost jednakosti.

Da, nisam napisao kako treba.

.

.

Pa drugi zadatak sam resio.
Al sto se tice prvog nikako nemogu da prekontam ovo sto je nedeljko napisao.
Mozda cu bit dosadan ali bi li mogao opet da mi objasnis prvi zadatak.

Neka je i . Dakle, .

.

,



Dakle, , pa je .