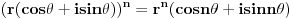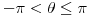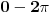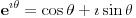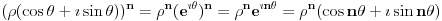[ Hari Haler @ 27.05.2011. 15:59 ] @
|
[ atomant @ 27.05.2011. 16:19 ] @
[ Sonec @ 27.05.2011. 18:19 ] @
Citat: Hari Haler: prilikom definisanja broja  , u jednom momentu imamo ovakvu nejednakost , u jednom momentu imamo ovakvu nejednakost 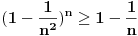 nakon čega slijedi ovo 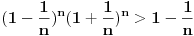 nije mi jasno zašto se prešlo na strogu nejednakost? Ne, to mora da je stamparska greska, nzm. odakle gledas dokaz,al treba da stoji vece jednako. To ti je sigurno, 100%, znam, imao sam kao potpitanje na usmenom dokaz broja e. Inace, to dobijas, pocetnu nejednakost, iz Bernulijeve nejednakosti, kada uvrstis da je 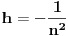 [Ovu poruku je menjao Sonec dana 27.05.2011. u 19:29 GMT+1] [Ovu poruku je menjao Sonec dana 27.05.2011. u 19:30 GMT+1] [ Nedeljko @ 27.05.2011. 20:07 ] @
[ Sini82 @ 28.05.2011. 10:56 ] @
http://alas.matf.bg.ac.rs/~brankica/sadrzaj/naslov5.html Imaš brojnu pravu (slika 1.), vidiš da 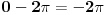 ne pripada intervalu ne pripada intervalu 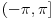 . .[ Hari Haler @ 28.05.2011. 11:25 ] @
Citat: atomant: Ovo drugo se zove Moavrova formula. Prakticna primena - stepenovanje kompleksnog broja. vjerovatno nema potrebe da ovo napominjem, ali toliko znam :) možda sam trebao to napisati, ali u svakom slučaju hvala na odgovoru. Citat: Sonec: Ne, to mora da je stamparska greska, nzm. odakle gledas dokaz,al treba da stoji vece jednako. To ti je sigurno, 100%, znam, imao sam kao potpitanje na usmenom dokaz broja e. odlično. već sam pomislio da ponovo previđam neku očiglednu-svima-jasnu stvar :) nisam mislio 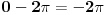 . mislio sam od 0 do . mislio sam od 0 do  . inače, ugao od . inače, ugao od 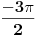 je veći od ugla od je veći od ugla od 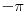 ? ?Citat: Nedeljko: 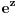 je samo oznaka za je samo oznaka za 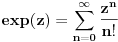 i ne mogu se koristiti osobine stepenovanja dok se ne dokažu. i ne mogu se koristiti osobine stepenovanja dok se ne dokažu.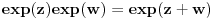 sledi iz teoreme o Košijevom množenju redova. Onda se indukcijom dokazuje da je sledi iz teoreme o Košijevom množenju redova. Onda se indukcijom dokazuje da je 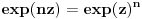 itd. itd.ovo je komentar na atomantov post? hvala svima na odgovorima. kao što sam već napisao imam još pitanja, pa ću vidjeti da ih postavim čim prije. pošto su neki dokazi u kojim sam naletio na nejasnoće malo duži, trebalo bi mi dosta vremena da ih iskucam pomoću latex-a. mogu li postaviti sliku sa rukom ispisanim dokazom? ne znam da li je to protiv pravila foruma? [ edisnp @ 28.05.2011. 12:45 ] @
Ja koliko znam bilo je takvih primera,gde su se zadaci postavljali
bez LateXa ,upravo koriscenjem slika,i raznih prikacenih fajlova. Tako ne bi trebalo to da ti predstavlja problem. [ Sini82 @ 30.05.2011. 11:17 ] @
@Hari Haler
3/2>1 tj. -3/2<-1; tako da je -3/2pi<-pi. [ Sonec @ 30.05.2011. 21:20 ] @
Citat: Ok.... Ovo je tacno, tj. ugao -3/2pi<-pi. Mada postupak nije dobar. Al jedno pitanje,koji je veci ugao, ugao od -4 pi ili ugao od -5pi ? Ja bih rekao da je veci ugao od -5pi, tj. ugao od 180 stepeni je veci od 0 stepeni..... Mada moze da se gleda da je -4 pi 360 stepeni.... Izvinjavam se ako gresim, malo sam u zurbi.... [ Hari Haler @ 30.05.2011. 21:50 ] @
Citat: izvini, pogrešno sam napisao. trebalo je biti -pi/2 i -pi. ja sam mislio da je -pi/2 veći pošto mu odgovara veći pozitivan ugao. ali ovaj tvoj način je logičniji :) ali kad se gleda na trigonometrijskoj kružnici, izgleda kao da je -pi veći. [ Nedeljko @ 30.05.2011. 22:25 ] @
Ugao je geometrijski pojam - skup oblast u ravni čija se granica sastoji od dve poluprave te ravni koje imaju zajedničko teme. Njegova mera u radijanima je uvek veća od nule a manja od
 . Sa druge strane, trigonometrijske funkcije su definisane na svim realnim, pa čak i svim kompleksnim brojevima, tako da nije greška pisati sinus ili kosinus od bilo kog realnog ili kompleksnog broja, s tim da to onda nije sinus ili kosinus ugla, nego realnog broja. . Sa druge strane, trigonometrijske funkcije su definisane na svim realnim, pa čak i svim kompleksnim brojevima, tako da nije greška pisati sinus ili kosinus od bilo kog realnog ili kompleksnog broja, s tim da to onda nije sinus ili kosinus ugla, nego realnog broja.[ Hari Haler @ 14.06.2011. 16:18 ] @
ako može neko da mi razjasni geometrijski smisao drugog izvoda.
[ Hari Haler @ 23.06.2011. 12:25 ] @
može li mi neko objasniti šta znači da je problem rješiv u polinomijalnom vremenu? naišao sam na ovo: ako postoji algoritam koji je u stanju da riješi bilo koju instancu I problema X veličine n (potrebna memorija) u p(n) koraka, gdje je p(n) polinom po promjenljivoj n, onda je X član skupa P problema rješivih u polinomijalnom vremenu.
takođe, šta bi značilo da je rješiv u eksponencijalnom vremenu? postavio sam još jedno pitanje u postu iznad, pa ako neko ima volje da odgovori i na to pitanje, ali ovo mi je daleko bitnije. svako dobro. [ edisnp @ 23.06.2011. 17:20 ] @
[ Hari Haler @ 23.06.2011. 17:47 ] @
edisnp pozdrav,
hvala na linkovima, ali pitanje o izvodima je bilo o geometrijskoj interpretaciji drugog izvoda. "U teoriji kompleksnosti, polinomijalno vreme se odnosi na vreme izračunavanja problema, gde vreme, m(n), nije veće od polinomijalne funkcije veličine problema, n. " ovo sam i ja našao, ali nije mi jasno šta znači da vrijeme izračunavanja nije veće od polinomijalne funkcije veličine problema? [ SrdjanR271 @ 23.06.2011. 17:57 ] @
Pogledaj ovo ako znaš engleski.
http://video.google.com/videoplay?docid=-1523750071462683553# [ edisnp @ 23.06.2011. 18:06 ] @
Samo da pitam nesto:Sta znaci kad je funkcija multiplikativna?.
Naisao sam na neke zadatke iz teorije brojeve sve ima samo ne ta definicija. [ SrdjanR271 @ 23.06.2011. 20:43 ] @
[ edisnp @ 23.06.2011. 20:46 ] @
Hvala na linku,ali bil mogo da neko svojim rjecima detaljno objasni,neko ko je imao iskustva sa nekim zadacima.
[ Hari Haler @ 24.06.2011. 10:02 ] @
Citat: SrdjanR271: Pogledaj ovo ako znaš engleski. http://video.google.com/videoplay?docid=-1523750071462683553# rijetki su koji ga danas ne znaju :) link je vezan za polinomijalno vrijeme? Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|